Predict trajectory of a bouncing ball

Question

Key Points:

• I have a default ball trajectory generated using some code(provided below). Lets name this trajectory Initial Trajectory.
• Next I have an actual ball whose trajectory I need to estimate.
• Now I need to improve the Initial Trajectory iteratively (to better represent actual ball trajectory) based on the coordinates of the actual ball as it moves through the environment.
• For example lets say after 5 units of time, I have 5 positions of where the actual ball has been through. Now I need to uses these 5 points and the Initial Trajectory to predict the future trajectory of the actual ball. I am expecting the actual trajectory to improve with time as more positions of the actual ball comes in.

Initial Trajectory Visualization:

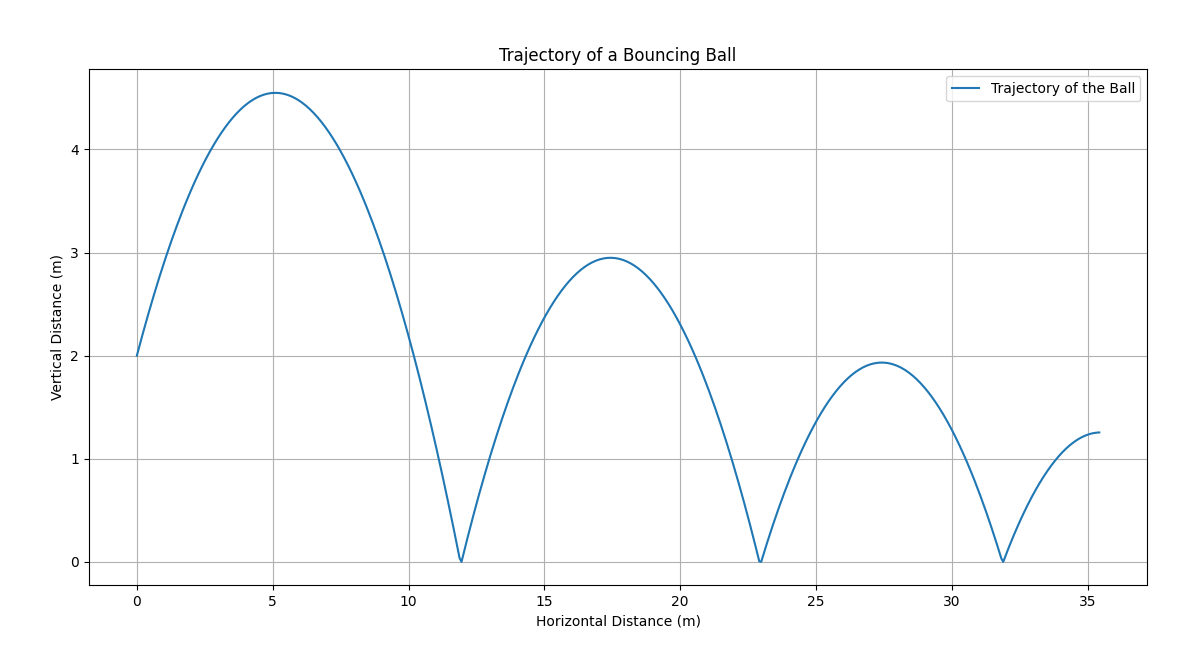
Initial Trajectory Code:

import numpy as np
import matplotlib.pyplot as plt

# Constants
g = 9.81  # gravity (m/s^2)
e = 0.8  # coefficient of restitution
theta = np.radians(45)  # launch angle (radians)
v0 = 10  # initial velocity (m/s)
x0, y0 = 0, 2  # initial position (m)
vx0 = v0 * np.cos(theta)  # initial horizontal velocity (m/s)
vy0 = v0 * np.sin(theta)  # initial vertical velocity (m/s)
t_step = 0.01  # time step for simulation (s)
t_max = 5  # max time for simulation (s)

# Initialize lists to store trajectory points
x_vals = [x0]
y_vals = [y0]

# Simulation loop
t = 0
x, y = x0, y0
vx, vy = vx0, vy0

while t < t_max:
    t += t_step
    x += vx * t_step
    y += vy * t_step - 0.5 * g * t_step ** 2
    vy -= g * t_step

    if y <= 0:  # Ball hits the ground
        y = 0
        vy = -e * vy

    x_vals.append(x)
    y_vals.append(y)

    if len(x_vals) > 1 and x_vals[-1] == x_vals[-2] and y_vals[-1] == y_vals[-2]:
        break  # Stop simulation if ball stops bouncing

# Plotting the trajectory
plt.figure(figsize=(10, 5))
plt.plot(x_vals, y_vals, label="Trajectory of the Ball")
plt.xlabel("Horizontal Distance (m)")
plt.ylabel("Vertical Distance (m)")
plt.title("Trajectory of a Bouncing Ball")
plt.legend()
plt.grid(True)
plt.show()

QUESTION:

• How can I combine a default bouncing ball trajectory and some coordinates of actual ball trajectory to predict the future trajectory of the actual ball.

NOTE:

• I am going with this method of trajectory approximation to better represent real world ball trajectory without having to fine tune complex parameters like energy loss on ball bounce, friction, type of floor, ball elasticity etc.

EDIT_1:

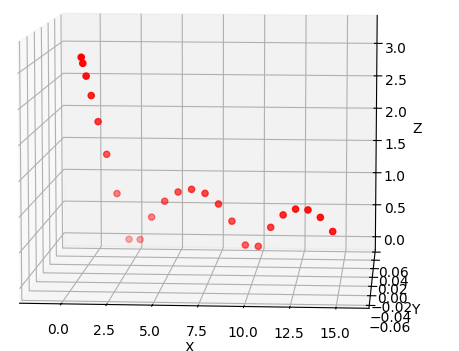
Actual Ball Trajectory Data:

X: [7.410000e-03 9.591000e-02 2.844100e-01 5.729100e-01 9.614100e-01
 1.449910e+00 2.038410e+00 2.726910e+00 3.373700e+00 4.040770e+00
 4.800040e+00 5.577610e+00 6.355180e+00 7.132750e+00 7.910320e+00
 8.687900e+00 9.465470e+00 1.020976e+01 1.092333e+01 1.163690e+01
 1.235047e+01 1.306404e+01 1.377762e+01 1.449119e+01]

Y: [2.991964 2.903274 2.716584 2.431894 2.049204 1.568514 0.989824 0.313134
 0.311512 0.646741 0.88397  1.0232   1.064429 1.007658 0.852887 0.600116
 0.249345 0.232557 0.516523 0.702488 0.790454 0.78042  0.672385 0.466351]

Graph(Actual Ball Trajectory):

• Note the ball being dropped from a certain height with some horizontal velocity.
• The graph is in 3D but I have simplified the data points to be 2D only (one of the axis is always zero) to keep the problem simpler.

EDIT_2:

I made use of scipy.optimize() with default method. Got the following output:

What I observed(looking at the image above) that there is some loss in horizontal velocity after bounce, which I was not considering. I thought there was only loss of vertical velocity. Here is the relevant code for the graph above:

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# actually y
act_x = np.array([0.019053200000000013, 0.08770320000000008, 0.1850550000000004, 0.2825550000000008, 0.38005500000000114, 0.4775550000000015, 0.5750549999999806, 0.6725549999999532, 0.7700549999999258, 0.8675549999998984, 0.965054999999871, 1.0625549999998436, 1.1600549999998162, 1.2575549999997888, 1.3550549999997614, 1.452554999999734, 1.5500549999997066, 1.6475549999996792, 1.7450549999996519, 1.8425549999996245, 1.940054999999597, 2.0375549999996125, 2.1234107142854164, 2.193053571428365, 2.2626964285713136, 2.332339285714262, 2.401982142857211, 2.4716250000001594, 2.541267857143108, 2.6109107142860566, 2.680553571429005, 2.750196428571954, 2.8198392857149024, 2.889482142857851, 2.9591250000007996, 3.028767857143748, 3.098410714286697, 3.1680535714296454, 3.237696428572594, 3.3073392857155426, 3.376982142858491, 3.44662500000144, 3.5162678571443884, 3.585910714287337, 3.6555535714302856, 3.725196428573234, 3.794839285716183, 3.8644821428591314, 3.93412500000208, 4.003767857145029, 4.073410714287977, 4.143053571430926, 4.212696428573874, 4.282339285716823, 4.351982142859772, 4.42162500000272, 4.491267857145669, 4.560910714288617, 4.630553571431566, 4.700196428574515, 4.769839285717463, 4.839482142860412, 4.90912500000336, 4.978767857146309, 5.048410714289258, 5.118053571432206, 5.187696428575155, 5.257339285718103, 5.326982142861052, 5.396625000004001, 5.466267857146949, 5.535910714289898, 5.605553571432846, 5.675196428575795, 5.744839285718744, 5.814482142861692, 5.884125000004641, 5.953767857147589, 6.023410714290538, 6.093053571433487, 6.162696428576435, 6.232339285719384, 6.301982142862332, 6.371625000005281, 6.44126785714823, 6.510910714291178, 6.580553571434127, 6.650196428577075, 6.719839285720024, 6.789482142862973, 6.859125000005921, 6.92876785714887, 6.998410714291818, 7.068053571434767, 7.137696428577716, 7.207339285720664, 7.276982142863613, 7.346625000006561, 7.41626785714951, 7.485910714292459, 7.555553571435407, 7.625196428578356, 7.694839285721304, 7.764482142864253])
# actually z
act_y = np.array([1.0379079699999998, 1.1754534700000003, 1.3602534700000006, 1.5209239699999955, 1.6570944699999859, 1.7687649699999706, 1.8559354699999533, 1.9186059699999365, 1.95677646999992, 1.970446969999904, 1.9596174699998887, 1.9242879699998736, 1.8644584699998585, 1.7801289699998444, 1.6712994699998283, 1.537969969999807, 1.3801404699997812, 1.19781096999975, 0.9909814699997134, 0.7596519699996719, 0.5038224699996257, 0.22349296999957416, 0.13930352847394978, 0.3499050645343172, 0.5360066005946793, 0.6976081366550367, 0.8347096727153887, 0.9473112087757359, 1.0354127448360804, 1.0990142808964258, 1.1381158169567716, 1.1527173530171173, 1.1428188890774638, 1.1084204251378103, 1.0495219611981568, 0.9661234972585043, 0.8582250333188504, 0.7258265693791917, 0.5689281054395274, 0.3875296414998584, 0.18163117756018424, 0.11887053865291446, 0.2798887215524012, 0.41640690445188283, 0.5284250873513592, 0.6159432702508338, 0.6789614531503088, 0.7174796360497837, 0.7314978189492595, 0.7210160018487353, 0.6860341847482112, 0.6265523676476875, 0.5425705505471646, 0.4340887334466397, 0.3011069163461103, 0.14362509924557573, 0.10758844178113687, 0.2208353837910192, 0.309582325800899, 0.37382926781077935, 0.41357620982065996, 0.42882315183054115, 0.4195700938404224, 0.385817035850304, 0.3275639778601862, 0.24481091987006875, 0.13755786187995, 0.07905142871570557, 0.1646809455657065, 0.22581046241570793, 0.2624399792657099, 0.2745694961157122, 0.26219901296571463, 0.2253285298157173, 0.16395804666572056, 0.07808756351572432, 0.09996825173824968, 0.1511630228129375, 0.17785779388762588, 0.1800525649623144, 0.15774733603700322, 0.11094210711169239, 0.05563702598852237, 0.09995862508974714, 0.11978022419097237, 0.1151018232921977, 0.08592342239342333, 0.06022248147389577, 0.08484848858531084, 0.0849744956967261, 0.06060050280814157, 0.06605277311641561, 0.06792022730639775, 0.05243051383233173, 0.060240252169206004, 0.0532114047328211, 0.05285089806699147, 0.052793140813351076, 0.05130362411928389, 0.05057861286791727, 0.049998536419320685, 0.049997973905616416, 0.049997920093917625, 0.049997920094010155])

def get_initial_trajectory(e_1=0.8):
    # Constants
    g = 9.81  # gravity (m/s^2)
    e = e_1 #0.8  # coefficient of restitution
    theta = np.radians(45)  # launch angle (radians)
    v0 = 10  # initial velocity (m/s)
    x0, y0 = 0, 1  # initial position (m)
    #vx0 = (v0 * np.cos(theta))*-1  # initial horizontal velocity (m/s)
    #vy0 = v0 * np.sin(theta)  # initial vertical velocity (m/s)

    vx0 = 1.95
    vy0 = 4.4

    t_step = 0.01  # time step for simulation (s)
    t_max = 5  # max time for simulation (s)

    # Initialize lists to store trajectory points
    x_vals = [x0]
    y_vals = [y0]

    # Simulation loop
    t = 0
    x, y = x0, y0
    vx, vy = vx0, vy0

    while t < t_max:
        t += t_step
        x += vx * t_step
        y += vy * t_step - 0.5 * g * t_step ** 2
        vy -= g * t_step

        if y <= 0:  # Ball hits the ground
            y = 0
            vy = -e * vy

        x_vals.append(x)
        y_vals.append(y[0] if isinstance(y, np.ndarray) else y )

        if len(x_vals) > 1 and x_vals[-1] == x_vals[-2] and y_vals[-1] == y_vals[-2]:
            break  # Stop simulation if ball stops bouncing

    return x_vals, y_vals

def cost_function(params):
    e_1 = params
    x_vals, y_vals = get_initial_trajectory(e_1)

    print(x_vals)
    print(y_vals)
    y_temp = np.interp(act_x, x_vals, y_vals)

    return np.sum((act_y - y_temp)**2)


param = np.array([0.8])

output = minimize(cost_function, param, bounds=[(None, None)])

print("Tuned Coefficient of Restitution: ", output)

x_vals, y_vals = get_initial_trajectory(0.8)
x_vals_new, y_vals_new = get_initial_trajectory(7.207e-01)

# Plotting the trajectory
plt.figure(figsize=(10, 5))
plt.plot(x_vals, y_vals, label="Initial Trajectory")
plt.scatter(act_x, act_y, color='r', label='Observed')
plt.plot(x_vals_new, y_vals_new, label="Output Trajectory", color="orange")
plt.xlabel("Horizontal Distance (m)")
plt.ylabel("Vertical Distance (m)")
plt.title("Trajectory of a Bouncing Ball")
plt.legend()
plt.grid(True)
plt.show()

To correct this, I added a parameter q for loss in horizontal velocity. And made some changes in code after bounce:

Before Code:

if y <= 0:  # Ball hits the ground
    y = 0
    vy = -e * vy

After Code:

if y <= 0:  # Ball hits the ground
    y = 0
    vy = -e * vy
    vx = vx * q    # Added

This change seems to improve the output(The red and orange line seems more aligned especially for the first 2 bumps):

Here is the updated code:

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# actually y
act_x = np.array([0.019053200000000013, 0.08770320000000008, 0.1850550000000004, 0.2825550000000008, 0.38005500000000114, 0.4775550000000015, 0.5750549999999806, 0.6725549999999532, 0.7700549999999258, 0.8675549999998984, 0.965054999999871, 1.0625549999998436, 1.1600549999998162, 1.2575549999997888, 1.3550549999997614, 1.452554999999734, 1.5500549999997066, 1.6475549999996792, 1.7450549999996519, 1.8425549999996245, 1.940054999999597, 2.0375549999996125, 2.1234107142854164, 2.193053571428365, 2.2626964285713136, 2.332339285714262, 2.401982142857211, 2.4716250000001594, 2.541267857143108, 2.6109107142860566, 2.680553571429005, 2.750196428571954, 2.8198392857149024, 2.889482142857851, 2.9591250000007996, 3.028767857143748, 3.098410714286697, 3.1680535714296454, 3.237696428572594, 3.3073392857155426, 3.376982142858491, 3.44662500000144, 3.5162678571443884, 3.585910714287337, 3.6555535714302856, 3.725196428573234, 3.794839285716183, 3.8644821428591314, 3.93412500000208, 4.003767857145029, 4.073410714287977, 4.143053571430926, 4.212696428573874, 4.282339285716823, 4.351982142859772, 4.42162500000272, 4.491267857145669, 4.560910714288617, 4.630553571431566, 4.700196428574515, 4.769839285717463, 4.839482142860412, 4.90912500000336, 4.978767857146309, 5.048410714289258, 5.118053571432206, 5.187696428575155, 5.257339285718103, 5.326982142861052, 5.396625000004001, 5.466267857146949, 5.535910714289898, 5.605553571432846, 5.675196428575795, 5.744839285718744, 5.814482142861692, 5.884125000004641, 5.953767857147589, 6.023410714290538, 6.093053571433487, 6.162696428576435, 6.232339285719384, 6.301982142862332, 6.371625000005281, 6.44126785714823, 6.510910714291178, 6.580553571434127, 6.650196428577075, 6.719839285720024, 6.789482142862973, 6.859125000005921, 6.92876785714887, 6.998410714291818, 7.068053571434767, 7.137696428577716, 7.207339285720664, 7.276982142863613, 7.346625000006561, 7.41626785714951, 7.485910714292459, 7.555553571435407, 7.625196428578356, 7.694839285721304, 7.764482142864253])
# actually z
act_y = np.array([1.0379079699999998, 1.1754534700000003, 1.3602534700000006, 1.5209239699999955, 1.6570944699999859, 1.7687649699999706, 1.8559354699999533, 1.9186059699999365, 1.95677646999992, 1.970446969999904, 1.9596174699998887, 1.9242879699998736, 1.8644584699998585, 1.7801289699998444, 1.6712994699998283, 1.537969969999807, 1.3801404699997812, 1.19781096999975, 0.9909814699997134, 0.7596519699996719, 0.5038224699996257, 0.22349296999957416, 0.13930352847394978, 0.3499050645343172, 0.5360066005946793, 0.6976081366550367, 0.8347096727153887, 0.9473112087757359, 1.0354127448360804, 1.0990142808964258, 1.1381158169567716, 1.1527173530171173, 1.1428188890774638, 1.1084204251378103, 1.0495219611981568, 0.9661234972585043, 0.8582250333188504, 0.7258265693791917, 0.5689281054395274, 0.3875296414998584, 0.18163117756018424, 0.11887053865291446, 0.2798887215524012, 0.41640690445188283, 0.5284250873513592, 0.6159432702508338, 0.6789614531503088, 0.7174796360497837, 0.7314978189492595, 0.7210160018487353, 0.6860341847482112, 0.6265523676476875, 0.5425705505471646, 0.4340887334466397, 0.3011069163461103, 0.14362509924557573, 0.10758844178113687, 0.2208353837910192, 0.309582325800899, 0.37382926781077935, 0.41357620982065996, 0.42882315183054115, 0.4195700938404224, 0.385817035850304, 0.3275639778601862, 0.24481091987006875, 0.13755786187995, 0.07905142871570557, 0.1646809455657065, 0.22581046241570793, 0.2624399792657099, 0.2745694961157122, 0.26219901296571463, 0.2253285298157173, 0.16395804666572056, 0.07808756351572432, 0.09996825173824968, 0.1511630228129375, 0.17785779388762588, 0.1800525649623144, 0.15774733603700322, 0.11094210711169239, 0.05563702598852237, 0.09995862508974714, 0.11978022419097237, 0.1151018232921977, 0.08592342239342333, 0.06022248147389577, 0.08484848858531084, 0.0849744956967261, 0.06060050280814157, 0.06605277311641561, 0.06792022730639775, 0.05243051383233173, 0.060240252169206004, 0.0532114047328211, 0.05285089806699147, 0.052793140813351076, 0.05130362411928389, 0.05057861286791727, 0.049998536419320685, 0.049997973905616416, 0.049997920093917625, 0.049997920094010155])

def get_initial_trajectory(e_1=0.8, q_1=1):
    # Constants
    g = 9.81  # gravity (m/s^2)
    e = e_1 #0.8  # coefficient of restitution
    q = q_1     # Horizontal velocity coefficient
    theta = np.radians(45)  # launch angle (radians)
    v0 = 10  # initial velocity (m/s)
    x0, y0 = 0, 1  # initial position (m)
    #vx0 = (v0 * np.cos(theta))*-1  # initial horizontal velocity (m/s)
    #vy0 = v0 * np.sin(theta)  # initial vertical velocity (m/s)

    vx0 = 1.95
    vy0 = 4.4

    t_step = 0.01  # time step for simulation (s)
    t_max = 5  # max time for simulation (s)

    # Initialize lists to store trajectory points
    x_vals = [x0]
    y_vals = [y0]

    # Simulation loop
    t = 0
    x, y = x0, y0
    vx, vy = vx0, vy0

    while t < t_max:
        t += t_step
        x += vx * t_step
        y += vy * t_step - 0.5 * g * t_step ** 2
        vy -= g * t_step

        if y <= 0:  # Ball hits the ground
            y = 0
            vy = -e * vy

            vx = vx * q    # Added

        x_vals.append(x)
        y_vals.append(y[0] if isinstance(y, np.ndarray) else y )

        if len(x_vals) > 1 and x_vals[-1] == x_vals[-2] and y_vals[-1] == y_vals[-2]:
            break  # Stop simulation if ball stops bouncing

    return x_vals, y_vals

def cost_function(params):
    e_1, q_1 = params
    x_vals, y_vals = get_initial_trajectory(e_1, q_1)

    print(x_vals)
    print(y_vals)
    y_temp = np.interp(act_x, x_vals, y_vals)

    return np.sum((act_y - y_temp)**2)


param = np.array([0.8, 1])

output = minimize(cost_function, param, bounds=[(None, None)])

print("Tuned Coefficient of Restitution: ", output)

x_vals, y_vals = get_initial_trajectory(0.8, 1)
x_vals_new, y_vals_new = get_initial_trajectory(output.x[0], output.x[1])

# Plotting the trajectory
plt.figure(figsize=(10, 5))
plt.plot(x_vals, y_vals, label="Initial Trajectory")
plt.scatter(act_x, act_y, color='r', label='Actual Ball Trajectory')
plt.plot(x_vals_new, y_vals_new, label="Output Trajectory", color="orange")
plt.xlabel("Horizontal Distance (m)")
plt.ylabel("Vertical Distance (m)")
plt.title("Trajectory of a Bouncing Ball")
plt.legend()
plt.grid(True)
plt.show()

But the results are not perfect. The orange line does not completely overlaps the red dotted line.
Now I am completely lost of what to do next:

• Shall I use better optimizer (like what @Bill mentioned GEKKO, CasADi, Pyomo)?
• Or change the formula to add more parameters(as it helped in the last change)?

Vocative

you need to change the parameter values until the trajectory matches the actual ball points. You can do an intensive grid search looking for all combinations or a smarter approach like gradient descent – Selfabsorption

Do you have data for a measured trajectory? If so please post it here. If not it will be difficult to demonstrate a realistic solution. – Miticide

@Miticide Have updated the question. Note the data is generated using a simulator(Gazebo). – Vocative

The data show a constant y-offset of about 0.05. Why? – Miticide

What are the sample times of the actual ball trajectory (X, Y)? – Kazue

@Miticide Between which colored lines? If you are talking about the second last image between orange and red line then it might be because the optimizer is not working well. – Vocative

@Kazue I have used new ball trajectory in the EDIT_2 section. The frequency of data is 20 Hertz(20 times a second as ball moves). Earlier it was 10 Hertz. – Vocative

Answer 1

What you are trying to do is known as system identification in the academic literature. Sys Id is a method used to identify the parameters of dynamical systems models from trajectory data.

Once you have a good model fitted to the data, you can then predict the future trajectory of the ball (see also @el_pazzu's answer for using a Kalman filter although this might be tricky with your non-linear system).

Your system is non-linear due to the bouncing behaviour so you will have to set up a non-linear optimization problem and try to solve it for the parameters of your model.

The simplest method of system identification is the single-shooting method which involves simulating an entire trajectory and then comparing it to the outputs from the true system.

This is the prediction error method, which usually involves minimizing the squared-errors between the output trajectory predicted by the model and the data.

Hope that helps. There are many resources online to do this. There are some curated tutorials here:

• https://resourcium.org/topic/system-identification

Also, MATLAB software has a comprehensive set of tools to help you do it.

But I would try solving it using scipy.optimize first. If that doesn't work you may need to consider more advanced non-linear optimization algorithms (see for example, GEKKO, CasADi, Pyomo

Hope that helps. Good luck, it's a very interesting problem...

Kazue

You might also want to check out this tutorial: meco-software.pages.gitlab.kuleuven.be/rockit/examples/… – Kazue

* After going through matlab videos, i thought i need to apply differential equation. But once i understood the concept of differential equation, I think i can directly use the horizontal and vertical displacement equations(that i used in the code). Could you just confirm it? * I thought of applying gradient descent but it is not directly available in scipy. Would it be better to implement gradient descent or use any other optimizer? Could you suggest any optimizer? I do not have much experience with it. – Vocative

Your difference equations in lines 38 and 39 are fine. These are the discrete-time Euler approximation of the (continuous-time) differential equations of the system. One drawback of discretizing time is that the ball contacts with the ground will not occur exactly at the sample times. But you still should get an approximate solution and working in discrete time is much simpler. – Kazue

I already recommended three optimization suites that include non-linear optimization algorithms such as IPOPT. These use higher order gradient descent algorithms and allow you to impose constraints. Did you try any of them? – Kazue

No i have not used any of these. I tried all algorithms of scipy.optimize and none of them seems to work good. I will try IPOPT. – Vocative

Answer 2

Have you tried using a Kalman filter:

import numpy as np
import matplotlib.pyplot as plt

g = 9.81
e = 0.8
t_step = 0.01

# Initial actual ball trajectory data
actual_x = np.array([7.410000e-03, 9.591000e-02, 2.844100e-01, 5.729100e-01, 9.614100e-01,
                     1.449910e+00, 2.038410e+00, 2.726910e+00, 3.373700e+00, 4.040770e+00,
                     4.800040e+00, 5.577610e+00, 6.355180e+00, 7.132750e+00, 7.910320e+00,
                     8.687900e+00, 9.465470e+00, 1.020976e+01, 1.092333e+01, 1.163690e+01,
                     1.235047e+01, 1.306404e+01, 1.377762e+01, 1.449119e+01])
actual_y = np.array([2.991964, 2.903274, 2.716584, 2.431894, 2.049204, 1.568514, 0.989824, 0.313134,
                     0.311512, 0.646741, 0.88397, 1.0232, 1.064429, 1.007658, 0.852887, 0.600116,
                     0.249345, 0.232557, 0.516523, 0.702488, 0.790454, 0.78042, 0.672385, 0.466351])

# Initial state (position & velocity)
initial_state = np.array([0, 2, 10 * np.cos(np.radians(45)), 10 * np.sin(np.radians(45))])  # [x, y, vx, vy]

# State transition matrix
dt = t_step
F = np.array([[1, 0, dt, 0],
              [0, 1, 0, dt],
              [0, 0, 1, 0],
              [0, 0, 0, 1]])

# Measurement matrix
H = np.array([[1, 0, 0, 0],
              [0, 1, 0, 0]])

# Process noise covariance
Q = np.eye(4) * 0.001

# Measure noise covariance
R = np.eye(2) * 0.01

# Initial covariance matrix
P = np.eye(4)

def predict(state, P):
    state_pred = F @ state
    P_pred = F @ P @ F.T + Q
    return state_pred, P_pred

def update(state_pred, P_pred, measurement):
    y = measurement - H @ state_pred
    S = H @ P_pred @ H.T + R
    K = P_pred @ H.T @ np.linalg.inv(S)
    state_upd = state_pred + K @ y
    P_upd = (np.eye(4) - K @ H) @ P_pred
    return state_upd, P_upd

# Initialize state & covariance
state = initial_state
trajectory = [state[:2]]
time = 0

# Do Kalman filtering with actual measurements
for i in range(len(actual_x)):
    # Predict
    state_pred, P_pred = predict(state, P)

    # Measure
    measurement = np.array([actual_x[i], actual_y[i]])

    # Update
    state, P = update(state_pred, P_pred, measurement)

    # Save
    trajectory.append(state[:2])

# Convert trajectory to np array for plotting
trajectory = np.array(trajectory)

# Plot trajectory
plt.figure(figsize=(10, 5))
plt.plot(trajectory[:, 0], trajectory[:, 1], label="Predicted trajectory", color='r')
plt.scatter(actual_x, actual_y, label="Actual trajectory", color='b')
plt.xlabel("Horizontal distance")
plt.ylabel("Vertical distance")
plt.title("Trajectory of bouncing ball with Kalman filter")
plt.legend()
plt.grid(True)
plt.show()

This code uses the Kalman filter to refine the trajectory prediction iteratively as more actual data points become available.

I obtained this plot:

Exobiology

This doesn't make sense in its current form. It's unable to model discontinuities on the ground. – Miticide

In the Kalman Filter output image above, the predicted trajectory deviates a lot from the actual trajectory especially at bouncing point of ball. Most likely due to linear nature of Kalman Filter. Maybe Extended Kalman Filter (EKF) or Unscented Kalman Filter (UKF) would work. – Vocative

Indeed, but EKF & UKF still perform poorly at bouncing points. I stumbled upon an interesting one to test: "Rao-Blackwellized Particle Filters". In a RBPF, the state space is divided into 2 parts: 1) Linear subspace: For parts of the state space that are linear, a Kalman filter is used; 2) Non-linear subspace: For parts that are non-linear, a particle filter is used. cf. arxiv.org/pdf/1301.3853 – Exobiology

Answer 3

You can calculate the discrete second derivative of Y to identify parabolic sections of motion.

from numpy import *
y=array([2.991964, 2.903274, 2.716584, 2.431894, 2.049204, 1.568514, 0.989824, 0.313134, 0.311512, 0.646741, 0.88397, 1.0232, 1.064429, 1.007658, 0.852887, 0.600116, 0.249345, 0.232557, 0.516523, 0.702488, 0.790454, 0.78042, 0.672385, 0.466351])
y_der2 = y[2:] - 2 * y[1:-1] + y[0:-2]

As you can see, second derivative is negative almost everywhere, except for 1-2 points in-between, where the ball bounces and experiences big positive acceleration. So each section where it is negative corresponds to free fall. Throw away one point at each side of such section for safety.

For free fall, Y is a quadratic function in time (or in X, which practically should be the same).

Y = -0.5 * g * t^2 + b * t + c

You can then apply polynomial regression to find the quadratic equation for Y.

Then, for each parabolic-motion section, find the theoretically predicted speed at bounce point. For each bounce point, the ratio between speeds in adjacent parabolic sections is the restitution coefficient. You can verify that it is approximately constant (maybe, for debugging, also verify another theoretically predicted equality: approximately equal X-points of bounce for adjacent parabolic sections).

This method fill fail when the ball bounces too fast, so that there are not enough measurements between the bounce points to apply polynomial regression. You should stop the calculations when such a condition appears.

P.S. I think your motion model should also have vx = e * bx when the ball bounces. Not sure how important it is for prediction accuracy. Anyway, the method I described doesn't depend on this detail.

Iridotomy

Answer 4

@anatolyg's method is the correct first step. After that,

• apply find_peaks;
• perform a first piecewise polynomial regression: first-degree in x and second-degree in y; then
• as a further step that I don't demonstrate, you need to enforce that the boundary positions match between each segment and then do an end-to-end fit where the physical parameters are shared across the whole dataset.

import matplotlib.pyplot as plt
import numpy as np
import scipy.signal


def fit(
    t: np.ndarray,
    x: np.ndarray,
    y: np.ndarray,
) -> tuple[
    list[np.polynomial.Polynomial],  # x(t)
    list[np.polynomial.Polynomial],  # y(t)
]:
    # Second-order differential. This assumes a monotonic t.
    d2ydt2 = np.gradient(y, 2)

    # Boundary conditions for each bounce segment
    bounce_idx, props = scipy.signal.find_peaks(d2ydt2)
    left_indices = (0, *bounce_idx)
    right_indices = (*bounce_idx, len(t))

    # Boolean arrays selecting each segment
    segment_predicates = [
        (d2ydt2 < 0)   # Must be falling
        & (t >= left)  # Must be within second-order peaks
        & (t < right)
        for left, right in zip(left_indices, right_indices)
    ]
    x_polys = [
        np.polynomial.polynomial.Polynomial.fit(
            x=t[predicate], y=x[predicate], symbol='t', deg=1,
        )
        for predicate in segment_predicates
    ]
    y_polys = [
        np.polynomial.polynomial.Polynomial.fit(
            x=t[predicate], y=y[predicate], symbol='t', deg=2,
        )
        for predicate in segment_predicates
    ]
    return x_polys, y_polys


def dump(
    x_polys: list[np.polynomial.Polynomial],
    y_polys: list[np.polynomial.Polynomial],
) -> None:
    for i, (xp, yp) in enumerate(zip(x_polys, y_polys)):
        print(f'Bounce {i}:')
        print(f'  x={xp}')
        print(f'  y={yp}')


def plot(
    t: np.ndarray,
    x: np.ndarray,
    y: np.ndarray,
    x_polys: list[np.polynomial.Polynomial],
    y_polys: list[np.polynomial.Polynomial],
) -> plt.Figure:
    fig, ax = plt.subplots()

    ax.scatter(x, y, marker='+', label='experiment')

    tfine = np.linspace(start=t[0], stop=t[-1], num=201)
    for xp, yp in zip(x_polys, y_polys):
        xt = xp(tfine)
        yt = yp(tfine)
        use = yt >= 0
        ax.plot(xt[use], yt[use])

    return fig


def main() -> None:
    x = np.array((
        7.410000e-03, 9.591000e-02, 2.844100e-01, 5.729100e-01, 9.614100e-01,
        1.449910e+00, 2.038410e+00, 2.726910e+00, 3.373700e+00, 4.040770e+00,
        4.800040e+00, 5.577610e+00, 6.355180e+00, 7.132750e+00, 7.910320e+00,
        8.687900e+00, 9.465470e+00, 1.020976e+01, 1.092333e+01, 1.163690e+01,
        1.235047e+01, 1.306404e+01, 1.377762e+01, 1.449119e+01,
    ))
    y = np.array((
        2.991964, 2.903274, 2.716584, 2.431894, 2.049204, 1.568514, 0.989824, 0.313134,
        0.311512, 0.646741, 0.88397 , 1.0232  , 1.064429, 1.007658, 0.852887, 0.600116,
        0.249345, 0.232557, 0.516523, 0.702488, 0.790454, 0.78042 , 0.672385, 0.466351,
    ))
    t = np.arange(len(x), dtype=x.dtype)
    x_polys, y_polys = fit(t=t, x=x, y=y)
    dump(x_polys=x_polys, y_polys=y_polys)
    plot(t=t, x=x, y=y, x_polys=x_polys, y_polys=y_polys)
    plt.show()


if __name__ == '__main__':
    main()

Bounce 0:
  x=1.01716 + 1.35975·(-1.0 + 0.28571429t)
  y=2.252799 - 1.339415·(-1.0 + 0.28571429t) - 0.60025·(-1.0 + 0.28571429t)²
Bounce 1:
  x=7.910324 + 1.555146·(-7.0 + 0.5t)
  y=0.852887 - 0.407542·(-7.0 + 0.5t) - 0.196·(-7.0 + 0.5t)²
Bounce 2:
  x=13.77761667 + 0.713575·(-22.0 + t)
  y=0.672385 - 0.1570345·(-22.0 + t) - 0.0489995·(-22.0 + t)²

Miticide

I have tried a few things. Would be great if you could look at EDIT_2 section of my updated question. – Vocative