Suppose that I have a sequence x(n) which is K * N long and that only the first N elements are different from zero. I'm assuming that N << K, say, for example, N = 10 and K = 100000. I want to calculate the FFT, by FFTW, of such a sequence. This is equivalent to having a sequence of length N and having a zero padding to K * N. Since N and K may be "large", I have a significant zero padding. I'm exploring if I can save some computation time avoid explicit zero padding.
The case K = 2
Let us begin by considering the case K = 2. In this case, the DFT of x(n) can be written as
If k is even, namely k = 2 * m, then
which means that such values of the DFT can be calculated through an FFT of a sequence of length N, and not K * N.
If k is odd, namely k = 2 * m + 1, then
which means that such values of the DFT can be again calculated through an FFT of a sequence of length N, and not K * N.
So, in conclusion, I can exchange a single FFT of length 2 * N with 2 FFTs of length N.
The case of arbitrary K
In this case, we have
On writing k = m * K + t, we have
So, in conclusion, I can exchange a single FFT of length K * N with K FFTs of length N. Since the FFTW has fftw_plan_many_dft, I can expect to have some gaining against the case of a single FFT.
To verify that, I have set up the following code
#include <stdio.h>
#include <stdlib.h> /* srand, rand */
#include <time.h> /* time */
#include <math.h>
#include <fstream>
#include <fftw3.h>
#include "TimingCPU.h"
#define PI_d 3.141592653589793
void main() {
const int N = 10;
const int K = 100000;
fftw_plan plan_zp;
fftw_complex *h_x = (fftw_complex *)malloc(N * sizeof(fftw_complex));
fftw_complex *h_xzp = (fftw_complex *)calloc(N * K, sizeof(fftw_complex));
fftw_complex *h_xpruning = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
fftw_complex *h_xhatpruning = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
fftw_complex *h_xhatpruning_temp = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
fftw_complex *h_xhat = (fftw_complex *)malloc(N * K * sizeof(fftw_complex));
// --- Random number generation of the data sequence
srand(time(NULL));
for (int k = 0; k < N; k++) {
h_x[k][0] = (double)rand() / (double)RAND_MAX;
h_x[k][1] = (double)rand() / (double)RAND_MAX;
}
memcpy(h_xzp, h_x, N * sizeof(fftw_complex));
plan_zp = fftw_plan_dft_1d(N * K, h_xzp, h_xhat, FFTW_FORWARD, FFTW_ESTIMATE);
fftw_plan plan_pruning = fftw_plan_many_dft(1, &N, K, h_xpruning, NULL, 1, N, h_xhatpruning_temp, NULL, 1, N, FFTW_FORWARD, FFTW_ESTIMATE);
TimingCPU timerCPU;
timerCPU.StartCounter();
fftw_execute(plan_zp);
printf("Stadard %f\n", timerCPU.GetCounter());
timerCPU.StartCounter();
double factor = -2. * PI_d / (K * N);
for (int k = 0; k < K; k++) {
double arg1 = factor * k;
for (int n = 0; n < N; n++) {
double arg = arg1 * n;
double cosarg = cos(arg);
double sinarg = sin(arg);
h_xpruning[k * N + n][0] = h_x[n][0] * cosarg - h_x[n][1] * sinarg;
h_xpruning[k * N + n][1] = h_x[n][0] * sinarg + h_x[n][1] * cosarg;
}
}
printf("Optimized first step %f\n", timerCPU.GetCounter());
timerCPU.StartCounter();
fftw_execute(plan_pruning);
printf("Optimized second step %f\n", timerCPU.GetCounter());
timerCPU.StartCounter();
for (int k = 0; k < K; k++) {
for (int p = 0; p < N; p++) {
h_xhatpruning[p * K + k][0] = h_xhatpruning_temp[p + k * N][0];
h_xhatpruning[p * K + k][1] = h_xhatpruning_temp[p + k * N][1];
}
}
printf("Optimized third step %f\n", timerCPU.GetCounter());
double rmserror = 0., norm = 0.;
for (int n = 0; n < N; n++) {
rmserror = rmserror + (h_xhatpruning[n][0] - h_xhat[n][0]) * (h_xhatpruning[n][0] - h_xhat[n][0]) + (h_xhatpruning[n][1] - h_xhat[n][1]) * (h_xhatpruning[n][1] - h_xhat[n][1]);
norm = norm + h_xhat[n][0] * h_xhat[n][0] + h_xhat[n][1] * h_xhat[n][1];
}
printf("rmserror %f\n", 100. * sqrt(rmserror / norm));
fftw_destroy_plan(plan_zp);
}
The approach I have developed consists of three steps:
- Multiplying the input sequence by "twiddle" complex exponentials;
- Performing the
fftw_many; - Reorganizing the results.
The fftw_many is faster than the single FFTW on K * N input points. However, steps #1 and #3 completely destroy such a gain. I would expect that steps #1 and #3 be computationally much lighter than step #2.
My questions are:
- How is it possible that steps #1 and #3 a so computationally more demanding than step #2?
- How can I improve steps #1 and #3 to have a net gain against the "standard" approach?
Thank you very much for any hint.
EDIT
I'm working with Visual Studio 2013 and compiling in Release mode.

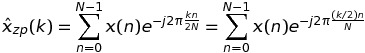
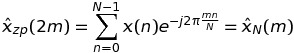
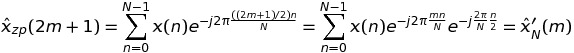
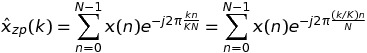
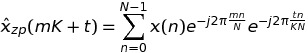
gcc -O3 ...? – Midlothian