How to create the most compact mapping n → isprime(n) up to a limit N?

Question

Naturally, for bool isprime(number) there would be a data structure I could query.
I define the best algorithm, to be the algorithm that produces a data structure with lowest memory consumption for the range (1, N], where N is a constant.
Just an example of what I am looking for: I could represent every odd number with one bit e.g. for the given range of numbers (1, 10], starts at 3: 1110

The following dictionary can be squeezed more, right? I could eliminate multiples of five with some work, but numbers that end with 1, 3, 7 or 9 must be there in the array of bits.

How do I solve the problem?

Humor

Your request is a little vague. You give a signature that tests a single number but then ask for a data structure of (1,N]. Do you want an algorithm that generates a dictionary<int,bool> or just a one-shot function that checks if a single number is prime? – Afterdamp

@Michael Sorry, that is the best description I could comeup with. What I am looking is excactly as you are saying: a boolean dictionary. I would like to minimize the space of the dictionary. Thanks :) – Humor

If that's what you're looking for it's been asked already: #1032927 – Kamila

You would need to Ask the NSA – Foppish

Note: for i in (2, a) runs the loop exactly twice: once with i == 2, and once with i == a. You probably wanted to use for i in range(2, a). – Urania

related: Miller–Rabin primality test in Python – Sacrosanct

(Characteristic function of primes: 1 if n is prime else 0) – Galvanoscope

Answer 1

The fastest algorithm for general prime testing is AKS. The Wikipedia article describes it at lengths and links to the original paper.

If you want to find big numbers, look into primes that have special forms like Mersenne primes.

The algorithm I usually implement (easy to understand and code) is as follows (in Python):

def isprime(n):
    """Returns True if n is prime."""
    if n == 2:
        return True
    if n == 3:
        return True
    if n % 2 == 0:
        return False
    if n % 3 == 0:
        return False

    i = 5
    w = 2

    while i * i <= n:
        if n % i == 0:
            return False

        i += w
        w = 6 - w

    return True

It's a variant of the classic O(sqrt(N)) algorithm. It uses the fact that a prime (except 2 and 3) is of form 6k - 1 or 6k + 1 and looks only at divisors of this form.

Sometimes, If I really want speed and the range is limited, I implement a pseudo-prime test based on Fermat's little theorem. If I really want more speed (i.e. avoid O(sqrt(N)) algorithm altogether), I precompute the false positives (see Carmichael numbers) and do a binary search. This is by far the fastest test I've ever implemented, the only drawback is that the range is limited.

Enjoyable

Strictly speaking Carmicheals are not sufficient. Your pseudo-prime test must also not inadvertently miss the right base required to disprove FLT. The strong pseudo-prime algorithm is superior in that there are no "Carmicheals" with respect to it, but you still cannot be sure unless you have checked at least one quarter of the range. If you are not range limited, then it would seem to me that using SPP + something like pollard rho to classify the vast majority of numbers of a first pass before using something more heavy duty is the right approach. – Hengel

@Paul Hsieh: modified the wording, do you find this better now? – Enjoyable

Two questions: Can you explain better what the variables i and w are, and what is meant by the form 6k-1 and 6k+1? Thank you for your insight and the code sample (which I'm trying to understand) – Chiastic

@Chiastic Here you go, quora.com/… – Inconsistent

Wouldn't it be better to calculate the sqrt of n once and comparing i to it, rather than calculating i * i every cycle of the loop? – Huffy

Actually AKS is NOT the fastest implementation. – Isoprene

@Isoprene ... but you can't fit the fastest implementation in the comment fields here to share with us? – Pravit

@GreenAsJade: Well the question as it is posed is ambigious when it comes to primality checks. The accepted answer holds this with saying that you have to decide between a probabilistic and deterministic approach, the former being a lot faster. – Isoprene

When it comes to deterministic tests, ECPP (most likely in the Goldwasser implementation) should be faster than AKS. – Isoprene

Check it with n = int(subprocess.check_output('openssl prime -generate -bits 2048 -hex'.split()), 16) :P – Sidky

Im no expert here, but I do believe if you check for divisibility by the base before running a Fermat prime probability test, you circumvent the trouble Carmichaels give you. Ex. 561 is Carmichael, but if you divide by 3 before testing a base 3 Fermat test, you find it divides perfectly and is clearly composite. I dont even understand why people stumble with Carmichaels on these tests. Testing for divisibility by each base I use is always my first step. Youre supposed to do this anyway since the base is supposed to be coprime. – Hattie

isprime(1) True - if n <= 3: return 2 <= n – Galvanoscope

Is this approximate, or can I rely on this to generate lists of primes in a given range? It's definitely waaay faster than everything I tried now. My initial (read: dumb) method took 1:17 to check that 100000007 is prime, my second method took half of that, 37 seconds, and this...took about 0.3 seconds! :O – Levis

Answer 2

A pretty simple and concise brute-force solution to check whether a number N is prime: simply check if there is any divisor of N from 2 up to the square root of N (see why here if interested).

The following code is compatible with both Python 2 and Python 3:

from math import sqrt
from itertools import count, islice

def is_prime(n):
    return n > 1 and all(n % i for i in islice(count(2), int(sqrt(n) - 1)))

And here's a simpler Python 3 only implementation:

def is_prime(n):
    return n > 1 and all(n % i for i in range(2, int(n ** 0.5) + 1))

Here are the extended versions of the above for clarity:

from math import sqrt
from itertools import count, islice

def is_prime(n):
    if n < 2:
        return False

    for divisor in islice(count(2), int(sqrt(n) - 1)):
        if n % divisor == 0:
            return False

    return True

def is_prime(n):
    if n < 2:
        return False

    for divisor in range(2, int(n ** 0.5) + 1):
        if n % divisor == 0:
            return False

    return True

This is not meant to be anything near the fastest nor the most optimal primality check algorithm, it only accomplishes the goal of being simple and concise, which also reduces implementation errors. It has a time complexity of O(sqrt(n)).

If you are looking for faster algorithms to check whether a number is prime, you might be interested in the following:

• Finding primes & proving primality: brief overview and explanation of the most famous primality tests and their history.
• Probabilistic primality tests (Wikipedia): these can be incorporated in the above code rather easily to skip the brute force if they do not pass, as an example there is this excellent answer to the duplicate of this question.
• Fast deterministic primaliry tests (Wikipedia)
• This Q&A Fastest way to list all primes below N along with the pyprimesieve library.

---

Implementation notes

You might have noticed that in the Python 2 compatible implementation I am using itertools.count() in combination with itertools.islice() instead of a simple range() or xrange() (the old Python 2 generator range, which in Python 3 is the default). This is because in CPython 2 xrange(N) for some N such that N > 2⁶³ ‒ 1 (or N > 2³¹ ‒ 1 depending on the implementation) raises an OverflowError. This is an unfortunate CPython implementation detail.

We can use itertools to overcome this issue. Since we are counting up from 2 to infinity using itertools.count(2), we'll reach sqrt(n) after sqrt(n) - 1 steps, and we can limit the generator using itertools.islice().

Organist

some cases would fail...I guess in for loop the end limit should be sqrt(n)+1 instead of sqrt(n)-1 – Will

@Will this has since been corrected (probably years ago, don't remember when). I've tested the code above and it correctly works for 1 <= N <= 1.000.000. – Organist

Answer 3

There are many efficient ways to test primality (and this isn't one of them), but the loop you wrote can be concisely rewritten in Python:

def is_prime(a):
    return all(a % i for i in xrange(2, a))

That is, a is prime if all numbers between 2 and a (not inclusive) give non-zero remainder when divided into a.

Caliph

note that is_prime returns True for 0 and 1. However, Wikipedia defines a prime number as "a natural number greater than 1 that has no positive divisors other than 1 and itself." so i changed it to return a > 1 and all(a % i for i in xrange(2, a)) – Darrickdarrill

DO NOT USE THIS FUNCTION! Here are the reasons. 1) Returns true if a == 1, but 1 is not considered a prime. 2) It checks if a number is prime until a - 1, but a decent programmer knows that it is necessary only up to sqrt(a). 3) It doesn't skip even numbers: except 2, all primes are odd numbers. 4) It doesn't show the algorithmic thinking behind how to find a prime number, because it uses Python's commodities. 5) xrange doesn't exist in Python 3, so some people will not be able to run it. – Discordance

Answer 4

This is the most efficient way to see if a number is prime, if you only have a few queries. If you ask a lot of numbers if they are prime, try Sieve of Eratosthenes.

import math

def is_prime(n):
    if n == 2:
        return True
    if n % 2 == 0 or n <= 1:
        return False

    sqr = int(math.sqrt(n)) + 1

    for divisor in range(3, sqr, 2):
        if n % divisor == 0:
            return False
    return True

Bridgehead

You can also do this without importing math with the following sqr = int(n ** 0.5) + 1 – Montagu

Answer 5

If a is a prime then the while x: in your code will run forever, since x will remain True.

So why is that while there?

I think you wanted to end the for loop when you found a factor, but didn't know how, so you added that while since it has a condition. So here is how you do it:

def is_prime(a):
    x = True 
    for i in range(2, a):
       if a%i == 0:
           x = False
           break # ends the for loop
       # no else block because it does nothing ...


    if x:
        print "prime"
    else:
        print "not prime"

Authoritative

Answer 6

I compared the efficiency of the most popular suggestions to determine if a number is prime. I used python 3.6 on ubuntu 17.10; I tested with numbers up to 100.000 (you can test with bigger numbers using my code below).

This first plot compares the functions (which are explained further down in my answer), showing that the last functions do not grow as fast as the first one when increasing the numbers.

And in the second plot we can see that in case of prime numbers the time grows steadily, but non-prime numbers do not grow so fast in time (because most of them can be eliminated early on).

Here are the functions I used:

1. this answer and this answer suggested a construct using all():

   def is_prime_1(n):
       return n > 1 and all(n % i for i in range(2, int(math.sqrt(n)) + 1))
   

2. This answer used some kind of while loop:

   def is_prime_2(n):
       if n <= 1:
           return False
       if n == 2:
           return True
       if n == 3:
           return True
       if n % 2 == 0:
           return False
       if n % 3 == 0:
           return False
   
       i = 5
       w = 2
       while i * i <= n:
           if n % i == 0:
               return False
           i += w
           w = 6 - w
   
       return True
   

3. This answer included a version with a for loop:

   def is_prime_3(n):
       if n <= 1:
           return False
   
       if n % 2 == 0 and n > 2:
           return False
   
       for i in range(3, int(math.sqrt(n)) + 1, 2):
           if n % i == 0:
               return False
   
       return True
   

4. And I mixed a few ideas from the other answers into a new one:

   def is_prime_4(n):
       if n <= 1:          # negative numbers, 0 or 1
           return False
       if n <= 3:          # 2 and 3
           return True
       if n % 2 == 0 or n % 3 == 0:
           return False
   
       for i in range(5, int(math.sqrt(n)) + 1, 2):
           if n % i == 0:
               return False
   
       return True
   

---

Here is my script to compare the variants:

import math
import pandas as pd
import seaborn as sns
import time
from matplotlib import pyplot as plt


def is_prime_1(n):
    ...
def is_prime_2(n):
    ...
def is_prime_3(n):
    ...
def is_prime_4(n):
    ...

default_func_list = (is_prime_1, is_prime_2, is_prime_3, is_prime_4)

def assert_equal_results(func_list=default_func_list, n):
    for i in range(-2, n):
        r_list = [f(i) for f in func_list]
        if not all(r == r_list[0] for r in r_list):
            print(i, r_list)
            raise ValueError
    print('all functions return the same results for integers up to {}'.format(n))

def compare_functions(func_list=default_func_list, n):
    result_list = []
    n_measurements = 3

    for f in func_list:
        for i in range(1, n + 1):
            ret_list = []
            t_sum = 0
            for _ in range(n_measurements):
                t_start = time.perf_counter()
                is_prime = f(i)
                t_end = time.perf_counter()

                ret_list.append(is_prime)
                t_sum += (t_end - t_start)

            is_prime = ret_list[0]
            assert all(ret == is_prime for ret in ret_list)
            result_list.append((f.__name__, i, is_prime, t_sum / n_measurements))

    df = pd.DataFrame(
        data=result_list,
        columns=['f', 'number', 'is_prime', 't_seconds'])
    df['t_micro_seconds'] = df['t_seconds'].map(lambda x: round(x * 10**6, 2))
    print('df.shape:', df.shape)

    print()
    print('', '-' * 41)
    print('| {:11s} | {:11s} | {:11s} |'.format(
        'is_prime', 'count', 'percent'))
    df_sub1 = df[df['f'] == 'is_prime_1']
    print('| {:11s} | {:11,d} | {:9.1f} % |'.format(
        'all', df_sub1.shape[0], 100))
    for (is_prime, count) in df_sub1['is_prime'].value_counts().iteritems():
        print('| {:11s} | {:11,d} | {:9.1f} % |'.format(
            str(is_prime), count, count * 100 / df_sub1.shape[0]))
    print('', '-' * 41)

    print()
    print('', '-' * 69)
    print('| {:11s} | {:11s} | {:11s} | {:11s} | {:11s} |'.format(
        'f', 'is_prime', 't min (us)', 't mean (us)', 't max (us)'))
    for f, df_sub1 in df.groupby(['f', ]):
        col = df_sub1['t_micro_seconds']
        print('|{0}|{0}|{0}|{0}|{0}|'.format('-' * 13))
        print('| {:11s} | {:11s} | {:11.2f} | {:11.2f} | {:11.2f} |'.format(
            f, 'all', col.min(), col.mean(), col.max()))
        for is_prime, df_sub2 in df_sub1.groupby(['is_prime', ]):
            col = df_sub2['t_micro_seconds']
            print('| {:11s} | {:11s} | {:11.2f} | {:11.2f} | {:11.2f} |'.format(
                f, str(is_prime), col.min(), col.mean(), col.max()))
    print('', '-' * 69)

    return df

Running the function compare_functions(n=10**5) (numbers up to 100.000) I get this output:

df.shape: (400000, 5)

 -----------------------------------------
| is_prime    | count       | percent     |
| all         |     100,000 |     100.0 % |
| False       |      90,408 |      90.4 % |
| True        |       9,592 |       9.6 % |
 -----------------------------------------

 ---------------------------------------------------------------------
| f           | is_prime    | t min (us)  | t mean (us) | t max (us)  |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_1  | all         |        0.57 |        2.50 |      154.35 |
| is_prime_1  | False       |        0.57 |        1.52 |      154.35 |
| is_prime_1  | True        |        0.89 |       11.66 |       55.54 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_2  | all         |        0.24 |        1.14 |      304.82 |
| is_prime_2  | False       |        0.24 |        0.56 |      304.82 |
| is_prime_2  | True        |        0.25 |        6.67 |       48.49 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_3  | all         |        0.20 |        0.95 |       50.99 |
| is_prime_3  | False       |        0.20 |        0.60 |       40.62 |
| is_prime_3  | True        |        0.58 |        4.22 |       50.99 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_4  | all         |        0.20 |        0.89 |       20.09 |
| is_prime_4  | False       |        0.21 |        0.53 |       14.63 |
| is_prime_4  | True        |        0.20 |        4.27 |       20.09 |
 ---------------------------------------------------------------------

Then, running the function compare_functions(n=10**6) (numbers up to 1.000.000) I get this output:

df.shape: (4000000, 5)

 -----------------------------------------
| is_prime    | count       | percent     |
| all         |   1,000,000 |     100.0 % |
| False       |     921,502 |      92.2 % |
| True        |      78,498 |       7.8 % |
 -----------------------------------------

 ---------------------------------------------------------------------
| f           | is_prime    | t min (us)  | t mean (us) | t max (us)  |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_1  | all         |        0.51 |        5.39 |     1414.87 |
| is_prime_1  | False       |        0.51 |        2.19 |      413.42 |
| is_prime_1  | True        |        0.87 |       42.98 |     1414.87 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_2  | all         |        0.24 |        2.65 |      612.69 |
| is_prime_2  | False       |        0.24 |        0.89 |      322.81 |
| is_prime_2  | True        |        0.24 |       23.27 |      612.69 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_3  | all         |        0.20 |        1.93 |       67.40 |
| is_prime_3  | False       |        0.20 |        0.82 |       61.39 |
| is_prime_3  | True        |        0.59 |       14.97 |       67.40 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_4  | all         |        0.18 |        1.88 |      332.13 |
| is_prime_4  | False       |        0.20 |        0.74 |      311.94 |
| is_prime_4  | True        |        0.18 |       15.23 |      332.13 |
 ---------------------------------------------------------------------

---

I used the following script to plot the results:

def plot_1(func_list=default_func_list, n):
    df_orig = compare_functions(func_list=func_list, n=n)
    df_filtered = df_orig[df_orig['t_micro_seconds'] <= 20]
    sns.lmplot(
        data=df_filtered, x='number', y='t_micro_seconds',
        col='f',
        # row='is_prime',
        markers='.',
        ci=None)

    plt.ticklabel_format(style='sci', axis='x', scilimits=(3, 3))
    plt.show()

Submarginal

Answer 7

One can use sympy.

import sympy

sympy.ntheory.primetest.isprime(33393939393929292929292911111111)

True

From sympy docs. The first step is looking for trivial factors, which if found enables a quick return. Next, if the sieve is large enough, use bisection search on the sieve. For small numbers, a set of deterministic Miller-Rabin tests are performed with bases that are known to have no counterexamples in their range. Finally if the number is larger than 2^64, a strong BPSW test is performed. While this is a probable prime test and we believe counterexamples exist, there are no known counterexamples

Geomancy

Answer 8

According to wikipedia, the Sieve of Eratosthenes has complexity O(n * (log n) * (log log n)) and requires O(n) memory - so it's a pretty good place to start if you aren't testing for especially large numbers.

Starlike

Sorry I know my description is vague, I am not looking at SOE :) look at my comment @Michael – Humor

@AraK: You say you want a data structure to hold the primality status of all n up to a limit though. While dedicated primality testing functions are going to be faster for any given n, if you want to know all the results from 2 to n, with minimal cost, a Sieve of Eratosthenes with optimized storage (e.g. using a byte to represent the primality status of all numbers in a block of 30, after removing all numbers divisible by 2, 3 and 5, and hard-coding primes below 30) is how you'd populate it. Only practical to populate to a limit (e.g. w/4 GB RAM, you could store up to ~129 billion). – Inimical

Answer 9

bool isPrime(int n)
{
    // Corner cases
    if (n <= 1)  return false;
    if (n <= 3)  return true;
 
    // This is checked so that we can skip 
    // middle five numbers in below loop
    if (n%2 == 0 || n%3 == 0) return false;
 
    for (int i=5; i*i<=n; i=i+6)
        if (n%i == 0 || n%(i+2) == 0)
           return false;
 
    return true;
}

This is just c++ implementation of above

Nickels

Its one of the most efficient deterministic algorithms Ive come across, yes, but its not an implementation of AKS. The AKS system is much newer than the algorithm outlined. It is arguably more efficient, but is somewhat difficult to implement, imo, on account of potentially astronomically large factorials / binomial coefficients. – Hattie

How is this different from Derri Leahi's (non-)answer (other than C instead of Java)? How does this answer What is the algorithm that produces a data structure with lowest memory consumption for the range (1, N]? – Galvanoscope

How does (n%i == 0 || n%(i+2) == 0) correspond to 6n+1 & 6n-1? – Swagsman

@YeshwanthVenkatesh: How does (n%i == 0 || n%(i+2) == 0) correspond to 6n+1 & 6n-1? part of the answer is different roles for n, the other is 6n+1 & 6n-1 equivalent to (6n-1)+0 & (6n-1)+2*. – Galvanoscope

Also note that this algorithm doesn't give the correct result for 5 and 7. – Deputize

You may also be better off checking if the number is 6n+/-1 before the loop. If not, it's guaranteed to be non-prime, making the loop unnecessary. – Deception

@Deception that's what if (n%2 == 0 || n%3 == 0) return false; is already doing. – Madalynmadam

Answer 10

For large numbers you cannot simply naively check whether the candidate number N is divisible by none of the numbers less than sqrt(N). There are much more scalable tests available, such as the Miller-Rabin primality test. Below you have implementation in python:

def is_prime(x):
    """Fast implementation fo Miller-Rabin primality test, guaranteed to be correct."""
    import math
    def get_sd(x):
        """Returns (s: int, d: int) for which x = d*2^s """
        if not x: return 0, 0
        s = 0
        while 1:
            if x % 2 == 0:
                x /= 2
                s += 1
            else:
                return s, x
    if x <= 2:
        return x == 2
    # x - 1 = d*2^s
    s, d = get_sd(x - 1)
    if not s:
        return False  # divisible by 2!
    log2x = int(math.log(x) / math.log(2)) + 1
    # As long as Riemann hypothesis holds true, it is impossible
    # that all the numbers below this threshold are strong liars.
    # Hence the number is guaranteed to be a prime if no contradiction is found.
    threshold = min(x, 2*log2x*log2x+1)
    for a in range(2, threshold):
        # From Fermat's little theorem if x is a prime then a^(x-1) % x == 1
        # Hence the below must hold true if x is indeed a prime:
        if pow(a, d, x) != 1:
            for r in range(0, s):
                if -pow(a, d*2**r, x) % x == 1:
                    break
            else:
                # Contradicts Fermat's little theorem, hence not a prime.
                return False
    # No contradiction found, hence x must be a prime.
    return True

You can use it to find huge prime numbers:

x = 10000000000000000000000000000000000000000000000000000000000000000000000000000
for e in range(1000):
    if is_prime(x + e):
        print('%d is a prime!' % (x + e))
        break

# 10000000000000000000000000000000000000000000000000000000000000000000000000133 is a prime!

If you are testing random integers probably you want to first test whether the candidate number is divisible by any of the primes smaller than, say 1000, before you call Miller-Rabin. This will help you filter out obvious non-primes such as 10444344345.

Daredevil

This is the Miller test. The Miller-Rabin test is the probabilistic version where randomly selected bases are tested until sufficient confidence is achieved. Also, the Miller test is not dependent on the Riemann Hypothesis directly, but the Generalized Riemann Hypothesis (GRH) for quadratic Diriclet characters (I know it's a mouthful, and I don't understand it either). Which means a potential proof for the Riemann Hypothesis may not even apply to the GRH, and hence not prove the Miller test correct. Even worse case would be of course if the GRH is disproved. – Chuckle

is_prime(7699) -> TypeError: pow() 3rd argument not allowed unless all arguments are integers – Valentinvalentina

Can I used your code in one of my libraries? How many number of itertions does the above give? – Pretorius

Answer 11

Python 3:

def is_prime(a):
    return a > 1 and all(a % i for i in range(2, int(a**0.5) + 1))

Stony

Answer 12

Way too late to the party, but hope this helps. This is relevant if you are looking for big primes:

To test large odd numbers you need to use the Fermat-test and/or Miller-Rabin test.

These tests use modular exponentiation which is quite expensive, for n bits exponentiation you need at least n big int multiplication and n big int divison. Which means the complexity of modular exponentiation is O(n³).

So before using the big guns, you need to do quite a few trial divisions. But don't do it naively, there is a way to do them fast. First multiply as many primes together as many fits into a the words you use for the big integers. If you use 32 bit words, multiply 3*5*7*11*13*17*19*23*29=3234846615 and compute the greatest common divisor with the number you test using the Euclidean algorithm. After the first step the number is reduced below the word size and continue the algorithm without performing complete big integer divisions. If the GCD != 1, that means one of the primes you multiplied together divides the number, so you have a proof it's not prime. Then continue with 31*37*41*43*47 = 95041567, and so on.

Once you tested several hundred (or thousand) primes this way, you can do 40 rounds of Miller-Rabin test to confirm the number is prime, after 40 rounds you can be certain the number is prime there is only 2^-80 chance it's not (it's more likely your hardware malfunctions...).

Idiographic

Answer 13

I have got a prime function which works until (2^61)-1 Here:

from math import sqrt
def isprime(num): num > 1 and return all(num % x for x in range(2, int(sqrt(num)+1)))

Explanation:

The all() function can be redefined to this:

def all(variables):
    for element in variables:
        if not element: return False
    return True

The all() function just goes through a series of bools / numbers and returns False if it sees 0 or False.

The sqrt() function is just doing the square root of a number.

For example:

>>> from math import sqrt
>>> sqrt(9)
>>> 3
>>> sqrt(100)
>>> 10

The num % x part returns the remainder of num / x.

Finally, range(2, int(sqrt(num))) means that it will create a list that starts at 2 and ends at int(sqrt(num)+1)

For more information about range, have a look at this website!

The num > 1 part is just checking if the variable num is larger than 1, becuase 1 and 0 are not considered prime numbers.

I hope this helped :)

Wedged

Please argue how this is the best algorithm, or even a good one. – Galvanoscope

@Galvanoscope , Most prime functions here dont go up to (2^31)-1 or takes too long for high numbers, but mine works until (2^61)-1, so you can check if a number is prime with a wider range of numbers. – Wedged

Answer 14

In Python:

def is_prime(n):
    return not any(n % p == 0 for p in range(2, int(math.sqrt(n)) + 1))

A more direct conversion from mathematical formalism to Python would use all(n % p != 0... ), but that requires strict evaluation of all values of p. The not any version can terminate early if a True value is found.

Chamberlin

Wrt "all(n % p != 0... ), but that requires strict evaluation of all values of p" - that's incorrect. any and all will both exit early. So at the first p where n % p is 0, all would exit. – Fadge

Answer 15

best algorithm for Primes number javascript

 function isPrime(num) {
      if (num <= 1) return false;
      else if (num <= 3) return true;
      else if (num % 2 == 0 || num % 3 == 0) return false;
      var i = 5;
      while (i * i <= num) {
        if (num % i == 0 || num % (i + 2) == 0) return false;
        i += 6;
      }
      return true
    }

Elbe

Answer 16

A prime number is any number that is only divisible by 1 and itself. All other numbers are called composite.

The simplest way, of finding a prime number, is to check if the input number is a composite number:

    function isPrime(number) {
        // Check if a number is composite
        for (let i = 2; i < number; i++) {
            if (number % i === 0) {
                return false;
            }
        }
        // Return true for prime numbers
        return true;
    }

The program has to divide the value of number by all the whole numbers from 1 and up to the its value. If this number can be divided evenly not only by one and itself it is a composite number.

The initial value of the variable i has to be 2 because both prime and composite numbers can be evenly divided by 1.

    for (let i = 2; i < number; i++)

Then i is less than number for the same reason. Both prime and composite numbers can be evenly divided by themselves. Therefore there is no reason to check it.

Then we check whether the variable can be divided evenly by using the remainder operator.

    if (number % i === 0) {
        return false;
    }

If the remainder is zero it means that number can be divided evenly, hence being a composite number and returning false.

If the entered number didn't meet the condition, it means it's a prime number and the function returns true.

Richart

(While I think simplest one valid interpretation of best:) The question is What is the best algorithm for checking if a number is prime?: Is checking for divisibility where number / 2 < i < number advantageous? What about number < i*i? What do the understandable ones of the other 3³ answers say? – Galvanoscope

Just to be clear, 1 is neither prime nor composite. And primes are drawn from positive integers. – Deception

Answer 17

BEST SOLUTION

I an unsure if I understand the concept of Time complexity: O(sqrt(n)) and Space complexity: O(1) in this context but the function prime(n) is probably the fastest way (least iterations) to calculate if a number is prime number of any size.

https://github.com/ganeshkbhat/fastprimenumbers

This probably is the BEST solution in the internet as of today 11th March 2022. Feedback and usage is welcome.

This same code can be applied in any languages like C, C++, Go Lang, Java, .NET, Python, Rust, etc with the same logic and have performance benefits. It is pretty fast. I have not seen this implemented before and has been indigenously done.

If you are looking at the speed and performance here is the """BEST""" hopeful solution I can give:

Max iterations 16666 for n == 100000 instead of 100000 of conventional way

The codes can also be found here: https://github.com/ganeshkbhat/fastprimecalculations

If you use it for your project please spend 2 minutes of your time crediting me by letting me know by either sending me an email, or logging an Github issue with subject heading [User], or star my Github project. But let me know here https://github.com/ganeshkbhat/fastprimecalculations. I would love to know the fans and users of the code logic

def prime(n):
    if ((n == 2 or n == 3 or n == 5 or n == 7)):
        return True
    
    if (n == 1 or ((n > 7) and (n % 5 == 0 or n % 7 == 0 or n % 2 == 0 or n % 3 == 0))):
        return False
    
    if ( type((n - 1) / 6) == int or type((n + 1) / 6) == int):
        for i in range(1, n):
            factorsix = (i * 6)
            five = n / (5 + factorsix)
            seven = n / (7 + factorsix)
            if ( ((five > 1) and type(five) == int) or ((seven > 1) and type(five) == int) ):
                return False;
            
            if (factorsix > n):
                break;
        return True
    return False

Here is an analysis of all the ways of calculation:

Conventional way of checking for prime:

def isPrimeConventionalWay(n):
    count = 0
    if (n <= 1):
        return False;
    # Check from 2 to n-1
    # Max iterations 99998 for n == 100000 
    for i in range(2,n):
        # Counting Iterations
        count += 1
        if (n % i == 0):
            print("count: Prime Conventional way", count)
            return False;
    print("count: Prime Conventional way", count)
    return True;

SQUAREROOT way of checking for prime:

def isPrimeSquarerootWay(num):
    count = 0
    # if not is_number num return False
    if (num < 2):
        print("count: Prime Squareroot way", count)
        return False
    
    s = math.sqrt(num)
    for  i in range(2, num):
        # Counting Iterations
        count += 1
        if (num % i == 0):
            print("count: Prime Squareroot way", count)
            return False
    print("count: Prime Squareroot way", count)
    return True

OTHER WAYS:

def isprimeAKSWay(n):
    """Returns True if n is prime."""
    count = 0
    if n == 2:
        return True
    if n == 3:
        return True
    if n % 2 == 0:
        return False
    if n % 3 == 0:
        return False

    i = 5
    w = 2

    while i * i <= n:
        count += 1
        if n % i == 0:
            print("count: Prime AKS - Mersenne primes - Fermat's little theorem or whatever way", count)
            return False

        i += w
        w = 6 - w
    print("count: Prime AKS - Mersenne primes - Fermat's little theorem or whatever way", count)
    return True

SUGGESTED way of checking for prime:

def prime(n):
    count = 0
    if ((n == 2 or n == 3 or n == 5 or n == 7)):
        print("count: Prime Unconventional way", count)
        return True
    
    if (n == 1 or ((n > 7) and (n % 5 == 0 or n % 7 == 0 or n % 2 == 0 or n % 3 == 0))):
        print("count: Prime Unconventional way", count)
        return False
    
    if (((n - 1) / 6).is_integer()) or (((n + 1) / 6).is_integer()):
        for i in range(1, n):
            # Counting Iterations
            count += 1
            five = 5 + (i * 6)
            seven = 7 + (i * 6)
            if ((((n / five) > 1) and (n / five).is_integer()) or (((n / seven) > 1) and ((n / seven).is_integer()))):
                print("count: Prime Unconventional way", count)
                return False;
            
            if ((i * 6) > n):
                # Max iterations 16666 for n == 100000 instead of 100000
                break;
            
        print("count: Prime Unconventional way", count)
        return True
    
    print("count: Prime Unconventional way", count)
    return False

Tests to compare with the traditional way of checking for prime numbers.

def test_primecalculations():
    count = 0
    iterations = 100000
    arr = []
    for i in range(1, iterations):
        traditional = isPrimeConventionalWay(i)
        newer = prime(i)
        if (traditional == newer):
            count = count + 1
        else:
            arr.push([traditional, newer, i])
    print("[count, iterations, arr] list: ", count, iterations, arr)
    if (count == iterations):
        return True
    return False


# print("Tests Passed: ", test_primecalculations())
    

You will see the results of count of number of iterations as below for check of prime number: 100007:

print("Is Prime 100007: ", isPrimeConventionalWay(100007))
print("Is Prime 100007: ", isPrimeSquarerootWay(100007))
print("Is Prime 100007: ", prime(100007))
print("Is Prime 100007: ", isprimeAKSWay(100007))

count: Prime Conventional way 96
Is Prime 100007:  False
count: Prime Squareroot way 96
Is Prime 100007:  False
count: Prime Unconventional way 15
Is Prime 100007:  False
count: Prime AKS - Mersenne primes - Fermat's little theorem or whatever way 32
Is Prime 100007:  False

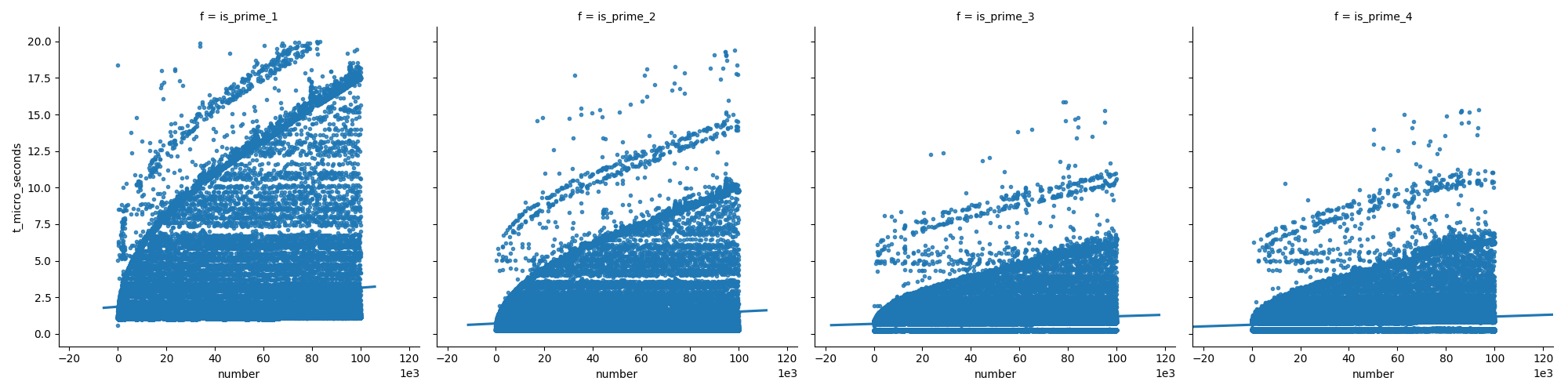
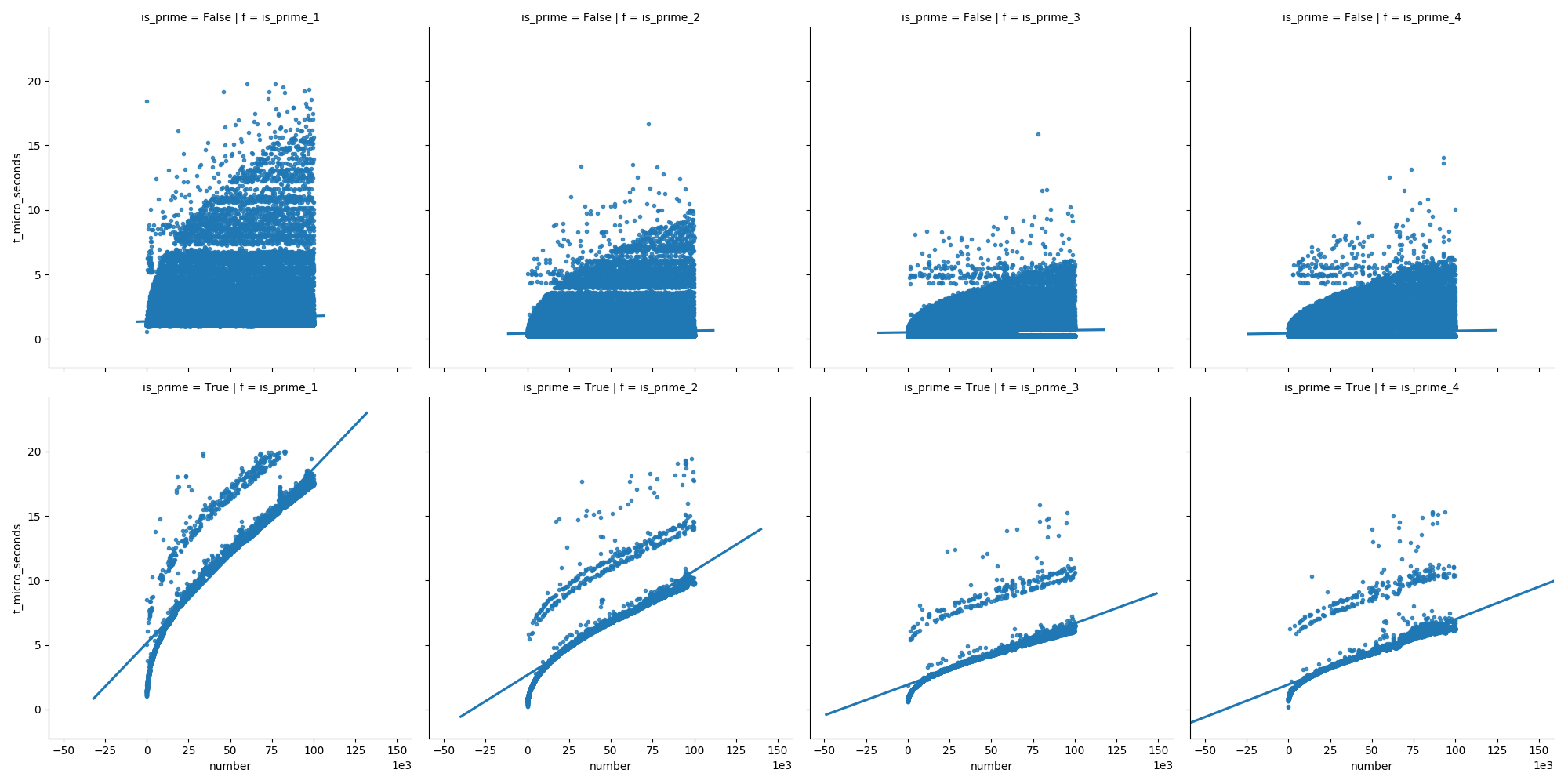
Here are some performance tests and results below:

import time
isPrimeConventionalWayArr = []
isPrimeSquarerootWayArr = []
primeArr = []
isprimeAKSWayArr = []


def tests_performance_isPrimeConventionalWayArr():
    global isPrimeConventionalWayArr
    for i in range(1, 1000000):
        start = time.perf_counter_ns()
        isPrimeConventionalWay(30000239)
        end = time.perf_counter_ns()
        isPrimeConventionalWayArr.append(end - start)
tests_performance_isPrimeConventionalWayArr()


def tests_performance_isPrimeSquarerootWayArr():
    global isPrimeSquarerootWayArr
    for i in range(1, 1000000):
        start = time.perf_counter_ns()
        isPrimeSquarerootWay(30000239)
        end = time.perf_counter_ns()
        isPrimeSquarerootWayArr.append(end - start)
tests_performance_isPrimeSquarerootWayArr()


def tests_performance_primeArr():
    global primeArr
    for i in range(1, 1000000):
        start = time.perf_counter_ns()
        prime(30000239)
        end = time.perf_counter_ns()
        primeArr.append(end - start)
tests_performance_primeArr()

def tests_performance_isprimeAKSWayArr():
    global isprimeAKSWayArr
    for i in range(1, 1000000):
        start = time.perf_counter_ns()
        isprimeAKSWay(30000239)
        end = time.perf_counter_ns()
        isprimeAKSWayArr.append(end - start)
tests_performance_isprimeAKSWayArr()  


print("isPrimeConventionalWayArr: ", sum(isPrimeConventionalWayArr)/len(isPrimeConventionalWayArr))
print("isPrimeSquarerootWayArr: ", sum(isPrimeSquarerootWayArr)/len(isPrimeSquarerootWayArr))
print("primeArr: ", sum(primeArr)/len(primeArr))
print("isprimeAKSWayArr: ", sum(isprimeAKSWayArr)/len(isprimeAKSWayArr))

Sample 1 Million Iterations

Iteration 1:

isPrimeConventionalWayArr:  1749.97224997225
isPrimeSquarerootWayArr:  1835.6258356258356
primeArr (suggested):  475.2365752365752
isprimeAKSWayArr:  1177.982377982378

Iteration 2:

isPrimeConventionalWayArr:  1803.141403141403
isPrimeSquarerootWayArr:  2184.222484222484
primeArr (suggested):  572.6434726434726
isprimeAKSWayArr:  1403.3838033838033

Iteration 3:

isPrimeConventionalWayArr:  1876.941976941977
isPrimeSquarerootWayArr:  2190.43299043299
primeArr (suggested):  569.7365697365698
isprimeAKSWayArr:  1449.4147494147494

Iteration 4:

isPrimeConventionalWayArr:  1873.2779732779734
isPrimeSquarerootWayArr:  2177.154777154777
primeArr (suggested):  590.4243904243905
isprimeAKSWayArr:  1401.9143019143019

Iteration 5:

isPrimeConventionalWayArr:  1891.1986911986912
isPrimeSquarerootWayArr:  2218.093218093218
primeArr (suggested):  571.6938716938716
isprimeAKSWayArr:  1397.6471976471976

Iteration 6:

isPrimeConventionalWayArr:  1868.8454688454688
isPrimeSquarerootWayArr:  2168.034368034368
primeArr (suggested):  566.3278663278663
isprimeAKSWayArr:  1393.090193090193

Iteration 7:

isPrimeConventionalWayArr:  1879.4764794764794
isPrimeSquarerootWayArr:  2199.030199030199
primeArr (suggested):  574.055874055874
isprimeAKSWayArr:  1397.7587977587978

Iteration 8:

isPrimeConventionalWayArr:  1789.2868892868894
isPrimeSquarerootWayArr:  2182.3258823258825
primeArr (suggested):  569.3206693206694
isprimeAKSWayArr:  1407.1486071486072

Pretorius

I don't see compact or memory requirements mentioned: How does this answer What is the algorithm that produces a data structure with lowest memory consumption for the range (1, N]? I don't see a programming language stated for the code presented: Is that Python 2? – Galvanoscope

@Galvanoscope seemingly it even breaks a thesis Pierre de Fermat - If N is a prime number, then bN – b is always a multiple of N, no matter what b is which in mathematical caculations have a very high space complexity as N increases. in very rare cases, N can satisfy this condition and still be composite. some fermat text is here quantamagazine.org/… – Pretorius

or the super computer in your browser way ;-) npmjs.com/package/@stdlib/dist-datasets-primes-100k – Pretorius

sqroot way at the moment is what gives the least iterations (reason for - or whatever way) . no intent or dropping names here. Conventional iteration way for 300530164787 is 1180 looks conspicuously low - because it is not prime – Pretorius

well what are your views on the SUGGESTED way of checking for prime: way for a performance check and publication against fermat and sqroot and aks way based on the above comments. i called it fast prime - npmjs.com/package/fast-prime pypi.org/project/fast-prime – Pretorius

Answer 18

Smallest memory? This isn't smallest, but is a step in the right direction.

class PrimeDictionary {
    BitArray bits;

    public PrimeDictionary(int n) {
        bits = new BitArray(n + 1);
        for (int i = 0; 2 * i + 3 <= n; i++) {
            bits.Set(i, CheckPrimality(2 * i + 3));
        }
    }

    public PrimeDictionary(IEnumerable<int> primes) {
        bits = new BitArray(primes.Max());
        foreach(var prime in primes.Where(p => p != 2)) {
            bits.Set((prime - 3) / 2, true);
        }
    }

    public bool IsPrime(int k) {
        if (k == 2) {
            return true;
        }
        if (k % 2 == 0) {
            return false;
        }
        return bits[(k - 3) / 2];
    }
}

Of course, you have to specify the definition of CheckPrimality.

Zed

Answer 19

Similar idea to the algorithm which has been mentioned

public static boolean isPrime(int n) {
    
    if(n == 2 || n == 3) return true;
    if((n & 1 ) == 0 || n % 3 == 0) return false;
    int limit = (int)Math.sqrt(n) + 1;
    for(int i = 5, w = 2; i <= limit; i += w, w = 6 - w) {
        if(n % i == 0) return false;
        numChecks++;
    }
    return true;
}

Whiffen

No relation to AKS algorithm. – Galvanoscope

In the for loop you do not need to check "i <= limit" , it is enough to ckeck "i < limit". So in every iteration you make one comparison less. – Savadove

Answer 20

To find if the number or numbers in a range is/are prime.

#!usr/bin/python3

def prime_check(*args):
    for arg in args:
        if arg > 1:     # prime numbers are greater than 1
            for i in range(2,arg):   # check for factors
                if(arg % i) == 0:
                    print(arg,"is not Prime")
                    print(i,"times",arg//i,"is",arg)
                    break
            else:
                print(arg,"is Prime")
                
            # if input number is less than
            # or equal to 1, it is not prime
        else:
            print(arg,"is not Prime")
    return
    
# Calling Now
prime_check(*list(range(101)))  # This will check all the numbers in range 0 to 100 
prime_check(#anynumber)         # Put any number while calling it will check.

Gestate

Run this code it will work for both a list and a particular number – Gestate

Answer 21

myInp=int(input("Enter a number: "))
if myInp==1:
    print("The number {} is neither a prime not composite no".format(myInp))
elif myInp>1:
    for i in range(2,myInp//2+1):
        if myInp%i==0:
            print("The Number {} is not a prime no".format(myInp))
            print("Because",i,"times",myInp//i,"is",myInp)
            break
    else:
        print("The Number {} is a prime no".format(myInp))
else:
    print("Alas the no {} is a not a prime no".format(myInp))

Bromate

When you write an answer, even if it's correct, please also write a bit explaining what you are doing, and why. This way people reading your answer can grasp easier what you have solved. Thank you! – Karli

Sure Kim ,thank you for pointing that out .This is my first program in Stackoverflow henceforth i will add appropriate comments and explanation . – Bromate

Answer 22

public static boolean isPrime(int number) {
 if(number < 2)
   return false;
 else if(number == 2 || number == 3)
        return true;
      else {
        for(int i=2;i<=number/2;i++)
           if(number%i == 0)
             return false;
           else if(i==number/2)
                return true;
      }
    return false;
}

Nonferrous

Answer 23

Most of previous answers are correct but here is one more way to test to see a number is prime number. As refresher, prime numbers are whole number greater than 1 whose only factors are 1 and itself.(source)

Solution:

Typically you can build a loop and start testing your number to see if it's divisible by 1,2,3 ...up to the number you are testing ...etc but to reduce the time to check, you can divide your number by half of the value of your number because a number cannot be exactly divisible by anything above half of it's value. Example if you want to see 100 is a prime number you can loop through up to 50.

Actual code:

def find_prime(number):
    if(number ==1):
        return False
    # we are dividiing and rounding and then adding the remainder to increment !
    # to cover not fully divisible value to go up forexample 23 becomes 11
    stop=number//2+number%2
    #loop through up to the half of the values
    for item in range(2,stop):
        if number%item==0:
           return False
        print(number)
    return True


if(find_prime(3)):
    print("it's a prime number !!")
else:
    print("it's not a prime")  

Greenaway

You only need to check to the square root of the number, which is quite a bit smaller than half the number. E.g. for n=100 you only need to check to 10, not 50. Why? At exactly the square root, the two factors are equal. For any other factor one will be less than sqrt(n) and the other larger. So if we haven't seen one by the time we have checkup up to and including sqrt(n), we won't find one after. – Asoka

Answer 24

We can use java streams to implement this in O(sqrt(n)); Consider that noneMatch is a shortCircuiting method that stops the operation when finds it unnecessary for determining the result:

Scanner in = new Scanner(System.in);
int n = in.nextInt();
System.out.println(n == 2 ? "Prime" : IntStream.rangeClosed(2, ((int)(Math.sqrt(n)) + 1)).noneMatch(a -> n % a == 0) ? "Prime" : "Not Prime");

Camfort

Answer 25

With help of Java-8 streams and lambdas, it can be implemented like this in just few lines:

public static boolean isPrime(int candidate){
        int candidateRoot = (int) Math.sqrt( (double) candidate);
        return IntStream.range(2,candidateRoot)
                .boxed().noneMatch(x -> candidate % x == 0);
    }

Performance should be close to O(sqrt(N)). Maybe someone find it useful.

Ravel

"range" should be replaced with "rangeClosed" to include candidateRoot. Also candidate < 2 case should be handled. – Emrich

How is this different from alirezafnatica's prior answer? – Galvanoscope

Answer 26

Let me suggest you the perfect solution for 64 bit integers. Sorry to use C#. You have not already specified it as python in your first post. I hope you can find a simple modPow function and analyze it easily.

public static bool IsPrime(ulong number)
{
    return number == 2 
        ? true 
        : (BigInterger.ModPow(2, number, number) == 2 
            ? ((number & 1) != 0 && BinarySearchInA001567(number) == false) 
            : false)
}

public static bool BinarySearchInA001567(ulong number)
{
    // Is number in list?
    // todo: Binary Search in A001567 (https://oeis.org/A001567) below 2 ^ 64
    // Only 2.35 Gigabytes as a text file http://www.cecm.sfu.ca/Pseudoprimes/index-2-to-64.html
}

Recrudescence

Answer 27

bool isPrime(int n) {
if(n <= 3)
    return (n > 1)==0? false: true;
else if(n%2 == 0 || n%3 == 0)
    return false;

int i = 5;

while(i * i <= n){
    if(n%i == 0 || (n%(i+2) == 0))
        return false;
    i = i + 6;
}

return true;
}

For any number, the minimum iterations to check if the number is prime or not can be from 2 to square root of the number. To reduce the iterations, even more, we can check if the number is divisible by 2 or 3 as maximum numbers can be eliminated by checking if the number is divisible by 2 or 3. Further any prime number greater than 3 can be expressed as 6k+1 or 6k-1. So the iteration can go from 6k+1 to the square root of the number.

Titmouse

It would be better if you added some explanation to your answer using edit. It might not be clear to many readers why your answer is a good one, and they could learn from you if you explained more. – Yellowwood

Answer 28

### is_prime(number) = 
### if number % p1 !=0 for all p1(prime numbers)  < (sqrt(number) + 1), 
### filter numbers that are not prime from divisors

import math
def check_prime(N, prime_numbers_found = [2]):
    if N == 2:
        return True
    if int(math.sqrt(N)) + 1 > prime_numbers_found[-1]:
        divisor_range = prime_numbers_found + list(range(prime_numbers_found[-1] + 1, int(math.sqrt(N)) + 1+ 1))
    else:
        divisor_range = prime_numbers_found
    #print(divisor_range, N)

    for number in divisor_range:
        if number not in prime_numbers_found:
             if check_prime(number, prime_numbers_found):
                prime_numbers_found.append(number)
                if N % number == 0:
                    return False
        else:
            if N % number == 0:
                return False

    return True

Schadenfreude

How do we know that this is the most compact algorithm? – Horseback

Answer 29

from math import isqrt
def is_prime(n: int) -> bool:
    if n <= 3:
        return n > 1
    if n % 2 == 0 or n % 3 == 0:
        return False
    limit = isqrt(n)
    for i in range(5, limit+1, 6):
        if n % i == 0 or n % (i+2) == 0:
            return False
    return True

Trial Division method.

Woolsey

Your answer could be improved with additional supporting information. Please edit to add further details, such as citations or documentation, so that others can confirm that your answer is correct. You can find more information on how to write good answers in the help center. – Selfcontradiction

Answer 30

When I have to do a fast verification, I write this simple code based on the basic division between numbers lower than square root of input.

def isprime(n):
    if n%2==0:
        return n==2
    else:
        cota = int(n**0.5)+1
        for ind in range(3,2,cota):
            if n%ind==0:
                print(ind)
                return False
    is_one = n==1
    return True != is_one

isprime(22783)

• The last True != n==1 is to avoid the case n=1.

Henryk