Best block size value for block matrix matrix multiplication

Question

I want to do block matrix-matrix multiplication with the following C code.In this approach, blocks of size BLOCK_SIZE is loaded into the fastest cache in order to reduce memory traffic during calculation.

void bMMikj(double **A , double **B , double ** C , int m, int n , int p , int BLOCK_SIZE){

   int i, j , jj, k , kk ;
   register double jjTempMin = 0.0 , kkTempMin = 0.0;

   for (jj=0; jj<n; jj+= BLOCK_SIZE) {
       jjTempMin = min(jj+ BLOCK_SIZE,n); 
       for (kk=0; kk<n; kk+= BLOCK_SIZE) {
           kkTempMin = min(kk+ BLOCK_SIZE,n); 
           for (i=0; i<n; i++) {
               for (k = kk ; k < kkTempMin ; k++) {
                   for (j=jj; j < jjTempMin; j++) {
                      C[i][j]  +=  A[i][k] * B[k][j];
                   }
               }
           }
      }
   }
}

I searched about the best suitable value of BLOCK_SIZE and I found that BLOCK_SIZE <= sqrt( M_fast / 3 ) and M_fast here is L1 cache.

In my computer, I have two L1 cache as shown here with lstopo tool. 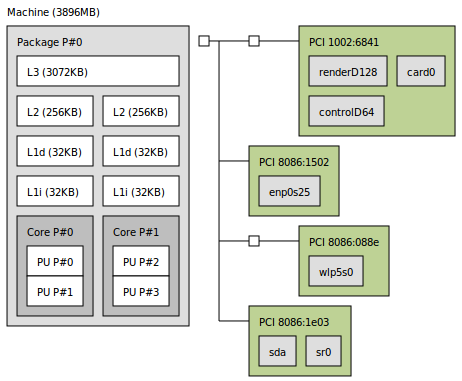Below, I am using heuristics like starting with a BLOCK_SIZE of 4 and increasing the value by 8 for 1000 times, with different values of matrix sizes.

Hopping to get the best MFLOPS ( or the least time for multiplication ) value and the corresponding BLOCK_SIZE value will be the best suitable value.

This is the code for testing:

int BLOCK_SIZE = 4;
int m , n , p;
m = n = p = 1024; /* This value is also changed
                     and all the matrices are square, for simplicity
                     */
for(int i=0;i< 1000; i++ , BLOCK_SIZE += 8) {
    # aClock.start();
    test_bMMikj(A , B ,  C , loc_n , loc_n , loc_n ,BLOCK_SIZE);
    # aClock.stop();
}

Testing gives me different values for each matrix size and do not agree with the formula.The computer model is 'Intel® Core™ i5-3320M CPU @ 2.60GHz × 4 'with 3.8GiB and here is the Intel specification

Another question :
If I have two L1 caches, like what I have in here, should I consider BLOCK_SIZE with respect to one of them or the summation of both?

Ogawa

+1 for checking the CPU-architecture ( NUMA caches ) with lstopo. Unless you disclose the compilation details. no one can tell you more, than that a thread located for code-execution on a physical core P#0 will not benefit from any data located inside L1d belonging to P#1 physical core, so speculations on "shared"-storage start to be valid only from L3 cache ( actually not more than about ~ 3 MB small ). Also always check the actual CPU-cache associativity, cache-line sizes and all the details, that ascertain chances on using the DRAM access-latency masking by cache pre-fetches. – Supererogatory

Thank you. You mean I should only consider L1d and L2d ? Could you please tell me how to check the actual CPU-cache associativity and cache-line sizes? – Ogawa

On x86, CPUID can give you that info at run-time. en.wikipedia.org/wiki/…. (From your cache size / hierarchy, I think you're on a dual-core (with hyperthreading) Intel CPU, like a Haswell i3 desktop or i3/i5 laptop.) If you want this to run fast, as well as cache-blocking, you're going to need your compiler to auto-vectorize it (or manually vectorize with SSE2, AVX, and ideally FMA). With good cache blocking, matmul can more or less saturate the mul/add or FMA throughput even with 32-byte vectors. – Hildegardehildesheim

Yes thank you. I added computer model details – Ogawa

Not sure if this is helpful but I heard that register double is not useful, is that true? – Wish

Answer 1

1. Block Matrix Multiplication: The idea is to make maximum use of both temporal and spatial locality by reusing the data block currently stored in cache. Your code for the same is incorrect as it contains only 5 loops; for block there should be 6, something like :

for(int ii=0; ii<N; ii+=stride)
{
    for(int jj=0; jj<N; jj+=stride)
    {
        for(int kk=0; kk<N; kk+=stride)
        {
            for(int i=ii; i<ii+stride; ++i)
            {
                for(int j=jj; j<jj+stride; ++j)
                {
                    for(int k=kk; k<kk+stride; ++k) C[i][j] += A[i][k]*B[k][j];
                }
            }               
        }
    }
}

Initially keep both N and stride as powers of 2 for simplicity. The ijk pattern is not the most optimal, you should either go for kij or ikj, details on that here. Different access patterns have different performances, you should try all permutations of ijk.

2. Block/Stride size: It is generally said that your fastest cache (L1) should be able to accomodate 3 blocks(stride*stride) of data for optimal performance in case of matrix multiplication, but it's always good to experiment and find it for yourself. Increasing stride by 8 may not be a good idea, try to keep it as increasing powers of 2 because most block sizes are sized in that manner. And you should only look at data cache(L1d) which in your case is 32KB.

Hypnogenesis