What is better, adjacency lists or adjacency matrices for graph problems in C++?

Question

What is better, adjacency lists or adjacency matrix, for graph problems in C++? What are the advantages and disadvantages of each?

Encroach

The structure you use does not depend on the language but on the problem you're trying to solve. – Davedaveda

I meant for general use like djikstra algorithm , i asked this question cause i don't know is linked list implementation worth trying cause it's harder to code than adjacency matrix . – Encroach

Lists in C++ are as easy as typing std::list (or better yet, std::vector). – Davedaveda

@avakar: or std::deque or std::set. It depends on the way the graph will change with time and what algorithms you intend to run on them. – Trinetta

Read details from khan academy – Aesthetic

I find this answer useful as well. – Whity

Answer 1

It depends on the problem.

Adjacency Matrix

• Uses O(n^2) memory
• It is fast to lookup and check for presence or absence of a specific edge
  between any two nodes O(1)
• It is slow to iterate over all edges
• It is slow to add/delete a node; a complex operation O(n^2)
• It is fast to add a new edge O(1)

Adjacency List

• Memory usage depends more on the number of edges (and less on the number of nodes),
  which might save a lot of memory if the adjacency matrix is sparse
• Finding the presence or absence of specific edge between any two nodes
  is slightly slower than with the matrix O(k); where k is the number of neighbors nodes
• It is fast to iterate over all edges because you can access any node neighbors directly
• It is fast to add/delete a node; easier than the matrix representation
• It fast to add a new edge O(1)

Lat

linked lists are harder to code , do you think they the implementation is worth spending some time learning it? – Encroach

@magiix: Yes I think you should understand how to code linked lists if needed, but it's also important to not reinvent the wheel: cplusplus.com/reference/stl/list – Lat

can anyone provide a link with a clean code for say Breadth first search in linked lists format ?? – Encroach

Using std::list geeksforgeeks.org/breadth-first-traversal-for-a-graph – Lurette

The adjacency list can have the same upsides (and none of the downsides) of the adjacency matrix by storing node neighbours in a HashSet. Why use an adjacency matrix at all? – Cumings

Answer 2

This answer is not just for C++ since everything mentioned is about the data structures themselves, regardless of language. And, my answer is assuming that you know the basic structure of adjacency lists and matrices.

Memory

If memory is your primary concern you can follow this formula for a simple graph that allows loops:

An adjacency matrix occupies n²/8 byte space (one bit per entry).

An adjacency list occupies 8e space, where e is the number of edges (32bit computer).

If we define the density of the graph as d = e/n² (number of edges divided by the maximum number of edges), we can find the "breakpoint" where a list takes up more memory than a matrix:

8e > n²/8 when d > 1/64

So with these numbers (still 32-bit specific) the breakpoint lands at 1/64. If the density (e/n²) is bigger than 1/64, then a matrix is preferable if you want to save memory.

You can read about this at wikipedia (article on adjacency matrices) and a lot of other sites.

Side note: One can improve the space-efficiency of the adjacency matrix by using a hash table where the keys are pairs of vertices (undirected only).

Iteration and lookup

Adjacency lists are a compact way of representing only existing edges. However, this comes at the cost of possibly slow lookup of specific edges. Since each list is as long as the degree of a vertex the worst case lookup time of checking for a specific edge can become O(n), if the list is unordered. However, looking up the neighbours of a vertex becomes trivial, and for a sparse or small graph the cost of iterating through the adjacency lists might be negligible.

Adjacency matrices on the other hand use more space in order to provide constant lookup time. Since every possible entry exists you can check for the existence of an edge in constant time using indexes. However, neighbour lookup takes O(n) since you need to check all possible neighbours. The obvious space drawback is that for sparse graphs a lot of padding is added. See the memory discussion above for more information on this.

If you're still unsure what to use: Most real-world problems produce sparse and/or large graphs, which are better suited for adjacency list representations. They might seem harder to implement but I assure you they aren't, and when you write a BFS or DFS and want to fetch all neighbours of a node they're just one line of code away. However, note that I'm not promoting adjacency lists in general.

Amaro

+1 for insight, but this has to be corrected by the actual data structure used to store the adjacency lists. You may want to store for each vertex its adjacency list as a map or a vector, in which case the actual numbers in your formulas have to be updated. Also, similar computations can be used to assess break-even points for time complexity of particular algorithms. – Trinetta

Yeah, this formula is for a specific scenario. If you want a rough answer, go ahead and use this formula, or modify it according to your specifications as needed (for example, most people have a 64 bit computer nowadays :)) – Amaro

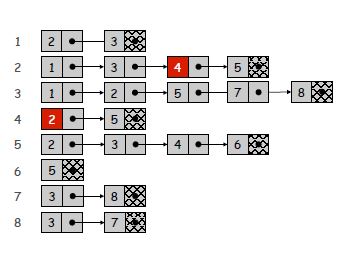
For those interested, the formula for the breaking point (maximum number of average edges in a graph of n nodes) is e = n / s, where s is the pointer size. – Columbous

Answer 3

Okay, I've compiled the Time and Space complexities of basic operations on graphs.
The image below should be self-explanatory.
Notice how Adjacency Matrix is preferable when we expect the graph to be dense, and how Adjacency List is preferable when we expect the graph to be sparse.
I've made some assumptions. Ask me if a complexity (Time or Space) needs clarification. (For example, For a sparse graph, I've taken En to be a small constant, as I've assumed that addition of a new vertex will add only a few edges, because we expect the graph to remain sparse even after adding that vertex.)

Please tell me if there are any mistakes.

Intuitional

In case it is not known if the graph is a dense one or a sparse one, would it be right to say that space complexity for an adjacency list would be O(v+e) ? – Tamworth

For most practical algorithms, one of the most important operations is iterating through all the edges going out of a given vertex. You might want to add it to your list - it's O(degree) for AL and O(V) for AM. – Saury

@johnred isn't it better to say that Adding a vertex (time) for AL is O(1) because instead of O(en) because we don't really add edges on adding a vertex. Adding an edge can be dealt with as a separate operation. For AM it make sense to account but even there we just need to initialize relevant rows and column of new vertex to zero. Addition of edges even for AM can be accounted for separately. – Compete

How is adding a vertex to AL O(V) ? We have to create a new matrix, copy the previous values into it. It should be O(v^2). – Spindle

@Spindle Generally yes, but practically, it depends on the language and on the way it is implemented (you can do a lot of optimizations, and use dynamic arrays for example). – Adeleadelheid

Answer 4

It depends on what you're looking for.

With adjacency matrices you can answer fast to questions regarding if a specific edge between two vertices belongs to the graph, and you can also have quick insertions and deletions of edges. The downside is that you have to use excessive space, especially for graphs with many vertices, which is very inefficient especially if your graph is sparse.

On the other hand, with adjacency lists it is harder to check whether a given edge is in a graph, because you have to search through the appropriate list to find the edge, but they are more space efficient.

Generally though, adjacency lists are the right data structure for most applications of graphs.

Mydriatic

what if you use dictionaries to store the adjacency list, that will give you the presence of an edge in O(1) amortized time. – Uda

Answer 5

Lets assume we have a graph which has n number of nodes and m number of edges,

Example graph

Adjacency Matrix: We are creating a matrix that has n number of rows and columns so in memory it will take space that is proportional to n². Checking if two nodes named as u and v has an edge between them will take Θ(1) time. For example checking for (1, 2) is an edge will look like as follows in the code:

if(matrix[1][2] == 1)

If you want to identify all edges, you have to iterate over matrix at this will require two nested loops and it will take Θ(n²). (You may just use the upper triangular part of the matrix to determine all edges but it will be again Θ(n²))

Adjacency List: We are creating a list that each node also points to another list. Your list will have n elements and each element will point to a list that has number of items that is equal to number of neighbors of this node (look image for better visualization). So it will take space in memory that is proportional to n+m. Checking if (u, v) is an edge will take O(deg(u)) time in which deg(u) equals number of neighbors of u. Because at most, you have to iterate over the list that is pointed by the u. Identifying all edges will take Θ(n+m).

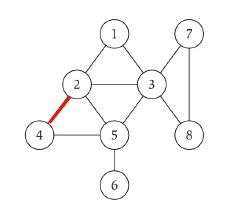
Adjacency list of example graph

You should make your choice according to your needs. Because of my reputation I couldn't put image of matrix, sorry for that

Volkan

What is the orange edge between 2 and 4 in your graph? And why is there no 2 -> 4 or 4 -> 2 in your image? – Assuage

Edge represented as red blocks in the second graph. Second graph represents relation between 2 and 4, 2 has (1, 3, 4, 5) in its list and 4 has (2, 5) in its list. Second graph represents linked list of nodes that the node is connected to. – Volkan

Thanks so much! Came here from SQL and didn't get the linked list thing. – Assuage

Answer 6

If you are looking at graph analysis in C++ probably the first place to start would be the boost graph library, which implements a number of algorithms including BFS.

• Boost Graph Library Docs

EDIT

This previous question on SO will probably help:

how-to-create-a-c-boost-undirected-graph-and-traverse-it-in-depth-first-search

Antananarivo

Thanks you i ll check this library – Encroach

+1 for boost graph. This is the way to go (excepted of course if it's for educational purposes) – Antibiosis

Answer 7

This is best answered with examples.

Think of Floyd-Warshall for example. We have to use an adjacency matrix, or the algorithm will be asymptotically slower.

Or what if it's a dense graph on 30,000 vertices? Then an adjacency matrix might make sense, as you'll be storing 1 bit per pair of vertices, rather than the 16 bits per edge (the minimum that you would need for an adjacency list): that's 107 MB, rather than 1.7 GB.

But for algorithms like DFS, BFS (and those that use it, like Edmonds-Karp), Priority-first search (Dijkstra, Prim, A*), etc., an adjacency list is as good as a matrix. Well, a matrix might have a slight edge when the graph is dense, but only by an unremarkable constant factor. (How much? It's a matter of experimenting.)

Infelicity

For algorithms like DFS and BFS, if you use a matrix then you need to check the whole row each time you want to find adjacent nodes, whereas you already have adjacent nodes in an adjacent list. Why do you think an adjacency list is as good as a matrix in those cases? – Mather

@Mather Exactly, scanning a whole matrix row is an O(n) operation. Adjacency lists are better for sparse graphs when you need to traverse all outgoing edges, they can do that in O(d) (d: degree of the node). Matrices have better cache performance than adjacency lists though, because of sequential access, so for a somewhat dense graphs, scanning a matrices can make more sense. – Alane

Answer 8

To add to keyser5053's answer about memory usage.

For any directed graph, an adjacency matrix (at 1 bit per edge) consumes n^2 * (1) bits of memory.

For a complete graph, an adjacency list (with 64 bit pointers) consumes n * (n * 64) bits of memory, excluding list overhead.

For an incomplete graph, an adjacency list consumes 0 bits of memory, excluding list overhead.

---

For an adjacency list, you can use the follow formula to determine the maximum number of edges (e) before an adjacency matrix is optimal for memory.

edges = n^2 / s to determine the maximum number of edges, where s is the pointer size of the platform.

If you're graph is dynamically updating, you can maintain this efficiency with an average edge count (per node) of n / s.

---

Some examples with 64 bit pointers and dynamic graph (A dynamic graph updates the solution of a problem efficiently after changes, rather than recomputing it from scratch each time after a change has been made.)

For a directed graph, where n is 300, the optimal number of edges per node using an adjacency list is:

= 300 / 64
= 4

If we plug this into keyser5053's formula, d = e / n^2 (where e is the total edge count), we can see we are below the break point (1 / s):

d = (4 * 300) / (300 * 300)
d < 1/64
aka 0.0133 < 0.0156

However, 64 bits for a pointer can be overkill. If you instead use 16bit integers as pointer offsets, we can fit up to 18 edges before breaking point.

= 300 / 16
= 18

d = ((18 * 300) / (300^2))
d < 1/16
aka 0.06 < 0.0625

Each of these examples ignore the overhead of the adjacency lists themselves (64*2 for a vector and 64 bit pointers).

Columbous

I dont't understand the part d = (4 * 300) / (300 * 300), should it not be d = 4 / (300 * 300) ? Since the formula is d = e / n^2 . – Toll

where is the answer of the question? – Conversational

Answer 9

Depending on the Adjacency Matrix implementation the 'n' of the graph should be known earlier for an efficient implementation. If the graph is too dynamic and requires expansion of the matrix every now and then that can also be counted as a downside?

Disembowel

Answer 10

If you use a hash table instead of either adjacency matrix or list, you'll get better or same big-O run-time and space for all operations (checking for an edge is O(1), getting all adjacent edges is O(degree), etc.).

There's some constant factor overhead though for both run-time and space (hash table isn't as fast as linked list or array lookup, and takes a decent amount extra space to reduce collisions).

Saury

Answer 11

I am just going to touch on overcoming the trade-off of regular adjacency list representation, since other answers have covered those aspects.

It is possible to represent a graph in adjacency list with EdgeExists query in amortized constant time, by taking advantage of Dictionary and HashSet data structures. The idea is to keep vertices in a dictionary, and for each vertex, we keep a hash set referencing to other vertices it has edges with.

One minor trade-off in this implementation is that it will have space complexity O(V + 2E) instead of O(V + E) as in regular adjacency list, since edges are represented twice here (because each vertex have its own hash set of edges). But operations such as AddVertex, AddEdge, RemoveEdge can be done in amortized time O(1) with this implementation, except for RemoveVertex, which would be O(V) amortized like in adjacency matrix with an array index lookup dictionary. This would mean that other than implementation simplicity, adjacency matrix don't have any specific advantage. We can save space on sparse graph with almost the same performance in this adjacency list implementation.

Take a look at implementations below in Github C# repository for details. Note that for weighted graph it uses a nested dictionary instead of dictionary-hash set combination so as to accommodate weight value. Similarly for directed graph there is separate hash sets for in & out edges.

Advanced-Algorithms

Note: I believe using lazy deletion we can further optimize RemoveVertex operation to O(1) amortized, even though I haven't tested that idea. For example, upon deletion just mark the vertex as deleted in dictionary, and then lazily clear orphaned edges during other operations.

Alejandrinaalejandro

For adjacency matrix, remove vertex takes O(V^2) not O(V) – Toll

Yes. But if you use a dictionary to track the array indices, then it will go down to O(V). Take a look at this RemoveVertex implementation. – Alejandrinaalejandro