Open CV trivial circle detection -- how to get least squares instead of a contour?

Question

My goal is to accurately measure the diameter of a hole from a microscope. Workflow is: take an image, process for fitting, fit, convert radius in pixels to mm, write to a csv

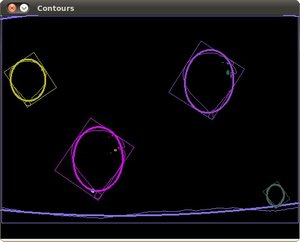
This is an output of my image processing script used to measure the diameter of a hole. I'm having an issue where it seems like my circle fitting is prioritizing matching the contour rather than something like a least squares approach.

I've alternatively averaged many fits in something like this:

My issue here is I like to quickly scan to make sure the circle fit is appropriate. The trade off is the more fits I have, the more realistic the fit, the fewer I have the easier is to make sure the number is correct. My circles aren't always as pretty and circular as this one so it's important to me.

Here's the piece of my script fitting circles if you could take a look and tell me how to do more of a least squares approach on the order of 5 circles. I don't want to use minimum circle detection because a fluid is flowing through this hole so I'd like it to be more like a hydraulic diameter-- thanks!

(thresh, blackAndWhiteImage0) = cv2.threshold(img0, 100, 255, cv2.THRESH_BINARY) #make black + white 
median0 = cv2.medianBlur(blackAndWhiteImage0, 151) #get rid of noise 
circles0 = cv2.HoughCircles(median0,cv2.HOUGH_GRADIENT,1,minDist=5,param1= 25, param2=10, minRadius=min_radius_small,maxRadius=max_radius_small) #fit circles to image

Toddle

minEnclosingCircle and RANSAC circle detection should both be nice for your use case – Pak

"more like a hydraulic diameter" -- from what I read, that's 4x area / circumference. For that you'd just need a contour of the hole (it's not an exact circle anyway, as it appears). Did you examine that approach? – Expecting

Answer 1

Here is another way to fit a circle by getting the equivalent circle center and radius from the binary image using connected components and drawing a circle from that using Python/OpenCV/Skimage.

Input:

import cv2
import numpy as np
from skimage import measure

# load image and set the bounds
img = cv2.imread("dark_circle.png")

# convert to grayscale
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# blur
blur = cv2.GaussianBlur(gray, (3,3), 0)

# threshold
thresh = cv2.threshold(blur, 0, 255, cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU)[1]

# apply morphology open with a circular shaped kernel
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (5,5))
binary = cv2.morphologyEx(thresh, cv2.MORPH_OPEN, kernel, iterations=2)

# find contour and draw on input (for comparison with circle)
cnts = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cnts = cnts[0] if len(cnts) == 2 else cnts[1]
c = cnts[0]
result = img.copy()
cv2.drawContours(result, [c], -1, (0, 255, 0), 1)

# find radius and center of equivalent circle from binary image and draw circle
# see https://scikit-image.org/docs/dev/api/skimage.measure.html#skimage.measure.regionprops
# Note: this should be the same as getting the centroid and area=cv2.CC_STAT_AREA from cv2.connectedComponentsWithStats and computing radius = 0.5*sqrt(4*area/pi) or approximately from the area of the contour and computed centroid via image moments.
regions = measure.regionprops(binary)
circle = regions[0]
yc, xc = circle.centroid
radius = circle.equivalent_diameter / 2.0
print("radius =",radius, "  center =",xc,",",yc)
xx = int(round(xc))
yy = int(round(yc))
rr = int(round(radius))
cv2.circle(result, (xx,yy), rr, (0, 0, 255), 1)

# write result to disk
cv2.imwrite("dark_circle_fit.png", result)

# display it
cv2.imshow("image", img)
cv2.imshow("thresh", thresh)
cv2.imshow("binary", binary)
cv2.imshow("result", result)
cv2.waitKey(0)

Result showing contour (green) compared to circle fit (red):

Circle Radius and Center:

radius = 117.6142467296168   center = 220.2169911178609 , 150.26823599797507

A least squares fit method (between the contour points and a circle) can be obtained using Scipy. For example, see:

https://gist.github.com/lorenzoriano/6799568

https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html

Triclinium

To me, the error between least squares vs a centroid will be smaller than my error from converting pixels to mm. Thanks for the solution I think this is a lot more robust than my script – Toddle

Answer 2

I would suggest computing a mask as in nathancy's answer, but then simply counting the number of pixels in the mask opening that he computed (which is an unbiased estimate of the area of the hole), and then translating the area to a radius using radius = sqrt(area/pi). This will give you the radius of the circle with the same area as the hole, and corresponds to one method to obtain a best fit circle.

A different way of obtaining a best fit circle is to take the contour of the hole (as returned in cnts by cv.findContours in nethancy's answer), finding its centroid, and then computing the mean distance of each vertex to the centroid. This would correspond approximately* to a least squares fit of a circle to the hole perimeter.

^{* I say approximately because the vertices of the contour are an approximation to the contour, and the distances between these vertices is likely not uniform. The error should be really small though.}

---

Here's code example using DIPlib (disclosure: I'm an author) (note: the import PyDIP statement below requires you install DIPlib, and you cannot install it with pip, there is a binary release for Windows on the GitHub page, or otherwise you need to build it from sources).

import PyDIP as dip
import imageio
import math

img = imageio.imread('https://i.sstatic.net/szvc2.jpg')
img = dip.Image(img[:,2600:-1])
img.SetPixelSize(0.01, 'mm')      # Use your actual values!
bin = ~dip.OtsuThreshold(dip.Gauss(img, [3]))
bin = dip.Opening(bin, 25)
#dip.Overlay(img, bin - dip.BinaryErosion(bin, 1, 3)).Show()

msr = dip.MeasurementTool.Measure(dip.Label(bin), features=['Size', 'Radius'])
#print(msr)

print('Method 1:', math.sqrt(msr[1]['Size'][0] / 3.14), 'mm')
print('Method 2:', msr[1]['Radius'][1], 'mm')

The MeasurementTool.Measure function computes 'Size', which is the area; and 'Radius', which returns the max, mean, min and standard deviation of the distances between each boundary pixel and the centroid. From 'Radius', we take the 2nd value, the mean radius.

This outputs:

Method 1: 7.227900647539411 mm
Method 2: 7.225178113501325 mm

But do note that I assigned a random pixel size (0.01mm per pixel), you'll need to fill in the right pixels-to-mm conversion value.

Note how the two estimates are very close. Both methods are good, unbiased estimates. The first method is computationally cheaper.

Hawn

Answer 3

One suggestion I have is looking at cv2.fitEllipse()

Hopefully you can use the aspect ratio between ellipse witdth/height to tell the odd ones out.

Factor

I could then my "diameter" would just be sqr(a*b) – Toddle

taking a look here: docs.opencv.org/2.4/modules/imgproc/doc/… it seems I can only do this with an array of points – Toddle

yes: after you segment your image (filter it so it's easy to separate the hole (foreground) from the background), you use findContours to get these points. In your case you will want simplified external only contours(RETR_EXTERNAL). I would do the following: 1. get the example code I linked to above, 2. swap the image for yours, 3. change findContours arguments (and other arguments) to best fit your image. Once that's done, test with a few more images and tweak for robustness. HTH – Factor

Answer 4

An approach is to Gaussian blur then Otsu's threshold the image to obtain a binary image. From here, we perform morphological opening with a elliptical shaped kernel. This step will effectively remove the tiny noise particles. To obtain a nice estimate of the circle, we find contours and use cv2.minEnclosingCircle() which also gives us the center point and the radius. Here's a visualization:

Input image (screenshoted)

Binary image

Morph open

Result -> Result w/ radius

Radius: 122.11396026611328

From here you can convert the radius in pixels to mm based on your calibration scale

Code

import cv2
import numpy as np

# Load image, convert to grayscale, Gaussian blur, then Otsu's threshold
image = cv2.imread('1.png')
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
blur = cv2.GaussianBlur(gray, (3,3), 0)
thresh = cv2.threshold(blur, 0, 255, cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU)[1]

# Morph open with a elliptical shaped kernel
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (5,5))
opening = cv2.morphologyEx(thresh, cv2.MORPH_OPEN, kernel, iterations=2)

# Find contours and draw minimum enclosing circle
cnts = cv2.findContours(opening, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cnts = cnts[0] if len(cnts) == 2 else cnts[1]
for c in cnts:
    ((x, y), r) = cv2.minEnclosingCircle(c)
    cv2.circle(image, (int(x), int(y)), int(r), (36, 255, 12), 2)
    print('Radius: {}'.format(r))

cv2.imshow('thresh', thresh)
cv2.imshow('opening', opening)
cv2.imshow('image', image)
cv2.waitKey()

Undersecretary

Your output here to me has the same problem as mine in that the 'white' space inside the circle does not equal the 'black' space outside the circle. Towards the bottom they're about equal and then the white space is greater and greater as you move up the circle. That make sense? – Toddle