Calculate object volume with XYZ coordinates

Question

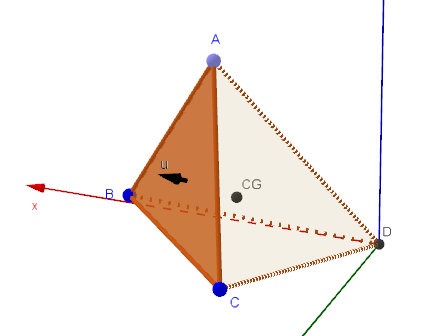
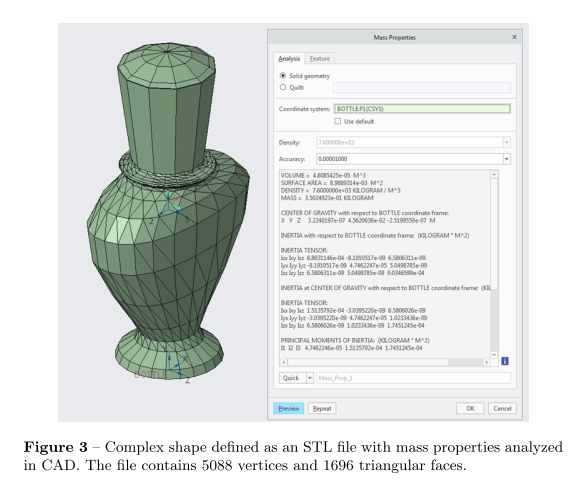
My Winforms app gets a CSV file with XYZ coordinates given from a 3D camera. With these coordinates I need to calculate the object's volume in cubic decimeters (dm3).

I am overwhelmed and not a math expert. I expected to be a library or an algorithm to already do that but the only things I found are in C++ like the PCL library or they use Unity. Is there a simple/clean way for a geometry ignorant guy like me to get the volume of an object with the XYZ coordinates?

UPDATE

This is the fragment of the code I have this far:

public class Volume
{
    //These are only part of the coordinates in the CSV file. There are more than 69.000 lines
    Vector3[] vectors = new Vector3[8]
        {
            new Vector3 {X=-139,Y=-109,Z=285},
            new Vector3 {X=-138,Y=-109,Z=286},
            new Vector3 {X=-136,Y=-109,Z=286},
            new Vector3 {X=-135,Y=-109,Z=286},
            new Vector3 {X=-133,Y=-109,Z=286},
            new Vector3 {X=-132,Y=-109,Z=286},
            new Vector3 {X=-130,Y=-109,Z=286},
            new Vector3 {X=-129,Y=-109,Z=286}
        };

    public double VolumeOfMesh()
    {
        Mesh _mesh = new Mesh();
        double volume = 0.0;

        _mesh.Vertices = vectors; //Should the vectors be organized by proximity to create the triangles?
        _mesh.Triangles = null; //How do I calculate the triangles?

        Vector3[] vertices = _mesh.Vertices;
        int[] triangles = _mesh.Triangles;

        for (int i = 0; i < _mesh.Triangles.Length; i += 3)
        {
            Vector3 p1 = vertices[triangles[i + 0]];
            Vector3 p2 = vertices[triangles[i + 1]];
            Vector3 p3 = vertices[triangles[i + 2]];

            volume += SignedVolumeOfTriangle(p1, p2, p3);
        }

        return Math.Abs(volume);
    }

    private double SignedVolumeOfTriangle(Vector3 p1, Vector3 p2, Vector3 p3)
    {
        var v321 = p3.X * p2.Y * p1.Z;
        var v231 = p2.X * p3.Y * p1.Z;
        var v312 = p3.X * p1.Y * p2.Z;
        var v132 = p1.X * p3.Y * p2.Z;
        var v213 = p2.X * p1.Y * p3.Z;
        var v123 = p1.X * p2.Y * p3.Z;
        return (1.0 / 6.0) * (-v321 + v231 + v312 - v132 - v213 + v123);
    }
}

Should the vectors array be ordered by proximity? How do I populate the Triangles property?

Any advice or guidance will be welcome.

Raggletaggle

But the C# have! Try type "math." (point). – Levey

Gogle search give me library like github.com/gradientspace/geometry3Sharp. But didn't try it. perhaps you could build a minimal reproducible example with a small number of well define 3d point and start from there. Like a simple square. – Megara

I think the solid formed by a triangle and the origin is called a triangular pyramid. – Highspeed

@Dani Pazos Did you manage to solve this problem? Can you share some result code? – Hight

Answer 1

This is how I did this using .STL files which arrange points into triangular faces. In your case, you need to somehow describe which points (nodes) combine to define faces, and to make sure the faces form a closed watertight solid.

The idea is the each three points ABC that form a face together with the origin form a solid of volume

_{where · is the vector dot product, and × the vector cross product.}

It turns out that when you add up all the volumes, some will be positive (facing away from origin) and some negative (facing towards origin). In the end, the sum will equal the enclosed volume of the object.

Here is a sample of the C# code I am using to get solid object properties from a mesh. Remember a mesh is a collection of points called Nodes and a collection of triangles called Faces defined by the three index values of the points in the vertices.

public struct Face3 
{
    public Face3(int indexA, int indexB, int indexC)
    {
        this.IndexA = indexA;
        this.IndexB = indexB;
        this.IndexC = indexC;
    }
    public readonly int IndexA, IndexB, IndexC;
}

public class Mesh3 
{
    public Mesh3(int n_nodes, int n_elements)
    {
        this.Nodes = new Vector3[n_nodes];
        this.Faces = new Face3[n_elements];
    }
    public Mesh3(Vector3[] nodes, Face3[] faces)
    {
        this.Nodes = nodes;
        this.Faces = faces;
    }

    public Vector3[] Nodes { get; }
    public Face3[] Faces { get; }

    public void CalcRigidBodyProperties(double density)
    {
        double sum_vol = 0;
        Vector3 sum_cg = Vector3.Zero;

        for (int i = 0; i < Faces.Length; i++)
        {
            var face = this.Faces[i];

            Vector3 a = this.Nodes[face.IndexA];
            Vector3 b = this.Nodes[face.IndexB];
            Vector3 c = this.Nodes[face.IndexC];

            double face_vol = Vector3.Dot(a, Vector3.Cross(b,c))/6;
            sum_vol += face_vol;

            Vector3 face_cg = (a+b+c)/4;

            sum_cg += face_vol*face_cg;

        }
        // scale volume with density for mass
        var mass = density*sum_vol;
        // find center of mass by dividing by total volume
        var cg = sum_cg / sum_vol;
        ...
    }

    public static Mesh3 FromStl(string filename, double scale = 1)
    {
        // Imports a binary STL file
        // Code Taken From:
        // https://sukhbinder.wordpress.com/2013/12/10/new-fortran-stl-binary-file-reader/
        // Aug 27, 2019
        var fs = File.OpenRead(filename);
        var stl = new BinaryReader(fs);

        var header = new string(stl.ReadChars(80));
        var n_elems = stl.ReadInt32();

        var nodes = new List<Vector3>();
        var faces = new List<Face3>();

        bool FindIndexOf(Vector3 node, out int index)
        {
            for (index = 0; index < nodes.Count; index++)
            {
                if (nodes[index].Equals(node, TrigonometricPrecision))
                {
                    return true;
                }
            }
            index = -1;
            return false;
        }
        for (int i = 0; i < n_elems; i++)
        {
            var normal = new Vector3(
                stl.ReadSingle(),
                stl.ReadSingle(),
                stl.ReadSingle());
            var a = new Vector3(
                scale*stl.ReadSingle(),
                scale*stl.ReadSingle(),
                scale*stl.ReadSingle());
            var b = new Vector3(
                scale*stl.ReadSingle(),
                scale*stl.ReadSingle(),
                scale*stl.ReadSingle());
            var c = new Vector3(
                scale*stl.ReadSingle(),
                scale*stl.ReadSingle(),
                scale*stl.ReadSingle());
            // burn two bytes
            var temp = stl.ReadBytes(2);

            // get index of next point, and add point to list of nodes
            int index_a = nodes.Count;
            nodes.Add(a);
            int index_b = nodes.Count;
            nodes.Add(b);
            int index_c = nodes.Count;
            nodes.Add(c);
            // add face from the three index values
            faces.Add(new Face3( index_a, index_b, index_c ));
        }

        stl.Close();

        return new Mesh3(nodes.ToArray(), faces.ToArray());
    }
}

---

as a test case I used just one triangle defined as follows:

furthermore, I verified the result with a more complex shape (an STL file consisting of many triangles) by comparing the above calculation to that produced by a commercial CAD package.

Highspeed

I updated my question with the code I generated thanks to you answer but I don't know how to achieve this part you comment: "you need to somehow describe which points (nodes) combine to define faces" How should I combien them? By proximity? And how do I populate the triangles property? – Raggletaggle

It depends on what the points represent. I mean, in general a point cloud does not have any structure, but if you can group points together, you might be able to defined surfaces. Then you tessellate the surfaces into triangles. Search for "how to define surfaces from points" and see if anything sticks. – Highspeed

Also search for convex hull calculation, which identifies which points form the outside skin of an object. – Highspeed

@JohnAlexiou Cannot complile your sample code on .NET Framework 4.8: 1) what is frace_vol in CalcRigidBodyProperties function? Is that a mistprint and should be sum_cg += Vector3.Multiply(face_vol, face_cg) 2) what is TrigonometricPrecision in FindIndexOf function? System.Numerics.Vector3.Equals() has only one argument. Moreover FindIndexOf function is not used anywhere.. 3) looks like you need to add int index_a, index_b, index_c; at the beginning of your FromStl function. – Hight

@Hight You are right, there was a typo. As far as Vector3 I am using my own code to work with double values because the precision of float is terrible for this. TrigonometricPrecision is a constant of about 1e-11 that corresponds to the smallest value whose Math.Cos(x)<1. I have my own approximate equals function that uses it. See edits above based on your suggestions. – Highspeed

@Hight - look at this public repo of mine where the volume properties of a mesh are calculated (including the mass moment of inertia tesnor) using System.Numerics.Vectors . Although the precision is terrible. – Highspeed

@JohnAlexiou Where can I see your own code for multiplication of Vector3 by double? And your own approximate Equals function that uses TrigonometricPrecision constant? Thank you in advance. – Hight

@Hight Here is actual definition of trig precision public const double TrigonometricPrecision = 1.0 / 134217728; – Highspeed

@Hight - See Vector3 in JA.SpatialWorld repo. – Highspeed