classification: PCA and logistic regression using sklearn

Question

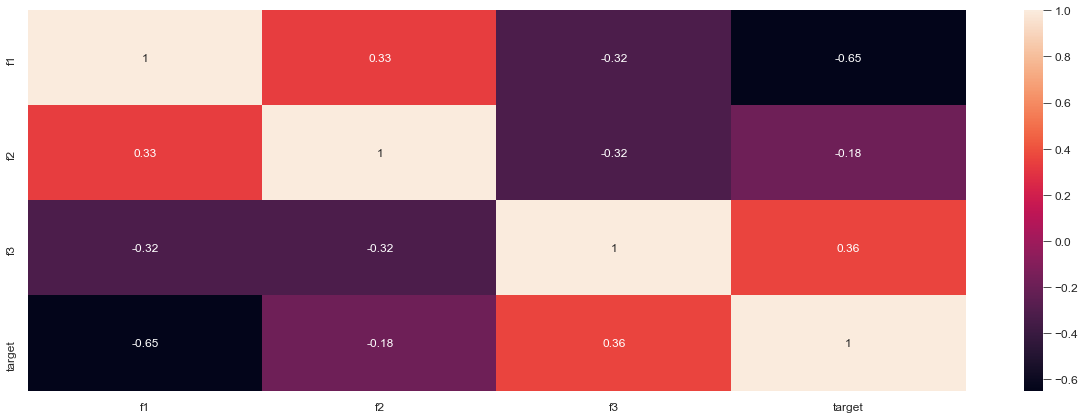
Step 0: Problem description

I have a classification problem, ie I want to predict a binary target based on a collection of numerical features, using logistic regression, and after running a Principal Components Analysis (PCA).

I have 2 datasets: df_train and df_valid (training set and validation set respectively) as pandas data frame, containing the features and the target. As a first step, I have used get_dummies pandas function to transform all the categorical variables as boolean. For example, I would have:

n_train = 10
np.random.seed(0)
df_train = pd.DataFrame({"f1":np.random.random(n_train), \
                         "f2": np.random.random(n_train), \
                         "f3":np.random.randint(0,2,n_train).astype(bool),\
                         "target":np.random.randint(0,2,n_train).astype(bool)})

In [36]: df_train
Out[36]: 
         f1        f2     f3 target
0  0.548814  0.791725  False  False
1  0.715189  0.528895   True   True
2  0.602763  0.568045  False   True
3  0.544883  0.925597   True   True
4  0.423655  0.071036   True   True
5  0.645894  0.087129   True  False
6  0.437587  0.020218   True   True
7  0.891773  0.832620   True  False
8  0.963663  0.778157  False  False
9  0.383442  0.870012   True   True

n_valid = 3
np.random.seed(1)
df_valid = pd.DataFrame({"f1":np.random.random(n_valid), \
                         "f2": np.random.random(n_valid), \
                         "f3":np.random.randint(0,2,n_valid).astype(bool),\
                         "target":np.random.randint(0,2,n_valid).astype(bool)})

In [44]: df_valid
Out[44]: 
         f1        f2     f3 target
0  0.417022  0.302333  False  False
1  0.720324  0.146756   True  False
2  0.000114  0.092339   True   True

I would like now to apply a PCA to reduce the dimensionality of my problem, then use LogisticRegression from sklearn to train and get prediction on my validation set, but I'm not sure the procedure I follow is correct. Here is what I do:

Step 1: PCA

The idea is that I need to transform both my training and validation set the same way with PCA. In other words, I can not perform PCA separately. Otherwise, they will be projected on different eigenvectors.

from sklearn.decomposition import PCA

pca = PCA(n_components=2) #assume to keep 2 components, but doesn't matter
newdf_train = pca.fit_transform(df_train.drop("target", axis=1))
newdf_valid = pca.transform(df_valid.drop("target", axis=1)) #not sure here if this is right

Step2: Logistic Regression

It's not necessary, but I prefer to keep things as dataframe:

features_train = pd.DataFrame(newdf_train)
features_valid = pd.DataFrame(newdf_valid)  

And now I perform the logistic regression

from sklearn.linear_model import LogisticRegression
cls = LogisticRegression() 
cls.fit(features_train, df_train["target"])
predictions = cls.predict(features_valid)

I think step 2 is correct, but I have more doubts about step 1: is this the way I'm supposed to chain PCA, then a classifier ?

Adjudge

I don't see any problem with the procedure. What about your results? Do you get expected output? – Technics

One of the unexpected behavior on my data (different than the example shown here) is that as I increase the number of components in PCA function, my confusion matrix gets worse ! Also, I was wondering if "dummifying" too many categorical variables does not have any effect on the results ? Should I exclude the "target" column during PCA ? – Adjudge

Target is not part of your data. So exclude target labels while using PCA. For categorical data you should use one hot representation implemented in sklearn. – Technics

@Technics thanks! Yes, that's what I did using get_dummies with pandas which is equivalent to one hot encoding. – Adjudge

I don't understand why you need PCA, you have very few features in the dataset. Have you tried to use logistic regression alone? – Dareen

Hi Hoap, indeed in this case, the number of features is very low, but this is not my real dataset (see my comment above). – Adjudge

If you increase the number of components in PCA (and therefore have a lot of features you are using), it is possible to be overfitting your training set and not generalizing properly, hence the confusion matrix results. – Burrell

@Idocao when you are increasing the PCA components, you are actually including more and more information from the original data. If your data features are uncorrelated, then check how much the data is explained by the first principal component alone. (A detailed EDA of the problem is in the answer below). – Sterrett

Answer 1

There's a pipeline in sklearn for this purpose.

from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline

pca = PCA(n_components=2)
clf = LogisticRegression() 

pipe = Pipeline([('pca', pca), ('logistic', clf)])
pipe.fit(features_train, df_train["target"])
predictions = pipe.predict(features_valid)

Piss

what is clf ? is that a typo? – Pronominal

Yup, is should be cls. – Dacia

@Pronominal - clf is short for "classifier", a common abbreviation. – Rutger

Answer 2

PCA is sensitive to the scaling of the variables. To create new dimension it uses the standard deviation of your features. Without scaling the variable importance is biased due to the high/low std. After normalization, all of your features will have the same std and the same weight for PCA when creating reduced space. I'd recommend modifying Alexander Fridman answer:

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline

pca = PCA(n_components=2)
clf = LogisticRegression() 
scaler = StandardScaler()

pipe = Pipeline([('scaler', scaler), ('pca', pca), ('logistic', clf)])
pipe.fit(features_train, df_train["target"])
predictions = pipe.predict(features_valid)

Also n_components is an important parameter that should be tested. In case that you want to do it automatically try:

from sklearn.model_selection import GridSearchCV
param_grid = dict(reduce_dim__n_components=[2,3,4,5])
grid_search = GridSearchCV(estimator=pipe, param_grid=param_grid)
grid_search.fit(features_train, df_train.target)

Messner

Just to add that, if you only center the variables, leave the variances as they are, this is often called "PCA based on covariances". If you also standardize the variables to variances = 1, this is often called "PCA based on correlations", and it can be very different from the former (see a thread here) – Stole

Answer 3

The purpose of PCA is to reduce the dimension of the data so that it is easier to analyze and understand the data - this is done by mapping the data into a different dimension [PCA Basics]. Now, another approach is to find correlations between variables - this can be done by understanding what your underlying data is telling you.

Case Study

Let's understand your problem by taking randomly generated data (as given by you). Before proceeding, there are few points that has to be understood:

1. PCA is sensitive to scaling - so I have used MinMaxScalar from sklearn you can also use StandardScalar (as also pointed out by @Mateusz).
2. It is better to visualize and find if there is any correlation between the data. I have presented a heatmap for the same.

n_train = 10
np.random.seed(0)
df_train = pd.DataFrame({"f1":np.random.random(n_train), \
                         "f2": np.random.random(n_train), \
                         "f3":np.random.randint(0,2,n_train).astype(bool),\
                         "target":np.random.randint(0,2,n_train).astype(bool)})

df_train[df_train.columns] = MinMaxScaler().fit_transform(df_train)

n_valid = 3
np.random.seed(1)
df_valid = pd.DataFrame({"f1":np.random.random(n_valid), \
                         "f2": np.random.random(n_valid), \
                         "f3":np.random.randint(0,2,n_valid).astype(bool),\
                         "target":np.random.randint(0,2,n_valid).astype(bool)})

df_valid[df_valid.columns] = MinMaxScaler().fit_transform(df_valid)

Correlation

For easy understanding, using seaborn as follows:

sns.heatmap(df_train.corr(), annot = True)

There is hardly any correlation but that is expected of randomly generated data.

Application of PCA

As stated, the main purpose is to analyze the data both visually and statistically. So n_components is recommended to be either 2 or 3. However, you can use a scree plot to find the optimal number of components.

Components of PCA

The first principal component (PC-1) explains your data the most, followed by second principal component and so on. Considering all the components - your data is 100% explained - meaning there is statistically no difference between your input data and PCA results with all the components. You can find the explained variance using: pca.explained_variance_ratio_

Considering, n_components = 2 I am creating a dataframe of the PCA results, and appending the target columns, as follows:

pca = PCA(n_components = 2) # fix components
principalComponents = pca.fit_transform(df_train.drop(columns = ["target"]))

PCAResult = pd.DataFrame(principalComponents, columns = [f"PCA-{i}" for i in range(1, 3)])
PCAResult["target"] = df_train["target"].values # data has no bins-column

Out [21]:
     PCA-1        PCA-2    target
0   0.652797    -0.231204   0.0
1   -0.191555   0.206641    1.0
2   0.566872    -0.393667   1.0
3   -0.084058   0.458183    1.0
4   -0.609251   -0.322991   1.0
5   -0.467040   -0.200436   0.0
6   -0.627764   -0.359079   1.0
7   0.075415    0.549736    0.0
8   0.895179    -0.039265   0.0
9   -0.210595   0.332084    1.0

Now, before going further - you have to first check how much the data variance is explained by PCA. If the value is too low - then PCA is not a good choice to train your data (in most of the cases).

Basically, till this point, you have reduced the dimension to 2, and some information is already lost.

Visualizing PCA Results

Now, let's visualize PC-1 vs target using scatterplot:

sns.scatterplot(y = "target", x = "PCA-1", data = PCAResult, s = 225)

Well, there is no logistic relationship between your two variables in the first place.

Similarly, for PC-2 vs target:

Considering PC-1 vs PC-2:

There is some clustering pattern in the data.

Conclusion

You first need to understand if there is any relationship at all. Considering a research output that I am working on, here is a plot between the first principal component PC-1 and the target variable (tan delta):

Clearly, there is some exponential relationship between the data. Once you have established this relationship - you are ready to apply whatever logic you want!!

Sterrett

if there is NO huge multicollinearity - PCA can give strange results instead of clear dimensionality reduction to latent feature space – Herodias