Check when two Vector3 lines intersect - Unity3D

Question

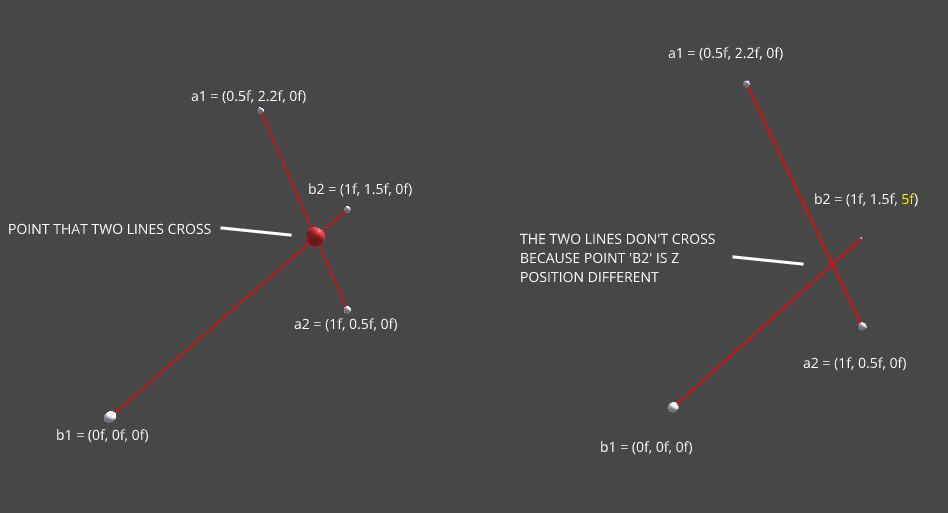
I want to know when four Vector 3 positions intersect, as in the image, from point to point a1 to a2 and b1 to b2 if they intersect each other from each of their positions. Does anyone have any idea how to do this?

Allaallah

This sounds more like a general maths question than c# or unity specific. You could probably rather post it on the Maths page – Covenantor

@Covenantor I'm new to programming, my skills are game design, but I'll be more aware, thanks for the tip – Allaallah

IDEs and game engines often provide functions to calculate answers like these. Thus, posting the question on StackOverflow or the GameDev Stack Exchange is indeed useful for the community – Negrete

Answer 1

The Unity community wiki has a page of math functions that includes a very helpful procedure for this. Copied (and edited slightly) below:

public static bool LineLineIntersection(out Vector3 intersection, Vector3 linePoint1,
        Vector3 lineVec1, Vector3 linePoint2, Vector3 lineVec2){

    Vector3 lineVec3 = linePoint2 - linePoint1;
    Vector3 crossVec1and2 = Vector3.Cross(lineVec1, lineVec2);
    Vector3 crossVec3and2 = Vector3.Cross(lineVec3, lineVec2);

    float planarFactor = Vector3.Dot(lineVec3, crossVec1and2);

    //is coplanar, and not parallel
    if( Mathf.Abs(planarFactor) < 0.0001f 
            && crossVec1and2.sqrMagnitude > 0.0001f)
    {
        float s = Vector3.Dot(crossVec3and2, crossVec1and2) 
                / crossVec1and2.sqrMagnitude;
        intersection = linePoint1 + (lineVec1 * s);
        return true;
    }
    else
    {
        intersection = Vector3.zero;
        return false;
    }
}

So, in your situation, you could use that, then check if the intersection point is between a1 and a2 and b1 and b2:

Vector3 intersection;
Vector3 aDiff = a2-a1;
Vector3 bDiff = b2-b1;
if (LineLineIntersection(out intersection, a1, aDiff, b1, bDiff))
{
    float aSqrMagnitude = aDiff.sqrMagnitude;
    float bSqrMagnitude = bDiff.sqrMagnitude;

    if (    (intersection - a1).sqrMagnitude <= aSqrMagnitude  
         && (intersection - a2).sqrMagnitude <= aSqrMagnitude  
         && (intersection - b1).sqrMagnitude <= bSqrMagnitude 
         && (intersection - b2).sqrMagnitude <= bSqrMagnitude)
    {
        // there is an intersection between the two segments and 
        //   it is at intersection
    }
}

Arbe

While your answer is super useful, through trial and error I found out that Unity's function "Mathf.Approximately(a, b)" doesn't always return a correct value as can be seen on this thread here: https://mcmap.net/q/1478785/-is-mathf-approximately-0-0f-float-epsilon-true-its-correct-behavior ... Therefore sticking to the Unity's community wiki is the solution on this case: "if(Mathf.Abs(planarFactor) < 0.0001f && crossVec1and2.sqrMagnitude > 0.0001f)" – Soelch

The wiki.unity3d link is dead now – Dowry

@PremierBromanov It is intentionally left in the post as a citation. It has been dead for years at this point. – Arbe

Answer 2

You could also use this option if you want to dispense with the UnityEngine library:

1. We define a 2d vector as:

public class V2
    {
        public static V2 zero = new V2(0, 0);

        public readonly float x;
        public readonly float y;

        [JsonConstructor]
        public V2(float x, float y)
        {
            if (
                physicsLogic.debugOn &&
                (float.IsNaN(x) || float.IsNaN(y) || float.IsInfinity(y) || float.IsInfinity(x)))
            {
                throw new Exception($"Dodgy V2 ({x},{y})");
            }

            this.x = x; this.y = y;
        }

        public FieldPoint asFlooredFieldPoint()
        {
            return new FieldPoint(x,0,y);

        }


        public static V2 operator +(V2 b, V2 a) => new V2(b.x + a.x, b.y + a.y);
        public static V2 operator -(V2 b, V2 a) => new V2(b.x - a.x, b.y - a.y);

        public static V2 operator /(V2 a, double b) => new V2((float)(a.x / b), (float)(a.y / b));

        public static V2 operator *(V2 a, double b) => new V2((float)(a.x * b), (float)(a.y * b));
        public static V2 operator *(double b, V2 a) => new V2((float)(a.x * b), (float)(a.y * b));


        [JsonIgnore]
        float mag = -1;

        [JsonIgnore]
        public float magnitude
        {
            get
            {
                if (mag < 0)
                {
                    mag = (float)Math.Sqrt(sqrMagnitude);
                }
                return mag;
            }
        }

        [JsonIgnore]
        public V2 normalized
        {
            get
            {
                var mag = magnitude;

                if (mag == 0)
                {
                    return V2.zero;
                }
                return new V2(x / mag, y / mag);
            }
        }

        [JsonIgnore]
        float _sqrMagnitude = -1;

        [JsonIgnore]
        public float sqrMagnitude
        {
            get
            {
                if (_sqrMagnitude < 0)
                {
                    _sqrMagnitude = (float)(Math.Pow(x, 2) + Math.Pow(y, 2));
                }
                return _sqrMagnitude;
            }
        }

        public override string ToString()
        {
            return $"({x.ToString("F1")},{y.ToString("F1")})";
        }

        public override bool Equals(Object obj)
        {
            //Check for null and compare run-time types.
            if ((obj == null) || !this.GetType().Equals(obj.GetType()))
            {
                return false;
            }
            else
            {
                V2 p = (V2)obj;
                return (MathUtil.closeEnough(x, p.x, .001)) && (MathUtil.closeEnough(y, p.y, .001));
            }
        }

2. We look for the intersection between the two lines, if it exists:

public static V2 intersectSegment(V2 goalStart, V2 goalEnd, V2 ballStart, V2 ballEnd)
        {
            /*  Equations of straight lines 2D: Qx + Ry + S = 0
             *  
             *  The objective is to determine the equations of the straight line of each segment, 
             *  on the one hand the goal line and on the other hand the ball line.
             *  
             *  Then I determine if the two lines intersect at a point, or on the contrary 
             *  if they never intersect, that is, they are parallel.
             *  
             *  If the two lines intersect at a point, I determine the value of that point (P)
             *  
             *  Finally, it is checked if this point is contained in each of the segments.             *  
             *  
             *  
             *  r1: Point A (x_A, y_A); Point B (x_B, y_B) --> AB = (x_B - x_A, y_B - y_A)
             *  r2: Point C (x_C, y_C), Point D (x_D, y_D) --> CD = (x_D - x_C, y_D - y_C)
             * 
             *  r1: (x - x_A)/x_AB = (y - y_A)/y_AB --> r1: Q1x + R1y + S1 = 0
             *  r2: (x - x_C)/x_CD = (y - y_C)/y_CD --> r2: Q2x + R2y + S2 = 0
             *  
             *      ** Q1 = y_AB ; R1 = -x_AB ; S1 = x_AB*y_A - y_AB*x_A
             *      ** Q2 = y_CD ; R2 = -x_CD ; S2 = x_CD*y_C - y_CD*x_C
             * 
             *                    | Q1 R1 |
             *      determinant = | Q2 R2 | = Q1*R2 - Q2*R1
             * 
             *      ** if determinant == 0 -> is parallell
             *      ** if determinant != 0 -> is secant line
             *               
             *  Cut-off point (P):
             *  
             *        Q2*S1 - Q1*S2
             *  y_P = -------------
             *        Q1*R2 - Q2*R1
             *      
             *        S1*(Q2*R1 - Q1*R2) + R1*Q2*(Q1 - S1)
             *  x_P = ------------------------------------
             *               Q1^2*R2 - Q1*Q2*R1
             *  
             *  
             *      ** if P c in AB or CD -> Intersection true
             *  
            */

            var goalVector = goalEnd - goalStart;
            var ballVector = ballEnd - ballStart;

            var Q1 = goalVector.y;
            var Q2 = ballVector.y;

            var R1 = goalVector.x;
            var R2 = ballVector.x;

            var S1 = goalVector.x * goalStart.y - goalVector.y * goalStart.x;
            var S2 = ballVector.x * ballStart.y - ballVector.y * ballStart.x;

            var determinant = Q1 * R2 - Q2 * R1;

            if (determinant != 0)
            {
                var x_P = (S2 * R1 - R2 * S1) / (R2 * Q1 - Q2 * R1);
                var y_P = (S2 * Q1 - Q2 * S1) / (R2 * Q1 - Q2 * R1);

                var intersectPoint = new V2(x_P, y_P);

                if (MathUtil.PointContentInAB(goalStart, goalEnd, intersectPoint ) &&
                    MathUtil.PointContentInAB(ballStart, ballEnd, intersectPoint))
                {
                    return intersectPoint;
                }
            }
            return null;
        }

3. Then, We return true or false if there is such an intersection between the two lines:

public static bool findIfIntersectsInSegment(V2 goalStart, V2 goalEnd, V2 ballStart, V2 ballEnd)
        {            
            return intersectSegment(goalStart,  goalEnd,  ballStart,  ballEnd)!=null;
        }

4. Finally, if the intersection exists, we look for the intersection point of the two lines:

public static bool PointContentInAB(V2 A, V2 B, V2 P)
        {
            /*  Equations of straight lines 2D: Qx + Ry + S = 0
             *  
             *  Point A (x_A, y_A); Point B (x_B, y_B) --> AB = (x_B - x_A, y_B - y_A)
             * 
             *  r1: (x - x_A)/x_AB = (y - y_A)/y_AB --> r1: Q1x + R1y + S1 = 0
             *      Q1 = y_AB ; R1 = -x_AB ; S1 = x_AB*y_A - y_AB*x_A
             *  
             *      ** if P.x <= B.x && P.x >= A.x --> Point content in AB
             */
            var AB = B - A;
            var P_content_in_r1 = AB.y * P.x - AB.x * P.y + (AB.x * A.y - AB.y * A.x);            

            if (nearzero(P_content_in_r1))
            // Point content in r1
            {                
                if (AB.x > 0f)
                {
                    if (P.x <= B.x && P.x >= A.x)
                    // Point content in r1 and AB
                    {
                        if (AB.y > 0f)
                        {
                            if (P.y <= B.y && P.y >= A.y)
                            {
                                return true;
                            }
                        }
                        else
                        {
                            if(P.y >= B.y && P.y <= A.y)
                            {
                                return true;
                            }
                        }
                    }
                }
                else
                {
                    if (P.x >= B.x && P.x <= A.x)
                    {
                        // Point content in r1 and AB
                        if (AB.y > 0f)
                        {
                            if (P.y <= B.y && P.y >= A.y)
                            {
                                return true;
                            }
                        }
                        else
                        {
                            if (P.y >= B.y && P.y <= A.y)
                            {
                                return true;
                            }
                        }
                    }
                }            
            }
            
            return false;

        }

I hope you find it useful, best regards.

Aloin