Finding the ranking of a word (permutations) with duplicate letters

Question

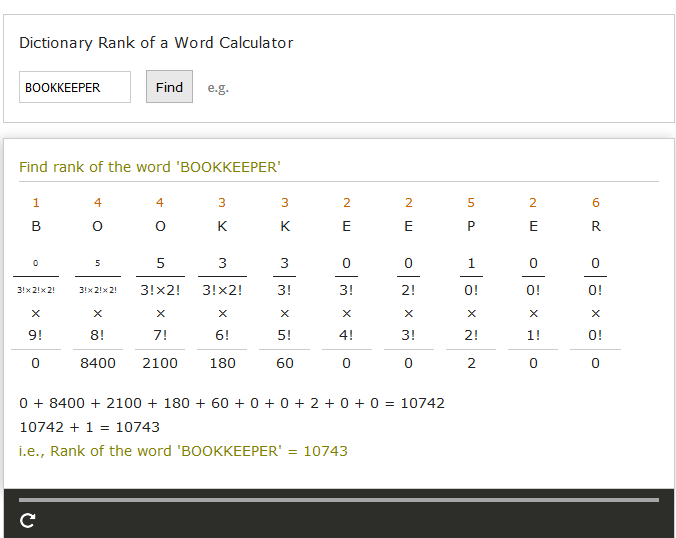
I'm posting this although much has already been posted about this question. I didn't want to post as an answer since it's not working. The answer to this post (Finding the rank of the Given string in list of all possible permutations with Duplicates) did not work for me.

So I tried this (which is a compilation of code I've plagiarized and my attempt to deal with repetitions). The non-repeating cases work fine. BOOKKEEPER generates 83863, not the desired 10743.

(The factorial function and letter counter array 'repeats' are working correctly. I didn't post to save space.)

while (pointer != length)
{
    if (sortedWordChars[pointer] != wordArray[pointer])
    {
        // Swap the current character with the one after that
        char temp = sortedWordChars[pointer];
        sortedWordChars[pointer] = sortedWordChars[next];
        sortedWordChars[next] = temp;
        next++;

        //For each position check how many characters left have duplicates, 
        //and use the logic that if you need to permute n things and if 'a' things 
        //are similar the number of permutations is n!/a!


        int ct = repeats[(sortedWordChars[pointer]-64)];
        // Increment the rank
        if (ct>1) { //repeats?
            System.out.println("repeating " + (sortedWordChars[pointer]-64));
            //In case of repetition of any character use: (n-1)!/(times)!
            //e.g. if there is 1 character which is repeating twice,
            //x* (n-1)!/2!                      
                int dividend = getFactorialIter(length - pointer - 1);
                int divisor = getFactorialIter(ct);
                int quo = dividend/divisor;
                rank += quo;
        } else {
            rank += getFactorialIter(length - pointer - 1);                 
        }                       
    } else
    {
        pointer++;
        next = pointer + 1;
    }
}

Outdare

I take it you want lexicographic ranks? – Cattail

Yes, David - e.g. QUESTION=24572 (works in my code since there are no dupes.) Thanks for the response. – Outdare

Answer 1

Note: this answer is for 1-based rankings, as specified implicitly by example. Here's some Python that works at least for the two examples provided. The key fact is that suffixperms * ctr[y] // ctr[x] is the number of permutations whose first letter is y of the length-(i + 1) suffix of perm.

from collections import Counter

def rankperm(perm):
    rank = 1
    suffixperms = 1
    ctr = Counter()
    for i in range(len(perm)):
        x = perm[((len(perm) - 1) - i)]
        ctr[x] += 1
        for y in ctr:
            if (y < x):
                rank += ((suffixperms * ctr[y]) // ctr[x])
        suffixperms = ((suffixperms * (i + 1)) // ctr[x])
    return rank
print(rankperm('QUESTION'))
print(rankperm('BOOKKEEPER'))

Java version:

public static long rankPerm(String perm) {
    long rank = 1;
    long suffixPermCount = 1;
    java.util.Map<Character, Integer> charCounts =
        new java.util.HashMap<Character, Integer>();
    for (int i = perm.length() - 1; i > -1; i--) {
        char x = perm.charAt(i);
        int xCount = charCounts.containsKey(x) ? charCounts.get(x) + 1 : 1;
        charCounts.put(x, xCount);
        for (java.util.Map.Entry<Character, Integer> e : charCounts.entrySet()) {
            if (e.getKey() < x) {
                rank += suffixPermCount * e.getValue() / xCount;
            }
        }
        suffixPermCount *= perm.length() - i;
        suffixPermCount /= xCount;
    }
    return rank;
}

Unranking permutations:

from collections import Counter

def unrankperm(letters, rank):
    ctr = Counter()
    permcount = 1
    for i in range(len(letters)):
        x = letters[i]
        ctr[x] += 1
        permcount = (permcount * (i + 1)) // ctr[x]
    # ctr is the histogram of letters
    # permcount is the number of distinct perms of letters
    perm = []
    for i in range(len(letters)):
        for x in sorted(ctr.keys()):
            # suffixcount is the number of distinct perms that begin with x
            suffixcount = permcount * ctr[x] // (len(letters) - i)
            if rank <= suffixcount:
                perm.append(x)
                permcount = suffixcount
                ctr[x] -= 1
                if ctr[x] == 0:
                    del ctr[x]
                break
            rank -= suffixcount
    return ''.join(perm)

Cattail

Thanks for the quick reply, David! Let me find a Python hat (I don't know Python) and make some sense out of this elegant looking code. I'll post an update. Thanks again, Max – Outdare

@MaxTomlinson It shouldn't be too hard to transliterate into your language of choice. The loop i in range(len(perm)) steps i from 0 to len(perm) - 1 inclusive by 1. The operator // is truncating division. perm is indexed from 0. The variable ctr is a map from permutation letters to frequencies, where each letter implicitly is initialized to have zero frequency. – Cattail

What threw me a bit is where the for loop ends (implied bracket) so the for loop encompasses up til the return rank. The index through string perm is actually going from end to beginning (right)? The counter is being bumped for each iteration and the 'for y' loop is being done for each iteration, kind of a factorial on the fly? – Outdare

@MaxTomlinson Yes. While rank is being updated, numer * (i + 1) // denom is the number of permutations of the slice of perm consisting of the last i + 1 elements. numer * ctr[y] // denom is the number of permutations that have the same length len(perm) - 1 - i prefix as perm followed by y followed by what's left in some order. Now that I think about it, one could combine numer and denom into one variable. – Cattail

@MaxTomlinson For the revised version: suffixperms is the number of permutations of the length-i suffix. suffixperms * ctr[y] // ctr[x] is the number of permutations of the length-i + 1 suffix that begin with y. – Cattail

I am truly impressed. I've been working on this for days and looked at many posts and none seem to have solved it and you have nailed it so succinctly. The secret (if that is the right word for a problem like this) seems to be in parsing the string from right to left and doing the slicing when I was trying to do factorials. I walked through your code in debug and will have to do it a few more times. Then I want to try and rewrite it on my own. Thanks again. Max – Outdare

@David Eisenstat, pretty cool solution! But your code can't handle very large strings, like 'adsfadfjkzcvzadfadfadfasdfqq', because of int and long overflowing. I know, that one of the solution of this problem is using modular multiplicative inverse, but i don't get how should it be used regarding finding the rank problem. Maybe, you have some idea about handling large strings or know how to use modular multiplicative inverse in this case? – Eh

@Eh Switching to BigInteger would be easiest. Using the Chinese Remainder Theorem here doesn't work because of the less-than test. – Cattail

@David Eisenstat, yes I have already tried with BigInteger, but this is not what I need. For input string 'adsfadfjkzcvzadfadfadfasdfqq' expected output must be 274111 (this value was got with help of modular multiplicative inverse from service for preparing for coding interview), but with BigInteger seems It is impossible to get such output. – Eh

@Eh Ergh, need not to post early in the morning. We're ranking, not unranking. Basically you need to replace the divisions by xCount with multiplications by the modular multiplicative inverse (and perform all arithmetic mod n). – Cattail

@David Eisenstat, thanks for reply. Do you mean replace xCount from this line rank += suffixPermCount * e.getValue() / xCount; or from suffixPermCount /= xCount; or from both? But what is more important is that I don't get what excatly variables I need to use in calculation of modular multiplicative inverse (what value shall I use for "modulus" and what will be "a" and "b"). I checked some math regarding this problem, but i don't understand how should it be used in context of finding rank problem (with large input strings) – Eh

@Eh The modulus is specified by the problem setter on your service. I have no idea what it is. The initial values for the inputs to the extended Euclidean GCD are xCount and the modulus. The output is the coefficient of xCount needed to make 1. – Cattail

@DavidEisenstat: The code is perfect but I am not able to grasp the intuition behind what your code is doing algorithmically to a string. What does finding count of inverse order pair mean? Can you foraward me to maths article of what you are trying to do – Whitt

I have the same inquiries as @Whitt – Prochora

@VictorLin The rank of a perm p is the number of perms q that are less than p. For q to be less than p, they need to agree on the leftmost positions and then disagree where q is lesser. The rest of the perms don't matter for the comparison. The statement rank += ... is counting the number of qs where the first difference is at position i, and the letter of q at i is y (or e.getKey() in the Java version). – Cattail

@DavidEisenstat Can this be reversed as well? Example >>> lexicographic_index('BOOKKEEPER') 229322 then >>> ''.join(list(permutations('BEEEKKOOPR'))[229322]) 'BOOKKEEPER' – Feverwort

@DavidEisenstat Awesome! I made to many mistakes in my attempt, good learning curve :) – Feverwort

Answer 2

If we use mathematics, the complexity will come down and will be able to find rank quicker. This will be particularly helpful for large strings. (more details can be found here)

Suggest to programmatically define the approach shown here (screenshot attached below) given below)

Tini

Cool, but how to retrieve a word from a number rank? – Fattal

Answer 3

I would say David post (the accepted answer) is super cool. However, I would like to improve it further for speed. The inner loop is trying to find inverse order pairs, and for each such inverse order, it tries to contribute to the increment of rank. If we use an ordered map structure (binary search tree or BST) in that place, we can simply do an inorder traversal from the first node (left-bottom) until it reaches the current character in the BST, rather than traversal for the whole map(BST). In C++, std::map is a perfect one for BST implementation. The following code reduces the necessary iterations in loop and removes the if check.

long long rankofword(string s)
{
    long long rank = 1;
    long long suffixPermCount = 1;
    map<char, int> m;
    int size = s.size();
    for (int i = size - 1; i > -1; i--)
    {
        char x = s[i];
        m[x]++;
        for (auto it = m.begin(); it != m.find(x); it++)
                rank += suffixPermCount * it->second / m[x];

        suffixPermCount *= (size - i);
        suffixPermCount /= m[x];
    }
    return rank;
}

Merkley

Answer 4

@Dvaid Einstat, this was really helpful. It took me a WHILE to figure out what you were doing as I am still learning my first language(C#). I translated it into C# and figured that I'd give that solution as well since this listing helped me so much!

Thanks!

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Text.RegularExpressions;

namespace CsharpVersion
{
    class Program
    {
        //Takes in the word and checks to make sure that the word
        //is between 1 and 25 charaters inclusive and only
        //letters are used
        static string readWord(string prompt, int high)
        {
            Regex rgx = new Regex("^[a-zA-Z]+$");
            string word;
            string result;
            do
            {
                Console.WriteLine(prompt);
                word = Console.ReadLine();
            } while (word == "" | word.Length > high | rgx.IsMatch(word) == false);
            result = word.ToUpper();
            return result;
        }

        //Creates a sorted dictionary containing distinct letters 
        //initialized with 0 frequency
        static SortedDictionary<char,int> Counter(string word)
        {
            char[] wordArray = word.ToCharArray();
            int len = word.Length;
            SortedDictionary<char,int> count = new SortedDictionary<char,int>();
           foreach(char c in word)
           {
               if(count.ContainsKey(c))
               {
               }
               else
               {
                   count.Add(c, 0);
               }

           }
           return count;
        }

        //Creates a factorial function
        static int Factorial(int n)
        {
            if (n <= 1)
            {
                return 1;
            }
            else
            {
                return n * Factorial(n - 1);
            }
        }
        //Ranks the word input if there are no repeated charaters 
        //in the word
        static Int64 rankWord(char[] wordArray)
        {
            int n = wordArray.Length; 
            Int64 rank = 1; 
            //loops through the array of letters
            for (int i = 0; i < n-1; i++) 
            { 
                int x=0; 
            //loops all letters after i and compares them for factorial calculation
                for (int j = i+1; j<n ; j++) 
                { 
                    if (wordArray[i] > wordArray[j]) 
                    {
                        x++;
                    }
                }
                rank = rank + x * (Factorial(n - i - 1)); 
             }
            return rank;
        }

        //Ranks the word input if there are repeated charaters
        //in the word
        static Int64 rankPerm(String word) 
        {
        Int64 rank = 1;
        Int64 suffixPermCount = 1;
        SortedDictionary<char, int> counter = Counter(word);
        for (int i = word.Length - 1; i > -1; i--) 
        {
            char x = Convert.ToChar(word.Substring(i,1));
            int xCount;
            if(counter[x] != 0) 
            {
                xCount = counter[x] + 1; 
            }
            else
            {
               xCount = 1;
            }
            counter[x] = xCount;
            foreach (KeyValuePair<char,int> e in counter)
            {
                if (e.Key < x)
                {
                    rank += suffixPermCount * e.Value / xCount;
                }
            }

            suffixPermCount *= word.Length - i;
            suffixPermCount /= xCount;
        }
        return rank;
        }




        static void Main(string[] args)
        {
           Console.WriteLine("Type Exit to end the program.");
           string prompt = "Please enter a word using only letters:";
           const int MAX_VALUE = 25;
           Int64 rank = new Int64();
           string theWord;
           do
           {
               theWord = readWord(prompt, MAX_VALUE);
               char[] wordLetters = theWord.ToCharArray();
               Array.Sort(wordLetters);
               bool duplicate = false;
               for(int i = 0; i< theWord.Length - 1; i++)
               {
                 if(wordLetters[i] < wordLetters[i+1])
                 {
                     duplicate = true;
                 }
               }
               if(duplicate)
               {
               SortedDictionary<char, int> counter = Counter(theWord);
               rank = rankPerm(theWord);
               Console.WriteLine("\n" + theWord + " = " + rank);
               }
               else
               {
               char[] letters = theWord.ToCharArray();
               rank = rankWord(letters);
               Console.WriteLine("\n" + theWord + " = " + rank);
               }
           } while (theWord != "EXIT");

            Console.WriteLine("\nPress enter to escape..");
            Console.Read();
        }
    }
}

Oliviero

Answer 5

If there are k distinct characters, the i^th character repeated n_i times, then the total number of permutations is given by

            (n_1 + n_2 + ..+ n_k)!
------------------------------------------------ 
              n_1! n_2! ... n_k!

which is the multinomial coefficient.
Now we can use this to compute the rank of a given permutation as follows:

Consider the first character(leftmost). say it was the r^th one in the sorted order of characters.

Now if you replace the first character by any of the 1,2,3,..,(r-1)^th character and consider all possible permutations, each of these permutations will precede the given permutation. The total number can be computed using the above formula.

Once you compute the number for the first character, fix the first character, and repeat the same with the second character and so on.

Here's the C++ implementation to your question

#include<iostream>

using namespace std;

int fact(int f) {
    if (f == 0) return 1;
    if (f <= 2) return f;
    return (f * fact(f - 1));
}
int solve(string s,int n) {
    int ans = 1;
    int arr[26] = {0};
    int len = n - 1;
    for (int i = 0; i < n; i++) {
        s[i] = toupper(s[i]);
        arr[s[i] - 'A']++;
    }
    for(int i = 0; i < n; i++) {
        int temp = 0;
        int x = 1;
        char c = s[i];
        for(int j = 0; j < c - 'A'; j++) temp += arr[j];
        for (int j = 0; j < 26; j++) x = (x * fact(arr[j]));
        arr[c - 'A']--;
        ans = ans + (temp * ((fact(len)) / x));
        len--;
    }
    return ans;
}
int main() {
    int i,n;
    string s;
    cin>>s;
    n=s.size();
    cout << solve(s,n);
    return 0;
}

Gibbet

Answer 6

Java version of unrank for a String:

public static String unrankperm(String letters, int rank) {
    Map<Character, Integer> charCounts = new java.util.HashMap<>();
    int permcount = 1;
    for(int i = 0; i < letters.length(); i++) {
        char x = letters.charAt(i);
        int xCount = charCounts.containsKey(x) ? charCounts.get(x) + 1 : 1;
        charCounts.put(x, xCount);

        permcount = (permcount * (i + 1)) / xCount;
    }
    // charCounts is the histogram of letters
    // permcount is the number of distinct perms of letters
    StringBuilder perm = new StringBuilder();

    for(int i = 0; i < letters.length(); i++) {
        List<Character> sorted = new ArrayList<>(charCounts.keySet());
        Collections.sort(sorted);

        for(Character x : sorted) {
            // suffixcount is the number of distinct perms that begin with x
            Integer frequency = charCounts.get(x);
            int suffixcount = permcount * frequency / (letters.length() - i); 

            if (rank <= suffixcount) {
                perm.append(x);

                permcount = suffixcount;

                if(frequency == 1) {
                    charCounts.remove(x);
                } else {
                    charCounts.put(x, frequency - 1);
                }
                break;
            }
            rank -= suffixcount;
        }
    }
    return perm.toString();
}

See also n-th-permutation-algorithm-for-use-in-brute-force-bin-packaging-parallelization.

Hulbert