Crossword solver in PROLOG

Question

The creole of Paradise Island has 14 words: "abandon", "abalone", "anagram", "boat", "boatman", "child", "connect", "elegant", "enhance", "island", "man", "sand", "sun", and "woman".

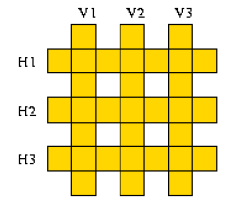
The Paradise Times have published this crossword:

The crossword contains some of the 14 words but no other words.

Write a Prolog program that starts from

word(X) :-
member(X,
[
[a,b,a,n,d,o,n], [a,b,a,l,o,n,e], [a,n,a,g,r,a,m],
[b,o,a,t], [b,o,a,t,m,a,n], [c,h,i,l,d],
[c,o,n,n,e,c,t], [e,l,e,g,a,n,t], [e,n,h,a,n,c,e],
[i,s,l,a,n,d], [m, a, n], [s,a,n,d],
[s,u,n], [w, o, m, a, n]
]).

solution(H1,H2,H3,V1,V2,V3) :-

and defines the predicate solution in such a way that

solution(H1,H2,H3,V1,V2,V3)

is true if and only if H1, H2, H3, V1, V2, and V3 are valid words of Paradise Island which form a valid crossword when written into the grid given above. (For example, the second letter of H1 should coincide with the second letter of V1.)

Use the query

?- solution(H1,H2,H3,V1,V2,V3).

to solve the crossword. Find all solutions to the crossword.

Hint: You might want to start from a smaller crossword and a less rich lexicon.

Skewer

OMG, i'm trying to solve this very same question right now! I cannot believe it! – Debera

Answer 1

Just look at the picture, words are written with letters, you have everything in the picture, translaste it in Prolog lines (my solution has 12 lines, 2 lines for one word).

[EDIT] As every body gives its own solution, here is mine :

solution(H1,H2,H3,V1,V2,V3) :-
    H1 = [_,A2,_,A4,_,A6,_],
    H2 = [_,B2,_,B4,_,B6,_],
    H3 = [_,C2,_,C4,_,C6,_],
    V1 = [_,A2,_,B2,_,C2,_],
    V2 = [_,A4,_,B4,_,C4,_],
    V3 = [_,A6,_,B6,_,C6,_],
    maplist(word, [H1,H2,H3,V1,V2,V3]).

PS I originally wrote word(H1), word(H2) ...

Harlow

I haven't coded in Prolog for 15 years, can't even remember what it looks like, but I'd love to see your solution out of curiosity! – Este

My solution is just for this crossword, it's not a general solution. I just translate what I see. – Harlow

This is the same example i wrote today... However this is not exactly what @Jhonny Tim asked. – Debera

Answer 2

Uniquely domain-selecting select/2 does the trick:

select([A|As],S):- select(A,S,S1),select(As,S1).
select([],_). 
words(X) :- X = [
    [a,b,a,n,d,o,n], [a,b,a,l,o,n,e], [a,n,a,g,r,a,m],
    [b,o,a,t],       [b,o,a,t,m,a,n], [c,h,i,l,d],
    [c,o,n,n,e,c,t], [e,l,e,g,a,n,t], [e,n,h,a,n,c,e],
    [i,s,l,a,n,d],   [m, a, n],       [s,a,n,d],
    [s,u,n],         [w, o, m, a, n]
    ].
solve(Crossword):- words(Words), 
    Crossword = [ [_,A2,_,A4,_,A6,_],
                  [_,B2,_,B4,_,B6,_],
                  [_,C2,_,C4,_,C6,_],
                  [_,A2,_,B2,_,C2,_],
                  [_,A4,_,B4,_,C4,_],
                  [_,A6,_,B6,_,C6,_] ],
    select(Crossword, Words).
solve:- solve(Crossword),
        maplist(writeln, Crossword), writeln(';'), fail 
     ;  writeln('No more solutions!').

Test:

7 ?- solve.
[a, b, a, n, d, o, n]
[e, l, e, g, a, n, t]
[e, n, h, a, n, c, e]
[a, b, a, l, o, n, e]
[a, n, a, g, r, a, m]
[c, o, n, n, e, c, t]
;
[a, b, a, l, o, n, e]
[a, n, a, g, r, a, m]
[c, o, n, n, e, c, t]
[a, b, a, n, d, o, n]
[e, l, e, g, a, n, t]
[e, n, h, a, n, c, e]
;
No more solutions!

This solution only allows for unique words to be used in the puzzle (no duplicates are allowed). This might or might not be what you intended.

Europeanize

Answer 3

Not a Prolog program per se, but a solution using Constraint Logic Programming can be found in Hakan Kjellerstrand's excellent blog on CP. It's in ECLiPSe, but easily adaptable to other Prolog systems with finite domain solvers. Using CLP instead of pure Prolog will make the search much faster.

Illustrator

Answer 4

solution(H1, H2, H3, V1, V2, V3) :-
    crosswordize([H1,H2,H3], [V1,V2,V3]),
    maplist(word, [H1,H2,H3,V1,V2,V3]).

crosswordize([], [[_],[_],[_]]).
crosswordize([[_, X1, _, X2, _, X3, _]|Lines],
             [[_, X1|R1], [_, X2|R2], [_, X3|R3]]) :-
    crosswordize(Lines, [R1,R2,R3]).

The algorithm isn't hard to get:

• we build the grid through the crosswordize/2 predicate call
• we tell prolog that every list is a word

The crosswordize/2 predicate is going through the columns two cells at a time while building lines. If you don't get it you still can "hardcode" it as Will did, it works too!

Earful

are we allowed to use same word more than once in crosswords? I think, usually not. – Europeanize

Well the definition said the crossword is valid if and only if every list a valid paradise thingy word. Since it's an if and only if I do consider the member instead of select call to be valid! – Earful

btw with member/2 I don't have any solution with the same word repeated so one way or the other won't change that many things in this problem :p – Earful

this is a puzzle creator; your version is happy to create crosswords with repeated words, if the lexicon allows. – Europeanize

sure, and as I said it's valid when refering to the definition given... anyway, it's trivial to edit in order not to allow duplicates, it's just a matter of how you read the exercice... – Earful

yes, of course. The select/2 in my answer though just won't select the duplicates in the first place. It's a nice little "paradigm" to use. :) – Europeanize

Answer 5

The theory here is to check for the letters which correspond to themselves in vertical and horizontal words. This can be achieved by using placeholders in the word rule. Checkout this gist https://gist.github.com/ITPol/f8f5418d4f95015b3586 it gives an answer which claims has no repetitions. However, coming from SQL, I think to properly curb repetitions will require a solution along the lines of V1 @< V2; because just using a "not equals to" is just not sufficient enough. Pardon the multiple "[k]nots"; it's actually not that complicated. Pun intended (:

Astrobiology

if we remove the selected item from the pool of available items, there automatically are no repetitions possible. As I show in my answer. (that's what select/3 does). – Europeanize