Neural Network: Solving XOR

Question

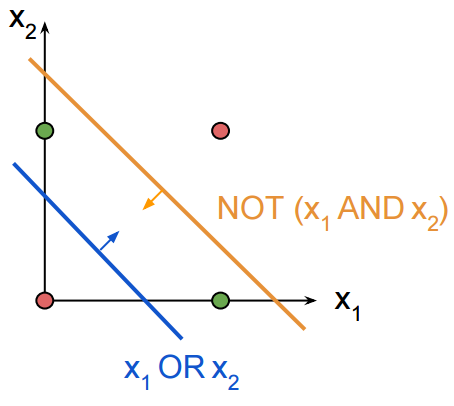
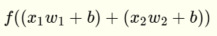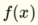Could someone please give me a mathematical correct explanation why a Multilayer Perceptron can solve the XOR problem?

My interpretation of the perceptron is as follows:

A perceptron with two inputs 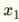and 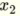has following linear function and is hence able to solve linear separateable problems such as AND and OR.

is the basic step function.

The way I think of it is that I substitute the two parts within 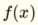separated by the + sign as 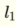and 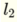and I get 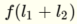which is a line. By applying the step function I get one of the the clusters in respect to the input. Which I interpret as one of the spaces separated by that line.

Because the function of an MLP is still linear, how do I interpret this in a mathematical way and more important: Why is it able to solve the XOR problem when it's still linear? Is it because its interpolating a polynomial?

Fascist

Answer 1

You are looking for a mathematical explanation, so let's first take a look on how a perceptron works:

The input gets weighted and summed up. If it exceeds a threshold theta, 1 is returned, otherwise 0. In the XOR case x1 and x2 can be either 1 or 0 and you are searching for weights w1 and w2 as well as a threshold theta such that in case of x1 XOR x2:

w1*x1 + w2*x2 >= theta

OR

w1*x1 + w2*x2 - theta >= 0

First, you can see that the function is linear. This means that it defines a line. But when you look at the sample space, there is no line that can separate the positive from the negative cases.

Second, you can try it out. Take an arbitrary theta, let's say 0.5.

Case 1: x1 = 1, x2 = 0 => w1 needs to be > 0.5

Case 2: x1 = 0, x2 = 1 => w2 needs to be > 0.5

Case 3: x1 = 1, x2 = 1 => w1+w2 needs to be < 0.5 => impossible due to previous two cases

In general, with a perceptron you can only define functions that are linear separable, i.e. lines, planes, hyperplanes etc.

But for the XOR case you need two lines:

For each line, you need one hidden node and then combine things together while taking the negation into account.

You can see a solution here:

How to solve XOR problem with MLP neural network?

So the trick is not to get non-linear but rewrite XOR into something like:

x1 XOR x2 == NOT (x1 AND x2) AND (x1 OR x2)

Seminal

Yes, i know this. But how comes that by adding a hidden layer and a squashing function it gains the ability to solve the XOR problem? The way I think of it is that it becomes able to interpolate polynomials because it can create many lines that are interconnected at certain points because the function of an MLP is still linear. There is no exponent at all, except for the logistic function...which just squashes the values to a sub space. – Fascist

This really helped me a lot in understanding a Perceptron and the issues/possibilities to deal with the XOR problem, thanks! What would help even more, is to include a graph such as the one for the single layer perceptron, but for a multilayer perceptron that can solve the XOR problem. – Victory

Answer 2

Try plotting the sample space of an XOR function of two variables x₁ and x₂. The decision boundary seperating the positive(y=1) and negative examples(y=0) is clearly not a straight line but a non-linear decision boundary as follows:

Since, modelling a non-linear decision boundary cannot be done by a simple neural network consisting of only input and output layers. Hence, a hidden layer is required to model the non-linear decision boundary required. On the other hand, functions like AND, OR, NOT have linear decision boundary and hence can be modelled by simple input-output neural nets.

Dibru

Answer 3

What perceptron is truly doing is dividing an input space (in case of XOR - a real plane) into two parts separated by an affine subspace of lower dimension (in case of XOR - a line) and assigning different classes to different parts. There is no such a line which divides a plane in that way that points (0,0), (1,1) are separated from (1,0), (0,1).

Multilayer perceptron also divides a input space into two parts but this division is not restricted only to affine separation so it's possible to separate XOR classes.

Cadaverine