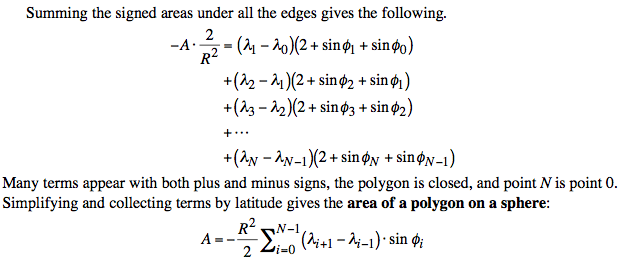Calculate area of MKPolygon in an MKMapView

Question

I just don't know how to calculate the area on the MKMapView. Anyone who has solved this problem yet?

This is my code, but it returns way too much:

func ringArea() -> Double{
    var area: Double = 0

    if templocations.count > 2 {
        var p1,p2:CLLocationCoordinate2D

        for var i = 0; i < templocations.count - 1; i++ {
            var loc = templocations[i] as CLLocation
            p1 = CLLocationCoordinate2D(latitude: loc.coordinate.latitude, longitude: loc.coordinate.longitude)

            loc = templocations[i+1] as CLLocation
            p2 = CLLocationCoordinate2D(latitude: loc.coordinate.latitude, longitude: loc.coordinate.longitude)

            var sinfunc: Float = (2 + sinf(Float(degreeToRadiant(p1.latitude))) + sinf(Float(degreeToRadiant(p2.latitude))))

            area += degreeToRadiant(p2.longitude - p1.longitude) * Double(sinfunc)
        }
        area = area * kEarthRadius * kEarthRadius / 2;
    }
    return area
}

Aborticide

Have you tried to translate https://mcmap.net/q/1086298/-mkpolygon-area-calculation to Swift ? – Hotspur

Answer 1

Stefan's answer implemented in Swift 5.0 :

import MapKit
let kEarthRadius = 6378137.0

func radians(degrees: Double) -> Double {
    return degrees * .pi / 180
}

func regionArea(locations: [CLLocationCoordinate2D]) -> Double {

    guard locations.count > 2 else { return 0 }
    var area = 0.0

    for i in 0..<locations.count {
        let p1 = locations[i > 0 ? i - 1 : locations.count - 1]
        let p2 = locations[i]

        area += radians(degrees: p2.longitude - p1.longitude) * (2 + sin(radians(degrees: p1.latitude)) + sin(radians(degrees: p2.latitude)) )
    }
    area = -(area * kEarthRadius * kEarthRadius / 2)
    return max(area, -area) // In order not to worry about is polygon clockwise or counterclockwise defined.
}

Chuddar

Pardon my ignorance. what units does this return this in? meters? – Denesedengue

@JulianB. Yes! Square meters. If you want something else you need to set up the value of kEarthRadius in the units you need. – Chuddar

@Chuddar where can I get the list of kEarthRadius values? – Clingfish

@avt what are the unit of area? – Verticillate

Answer 2

#define kEarthRadius 6378137
@implementation MKPolygon (AreaCalculation)

- (double) area {
  double area = 0;
  NSMutableArray *coords = [[self coordinates] mutableCopy];
  [coords addObject:[coords firstObject]];

  if (coords.count > 2) {
    CLLocationCoordinate2D p1, p2;
    for (int i = 0; i < coords.count - 1; i++) {
      p1 = [coords[i] MKCoordinateValue];
      p2 = [coords[i + 1] MKCoordinateValue];
      area += degreesToRadians(p2.longitude - p1.longitude) * (2 + sinf(degreesToRadians(p1.latitude)) + sinf(degreesToRadians(p2.latitude)));
    }

    area = - (area * kEarthRadius * kEarthRadius / 2);
  }
  return area;
}
- (NSArray *)coordinates {
  NSMutableArray *points = [NSMutableArray arrayWithCapacity:self.pointCount];
  for (int i = 0; i < self.pointCount; i++) {
    MKMapPoint *point = &self.points[i];
    [points addObject:[NSValue valueWithMKCoordinate:MKCoordinateForMapPoint(* point)]];
  }
  return points.copy;
}

double degreesToRadians(double radius) {
  return radius * M_PI / 180;
}

Enteric

“The Spherical Case” equation is detailed in “Some Algorithms for Polygons on a Sphere” by Chamberlain & Duquette (JPL Publication 07-3, California Institute of Technology, 2007) – Perkoff

@RoselleTanner thank you for the citation, yes, it's exactly that. I was planning to update my answer with the spherical case (in these two years, since my answer, I've forgotten i did in fact implement their spherical algorithm, not the planar one) – Enteric

you used the “The Spherical Case- Approximation” equation. Your article also describes a “The Spherical Case- Exact Solution.” I used the same concepts of spherical excess to implement area. It is posted if you want to take a look at it. – Perkoff

Answer 3

I used spherical excess to calculate the area. The article in StefanS’s answer has a great explanation on how spherical excess works. It uses triangles, with one edge being the polygon segment, and the other two edges are meridians connecting to a pole. Wikipedia suggested using a “spherical quadrangle” with the same principle’s. It uses the polygon segment, the equator, and two edges that are meridians connecting to the equator.

StefanS’s answer uses an equation for the approximation of area. I wanted to be more exact. I implemented 3 different functions. The approximation, the exact spherical triangles, and the exact spherical quadrangles.

The time was negligible in my use case, but here are the baselines:

0.208- approximation time baseline

0.517- exact spherical quadrangles time baseline

0.779- exact spherical triangles time baseline

As a bonus, the quadrangle solution didn’t need any adjustment for the antimeridian, whereas the approximation did. The quadrangle solution is a lot simpler than the triangle solution. In my tests, the largest difference in results between the quadrangle and triangle solutions were about 0.0000001%.

I used this equation from wikipedia's Spherical Trigonometry, Area and Spherical Excess: https://en.wikipedia.org/wiki/Spherical_trigonometry#Area_and_spherical_excess

And StefanS's article: “The Spherical Case” equation is detailed in “Some Algorithms for Polygons on a Sphere” by Chamberlain & Duquette (JPL Publication 07-3, California Institute of Technology, 2007)

func areaUsingQuadrilateralSphericalExcess(_ coordinates: [CLLocationCoordinate2D]) -> Double {
// the poles cannot be in the polygon
    guard coordinates.count > 2 else { return 0 }
    let kEarthRadius = 6378137.0
    var sum = 0.0

    for i in 0..<coordinates.count {
        let p1Latitude = coordinates[i].latitude.degreesToRadians
        let p1Longitude = coordinates[i].longitude.degreesToRadians
        let p2Latitude = coordinates[i + 1].latitude.degreesToRadians
        let p2Longitude = coordinates[i + 1].longitude.degreesToRadians

        let sphericalExcess = 2 * atan((sin(0.5 * (p2Latitude + p1Latitude))/cos(0.5 * (p2Latitude - p1Latitude))) * tan((p2Longitude - p1Longitude)/2))
        sum += sphericalExcess
    }
    return abs(sum * kEarthRadius * kEarthRadius)   // if a clockwise polygon, sum will be negative
}

Perkoff

Love it. Thanks for notifying me! – Enteric

Answer 4

You can still use 2D geometry for calculating surface areas if the dimensions of your area are not so excessive that you need to adjust for the effect of the earth's spheroid.

Assuming that p1 and p2 are less than a few degrees apart and p1 is the centre of the circle and p2 is an arbitrary point on the radius (a radial point), the following function will return the area in square metres.

func findCircleArea(centre: CLLocation, radialLocation: CLLocation) -> Double {
    // Find the distance from the centre to the radial location in metres
    let radius = centre.distanceFromLocation(radialLocation)

    // Apply standard 2D area calculation for a circle
    let area = M_PI * radius * radius

    // Answer is in square metres
    return area
}

If p1 and p2 are both points on the circumference, then use this function instead:

func findCircleAreaBetweenPoints(p1: CLLocation, p2: CLLocation) -> Double {
    // Find the distance from the two points and halve it
    let radius = p1.distanceFromLocation(p2) / 2.0

    // Apply standard 2D area calculation for a circle
    let area = M_PI * radius * radius

    // Answer is in square metres
    return area
}

If you do not use metric measurements, adjust the answer accordingly.

Remember, all surface area calculations are approximations as there are assumptions about the standard WGS84 spheroid as measured at standard sea-level that do not account for variations in elevation at a given location. The distanceFromLocation() calculation uses Great Circle calculations to get the correct distance between points, so the radius reasonably accurate, but when the radius is too large, the error in approximation will also grow.

Sherborn

Okay, thxs for response! Now i have to call findCircleAreaBetweenPoints... for each point? like this? func ringArea(locations: [CLLocation]) -> Double{ var area: Double = 0 if locations.count > 2 { var p1,p2:CLLocationCoordinate2D var i: Int = 0 while i < locations.count-1 { var loc = locations[i] as CLLocation var loc2 = locations[i+1] as CLLocation i++ area += findCircleAreaBetweenPoints(loc, p2: loc2) } } return area } ? – Aborticide

Is it possible, the more locations i have in an area the higher is the error? because if i calculate with all points, the result is definitly wrong, but if always take the 10th value, the result is very good. Is there any limitation of the points in the area? – Aborticide