How do I generate data where points are 'repelled' if they land within a certain proximity to another point?

Question

I'm using runifdisc to plot random points on a disc, but I don't want those points to land within a certain proximity of the other points. The points are currently parsed into squares and triangles. I'm using the spatstat package.

Is there a way to do this? Here is my code:

dots = runifdisc(210, radius=1)
plot(dots, type="n")
points(dots$x[1:45], dots$y[1:45], pch=15, col="red", cex=2)
points(dots$x[46:90], dots$y[46:90], pch=15, col="red", cex=2)
points(dots$x[91:151], dots$y[91:151], pch=17, col="blue", cex=2)
points(dots$x[152:210], dots$y[152:210], pch=17, col="blue", cex=2)

I may even be open to an even distribution of these points, such as on a grid within the disc that I could set the size of, in order to ensure that there is no overlap.

Fluxion

You might want to look up Strauss processes. spatial::Strauss does something like this, although it looks like it only does it in a rectangular domain, so you'd first have to generate the Strauss process on the rectangular domain then subset it to the circular domain. – Guaiacol

Answer 1

You could write your own function to do this. It takes three arguments: the number of points you want, the radius of the containing circle, and the minimum distance between points.

It simply starts with two empty vectors for x and y, then generates a random x, y pair drawn from the uniform distribution. If this x, y pair is outside the unit circle or within a given distance of an existing point, it is discarded and another pair drawn. Otherwise the point is kept. This process is repeated until the x and y vectors are full. At this point, a data frame is created of the x and y values multiplied by the desired circle radius to generate the result.

If it cannot find any places to put a new point after trying a large number of times it will throw an error. The given example of 210 points will only just fit if the minimum distance is 0.1:

repelled_points <- function(n, r_circle, r_clash) {
  container_x <- numeric(n)
  container_y <- numeric(n)
  j <- i <- 1
  while(i <= n)
  {
    j <- j + 1
    if(j == 100 * n) stop("Cannot accommodate the points in given space")
    x <- runif(1, -1, 1)
    y <- runif(1, -1, 1)
    if(x^2 + y^2 > 1) next
    if(i > 1) {
     dist <- sqrt((x - container_x[seq(i-1)])^2 + (y - container_y[seq(i-1)])^2)
     if(any(dist < r_clash)) next
    }
    container_x[i] <- x
    container_y[i] <- y
    i <- i + 1
    j <- 1
  }
  `class<-`(list(window = disc(centre = c(0, 0), radius = r_circle),
       n = n, x = container_x * r_circle, 
       y = container_y * r_circle, markformat = "none"), "ppp")
}

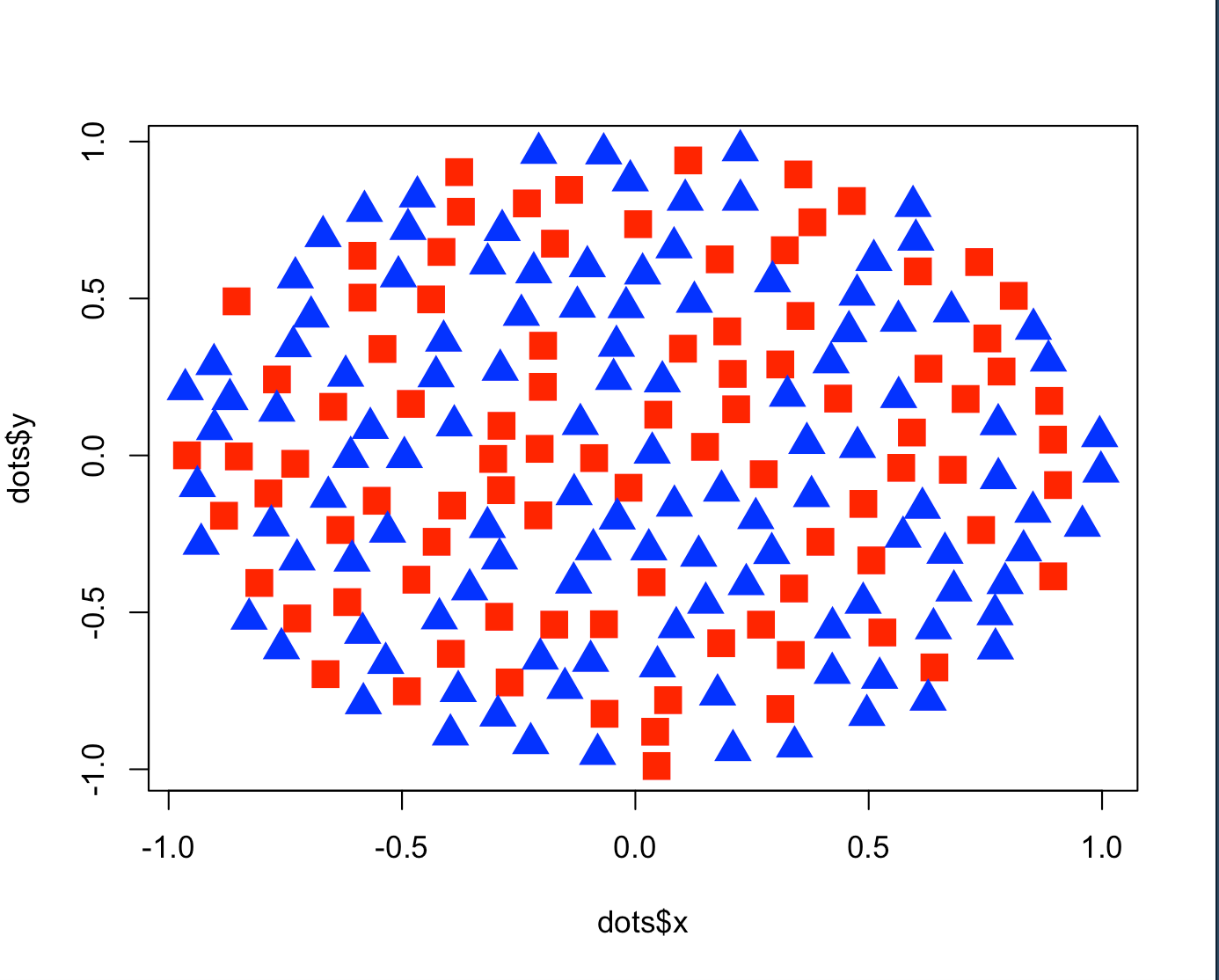
Which, when you run your plotting code, returns the following result:

dots <- repelled_points(210, 1, 0.1)
plot(dots, type="n")
points(dots$x[1:45], dots$y[1:45], pch=15, col="red", cex=2)
points(dots$x[46:90], dots$y[46:90], pch=15, col="red", cex=2)
points(dots$x[91:151], dots$y[91:151], pch=17, col="blue", cex=2)
points(dots$x[152:210], dots$y[152:210], pch=17, col="blue", cex=2)

Dotted

This is Simple Sequential Inhibition, implemented in spatstat as rSSI – Cicelycicenia

Amazing! Thanks so much. I am such a noob, but this helps me learn. This code will give me something to chew on for a while. – Fluxion

Answer 2

There are functions in spatstat to do this, including rSSI, rMaternI, rMaternII, rHardcore, rStrauss and rmh. It depends on how you want the points to "arrive" and how they should be "repelled".

• rSSI: the points arrive one-by-one. Each point is placed randomly, subject to the condition that it does not lie too close to an existing point. The game stops when it is impossible to place a new point anywhere ("simple sequential inhibition")
• rMaternI: the points all arrive at the same time. Then any point which lies too close to another point, is deleted. (Matérn inhibition model 1)
• rMaternII: the points arrive at random times within a certain time period. Their arrival times are recorded. At the end of this period, any point which lies too close to another point, that arrived earlier, is deleted. (Matérn inhibition model 2)
• rHardcore and rmh: the points keep arriving, at random times, forever. A newly-arrived point is rejected and deleted if it falls too close to an existing point. The existing points have finite lifetimes and are deleted at the end of their life. This process is run for a long time and then a snapshot is taken. (Gibbs hard core process simulated using a spatial birth-and-death process).

The functions in spatstat have been thoroughly debugged and tested, so I would recommend using them instead of writing new code, where possible.

For documentation, see Section 5.5 and Chapter 13 of the spatstat book

Cicelycicenia

Answer 3

There are several functions in spatstat to simulate points with a minimum distance. With rHardcore() the points are in a sense independent of each other, but the number of points is random. With rSSI() you get a fixed number of points (if possible before the algorithm gives up):

library(spatstat)
X <- rSSI(0.1, 210, win = disc(1))

You can attach marks randomly to the points to get them plotted with different characters:

marks(X) <- sample(c(rep("a", 90), rep("b", 120)))
plot(X, main = "", cols = c("red", "blue"))

This is not particularly fast.

Evaleen

Nice to find a succinct built-in answer (+1), though this is about 30 times slower than the hand-written function and seems to fail to be able to fit 210 points with the given parameters – Dotted

rSSI performs slowly in your example because it is built to work in a spatial domain of any shape, and does not take advantage of the knowledge that the domain is a disc. If the task was to generate random points in a rectangle, I would expect rSSI to be faster. – Cicelycicenia

The function rSSI has been accelerated in the latest development version of spatstat (1.64-3.009). It now takes about 140 milliseconds to execute. The appropriate command is rSSI(0.1, 210, win=disc(1), giveup=10000) – Cicelycicenia

Answer 4

Not the most elegant solution, but here is an approach

# sample_size = 3000
total_points = 210

find_repelled_dots <- function(total_points, radius = 1, min_distance = 0.1, max_iterations = 10000){
  
  # Initialize the first point
  selected_dots = runifdisc(1, radius=1)
  selected_dots = c(selected_dots$x, selected_dots$y)
  
  # Initialize iterators
  picked = 1
  i = 1
  
  while (picked < total_points & i < max_iterations) { # Either enough points or max iterations
    dots_sample = runifdisc(1, radius = radius) # Choose a data points
    selected_dots_temp = rbind(selected_dots, c(dots_sample$x, dots_sample$y)) # Find distance between existing points
    
    if (min(dist(selected_dots_temp)) > min_distance){ # If sufficiently far from all the other points, add to the mix, else try again
      picked = picked + 1 # Keep track of picked points
      selected_dots = selected_dots_temp # Update picked list
    }
    i = i + 1 # Keep track of iterations
  }
  if (i > 10000){
    stop("Max iterations passed! Increase number of iterations")
  }
  
  return(list(x = selected_dots[,1], y = selected_dots[,2]))
  
}

dots = find_repelled_dots(210)

plot(dots, type="n")
points(dots$x[1:45], dots$y[1:45], pch=15, col="red", cex=2)
points(dots$x[46:90], dots$y[46:90], pch=15, col="red", cex=2)
points(dots$x[91:151], dots$y[91:151], pch=17, col="blue", cex=2)
points(dots$x[152:210], dots$y[152:210], pch=17, col="blue", cex=2)

Hsu

I see that @Allan has a very similar approach - you could try each and see which is faster! – Hsu

using microbenchmark my repelled_points(210, 1, 0.1) completes in an average of 378 milliseconds, and your find_repelled_dots(210) takes over 9 seconds. Still, +1 for a working solution! – Dotted

Thanks for running the benchmarks @AllanCameron - Would suggest to use his solution, wholeheartedly :) – Hsu