2D Bin Packing Algorithm

Question

I have spent some time researching 2d bin packing algorithm. I have no extensive experience in algorithm especially in advanced math but I can code :)

The perfect example of what I need to achieve is demonstrated here http://www.cutlistoptimizer.com. It works, but I can't figure out what algorithm it uses.

I have tried many approaches some of them are very simple like https://codeincomplete.com/posts/bin-packing/ DEMO here, but it doesn't support rotation which is essential.

Most promising for me was https://ssbothwell.github.io/greedypacker-react/ Not sure am I doing something wrong but it doesn't calculate best fit for me. I have tried different combinations with different algorithms.

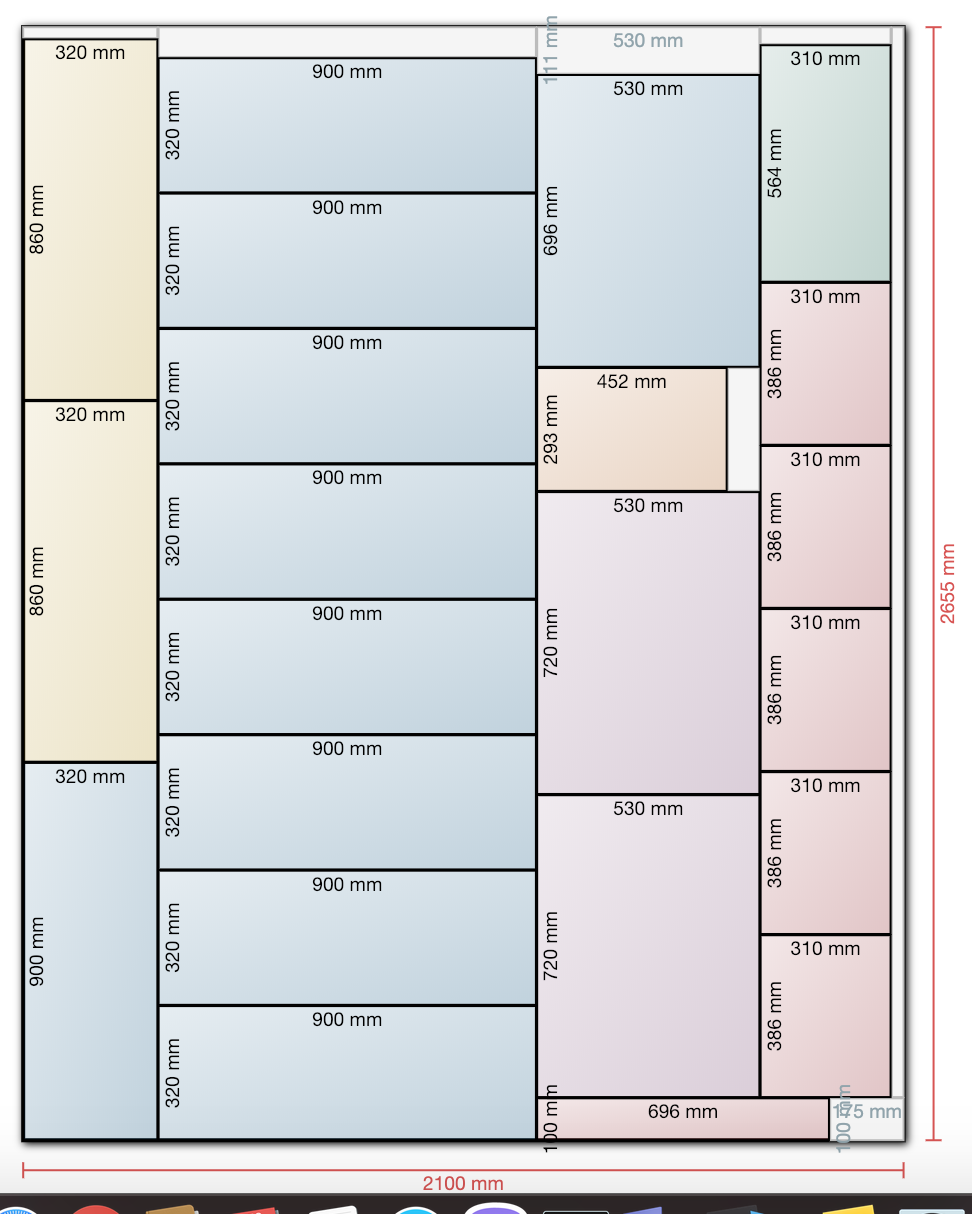
DEMO DATA: Sheet size: w:2655, h: 2100

{ w: 900, h: 320 },
 { w: 320, h: 900 },
 { w: 900, h: 320 },
 { w: 900, h: 320 },
 { w: 900, h: 320 },
 { w: 900, h: 320 },
 { w: 900, h: 320 },
 { w: 900, h: 320 },
 { w: 900, h: 320 },
 { w: 386, h: 310},
 { w: 386, h: 310},
 { w: 386, h: 310},
 { w: 386, h: 310},
 { w: 386, h: 310},
 { w: 860,  h: 320},
 { w: 860,  h: 320},
 { w: 564,  h: 310 },
 { w: 452,  h: 293},
 { w: 720,  h: 530},
 { w: 720,  h: 530},
 { w: 696,  h: 530},
 { w: 696,  h: 100 }

These parts should fit within one sheet.

Reference image

After some time of researching, I have figure out that probably I should use a genetic algorithm in order to evolve these heuristic approaches. Does this make any sense?

Gilcrest

why not rotate the items in advance to get w >= h? – Moo

I can do that, but not sure if that is going to optimize packing. I'll try and let you know. – Gilcrest

@NinaScholz It is not possible to achieve the best result since some parts should have a different rotation like w<h. I have updated original question with the image that explains this behavior. – Gilcrest

Answer 1

You can find this problem in the literature as 2KP, or the 2-Dimensional Knapsack Problem. In your specific case this is 2KP without the orientation constraint (i.e. objects can be rotated).

Sadly this problem falls in the category of problems known as NP-Hard, which means that there is no known polynomial time solution.

Depending on your use case, training a genetic algorithm could be a good solution, probably intermixed with other studied heuristics. Some common heuristics include: filling from the bottom left corner outwards, finding the largest open space and filling with the best fit piece, ordering by levels, etc. Since you are also considering rotation of objects, a logical heuristic is limiting the possible rotations (only 45 degree steps for example).

Two relevant papers:

A Genetic Algorithm for the Two-Dimensional Knapsack Problem with Rectangular Pieces. Andreas Bortfeldt, Tobias Winter

On the two-dimensional Knapsack Problem. Alberto Caprara, Michele Monaci

Illustrative