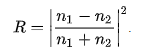How to implement a metallic workflow in PBR?

there is a lot of material out there on the Cook-Torrance BRDF as well as on the Lambert BRDF. Real Shading in Unreal Engine 4 and Moving Frostbite to BPR give an in-depth explanation how to implement them for real-time rendering.

What they omit is the combination of both BRDFs to create the full shading model. If I understand this correctly, we can use at least two basic principles to do that: a specular- and a metalness-workflow. Here is a comparison of them.

I decided to implement the metalness-workflow. So I have the following parameters to base the computation on:

Albedo (RGB)
Roughness (Float)
Metalness (Float)

For the specular part I need to determine my specular color.

Mamoset states that

When using a metalness map, insulative surfaces - pixels set to 0.0 (black) in the metalness map – are assigned a fixed reflectance value (linear: 0.04 sRGB: 0.22) and use the albedo map for the diffuse value. For metallic surfaces – pixels set to 1.0 (white) in the metalness map – the specular color and intensity is taken from the albedo map, and the diffuse value is set to 0 (black) in the shader.

So, the specular color should be calculated by:

vec3 specularColor = mix(vec3(0.04), material.albedo, material.metalness);

Subsequently, this can be used to calculate the reflected radiance. To limit the extend of my question, I will refer to the implementation of Brian Karis here, which is the following:

vec3 L_specular = specularIBL(specularColor, material.roughness, normal, view);

For the diffuse part I need to determine the albedo.

How this works is described in the same quote from above:

vec3 albedo = mix(material.albedo, vec3(0), material.metalness);

Now, the Lambert BRDF can be used to calculate the diffuse lighting from some incoming irradiance E:

vec3 L_diffuse = f_lambert(albedo) * E;

To get the resulting radiance, the diffuse and specular parts are combined:

vec3 L = kd * L_diffuse + ks * L_specular;

My question is how do I calculate kd and ks?

Codinglabs suggests to integrate the fresnel-function over the hemisphere to calculate ks.

kd is afterwards calculated by:

vec3 kd = (1 - ks) * (1 - material.metalness);

The result I'm getting at non-metals is not what I expect when comparing it to the unreal engine for example. The reflection is much lower as expected at normal incidence, which should be due to the low F0 that is set in the case of non-metals. But I checked further sources and 0.04 seems to be the commonly used value.

Can someone confirm the suggested computation of Codinglabs? Or even provide the code Epic uses?

As you've already established, the albedo corresponds to the diffuse colour of the material.

When it comes to the specular, it goes two ways : either dielectric or conductor (typically metallic).

For dielectrics, this is simple, the specular colour is always pure white (no tinting), and is defined by fresnel and the base reflectance (also known as F0) : this scalar simply represents the percentage of light that is reflected when looking at the surface straight on.

The '0.04' value corresponds to a 4% base reflectance, which you can work out by substiting the IOR of 1.5 for n1 in the Fresnel reflectance formula and the IOR of air (approximated to 1.0) for n2 (taken off Wikipedia):

The IOR of a given material is fairly easy to find on the internet, and most dieletrics sit at around 1.5 anyway.

In the case of conductors, the formula isn't quite as straightforward so the usual approach you will find implemented (by Codinglabs, UE4, and other engines) is to explicitely specify a tint/reflectance/specular colour for metallics as it is more artist-friendly. For instance a pure red colour would imply 100% of red light is reflected while 100% of the blue & green light is absorbed.

The metalness term is simply a gross approximation used to interpolate between the explicit artist-specified reflectance colour & the correct/calculated F0 which holds up for dielectrics.

I am not convinced the formula on the link you've posted is quite correct. The law of energy conservation implies that the sum of the diffuse & specular energy be 1.0. As a result, kd should just be :

kd = (1 - ks)

Think of it this way : any light that isn't absorbed by the material should be reflected.

Moreoever, the (1 - material.metalness) is already accounted for when calculating the specular colour :

vec3 specularColor = mix(vec3(0.04), material.albedo, material.metalness);

And for the diffuse colour also :

vec3 albedo = mix(material.albedo, vec3(0), material.metalness);

Where a pure conductor is essentially only specular and no diffusion.

Recommended topics

Hot tags