Replace a chain of image blurs with one blur

Question

In this question I asked how to implement a chain of blurs in one single step.

Then I found out from the gaussian blur page of Wikipedia that:

Applying multiple, successive gaussian blurs to an image has the same effect as applying a single, larger gaussian blur, whose radius is the square root of the sum of the squares of the blur radii that were actually applied. For example, applying successive gaussian blurs with radii of 6 and 8 gives the same results as applying a single gaussian blur of radius 10, since sqrt {6^{2}+8^{2}}=10.

So I thought that blur and singleBlur were the same in the following code:

cv::Mat firstLevel;
float sigma1, sigma2;
//intialize firstLevel, sigma1 and sigma2
cv::Mat blur = gaussianBlur(firstLevel, sigma1);
        blur = gaussianBlur(blur, sigma2);
float singleSigma = std::sqrt(std::pow(sigma1,2)+std::pow(sigma2,2));
cv::Mat singleBlur = gaussianBlur(firstLevel, singleSigma);
cv::Mat diff = blur != singleBLur;
// Equal if no elements disagree
assert( cv::countNonZero(diff) == 0);

But this assert fails (and actually, for example, the first row of blur is different from the first one of singleBlur).

Why?

UPDATE:

After different comments asking for more information, I'll update the answer.

What I'm trying to do is to parallelize this code. In particular, I'm focusing now on computing all the blurs at all levels in advance. The serial code (which works correctly) is the following:

   vector<Mat> blurs ((par.numberOfScales+3)*levels, Mat());
   cv::Mat octaveLayer = firstLevel;
   int scaleCycles = par.numberOfScales+2;

   //compute blurs at all layers (not parallelizable)
   for(int i=0; i<levels; i++){
       blurs[i*scaleCycles+1] = octaveLayer.clone();
       for (int j = 1; j < scaleCycles; j++){
           float sigma = par.sigmas[j]* sqrt(sigmaStep * sigmaStep - 1.0f);
           blurs[j+1+i*scaleCycles] = gaussianBlur(blurs[j+i*scaleCycles], sigma);
           if(j == par.numberOfScales)
               octaveLayer = halfImage(blurs[j+1+i*scaleCycles]);
       }
   }

Where:

Mat halfImage(const Mat &input)
{
   Mat n(input.rows/2, input.cols/2, input.type());
   float *out = n.ptr<float>(0);
   for (int r = 0, ri = 0; r < n.rows; r++, ri += 2)
      for (int c = 0, ci = 0; c < n.cols; c++, ci += 2)
         *out++ = input.at<float>(ri,ci);
   return n;
}

Mat gaussianBlur(const Mat input, const float sigma)
{
   Mat ret(input.rows, input.cols, input.type());
   int size = (int)(2.0 * 3.0 * sigma + 1.0); if (size % 2 == 0) size++;      
   GaussianBlur(input, ret, Size(size, size), sigma, sigma, BORDER_REPLICATE);
   return ret;
}

I'm sorry for the horrible indexes above, but I tried to respect the original code system (which is horrible, like starting counting from 1 instead of 0). The code above has scaleCycles=5 and levels=6, so 30 blurs are generated in total.

This is the "single blur" version, where first I compute the sigmas for each blur that has to be computed (following Wikipedia's formula) and then I apply the blur (notice that this is still serial and not parallelizable):

   vector<Mat> singleBlurs ((par.numberOfScales+3)*levels, Mat());
   vector<float> singleSigmas(scaleCycles);
   float acc = 0;
   for (int j = 1; j < scaleCycles; j++){
       float sigma = par.sigmas[j]* sqrt(sigmaStep * sigmaStep - 1.0f);
       acc += pow(sigma, 2);
       singleSigmas[j] = sqrt(acc);
   }

   octaveLayer = firstLevel;
   for(int i=0; i<levels; i++){
       singleBlurs[i*scaleCycles+1] = octaveLayer.clone();
       for (int j = 1; j < scaleCycles; j++){
           float sigma = singleSigmas[j];
           std::cout<<"j="<<j<<" sigma="<<sigma<<std::endl;
           singleBlurs[j+1+i*scaleCycles] = gaussianBlur(singleBlurs[j+i*scaleCycles], sigma);
           if(j == par.numberOfScales)
               octaveLayer = halfImage(singleBlurs[j+1+i*scaleCycles]);
       }
   }

Of course the code above generates 30 blurs also with the same parameters of the previous version.

And then this is the code to see the difference between each signgleBlurs and blurs:

   assert(blurs.size() == singleBlurs.size());
   vector<Mat> blurDiffs(blurs.size());
   for(int i=1; i<levels*scaleCycles; i++){
        cv::Mat diff;
        absdiff(blurs[i], singleBlurs[i], diff);
        std::cout<<"i="<<i<<"diff rows="<<diff.rows<<" cols="<<diff.cols<<std::endl;
        blurDiffs[i] = diff;
        std::cout<<"blurs rows="<<blurs[i].rows<<" cols="<<blurs[i].cols<<std::endl;
        std::cout<<"singleBlurs rows="<<singleBlurs[i].rows<<" cols="<<singleBlurs[i].cols<<std::endl;
        std::cout<<"blurDiffs rows="<<blurDiffs[i].rows<<" cols="<<blurDiffs[i].cols<<std::endl;
        namedWindow( "blueDiffs["+std::to_string(i)+"]", WINDOW_AUTOSIZE );// Create a window for display.
        //imshow( "blueDiffs["+std::to_string(i)+"]", blurDiffs[i] );                   // Show our image inside it.
        //waitKey(0);                                          // Wait for a keystroke in the window
        Mat imageF_8UC3;
        std::cout<<"converting..."<<std::endl;
        blurDiffs[i].convertTo(imageF_8UC3, CV_8U, 255);
        std::cout<<"converted"<<std::endl;
        imwrite( "blurDiffs_"+std::to_string(i)+".jpg", imageF_8UC3);
   }

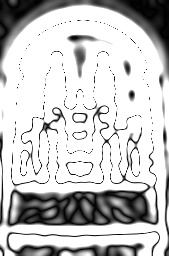
Now, what I've seen is that blurDiffs_1.jpg and blurDiffs_2.jpg are black, but suddendly from blurDiffs_3.jpg until the blurDiffs_29.jpg becomes whiter and whiter. For some reason, blurDiffs_30.jpg is almost completely black.

The first (correct) version generates 1761 descriptors. The second (uncorrect) version generates >2.3k descriptors.

I can't post the blurDiffs matrices because (especially the first ones) are very big and post's space is limited. I'll post some samples. I'll not post blurDiffs_1.jpg and blurDiffs_2.jpg because they're totally blacks. Notice that because of halfImage the images become smaller and smaller (as expected).

blurDiffs_3.jpg:

blurDiffs_6.jpg:

blurDiffs_15.jpg:

blurDiffs_29.jpg:

How the image is read:

  Mat tmp = imread(argv[1]);
  Mat image(tmp.rows, tmp.cols, CV_32FC1, Scalar(0));

  float *out = image.ptr<float>(0);
  unsigned char *in  = tmp.ptr<unsigned char>(0); 

  for (size_t i=tmp.rows*tmp.cols; i > 0; i--)
  {
     *out = (float(in[0]) + in[1] + in[2])/3.0f;
     out++;
     in+=3;
  }

Someone here suggested to divide diff by 255 to see the real difference, but I don't understand why of I understood him correctly.

If you need any more details, please let me know.

Slimy

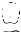
What type is each element in cv::Mat as used in the code? If it's a floating point type then the probability of the diff being precisely zero is very small due to the way floating point values are represented in c++. – Tonneson

@Tonneson No, we are talking about big errors, not the 9-th digit – Slimy

Without considering that I've already done this but...I don't remember how I've done it and I lost the code (shame on me) – Slimy

can you quantify "big errors"? your code does not even compile for me. I can't find any gaussianBlur in the OpenCV documentation. Only GaussianBlur with different parameter list. your sigmas are not initialized with any values... and you have typoes in your code like singleBLur vs singleBlur... – Impassible

Oh you're right, sorry, I updated the question with part of diff (a bunch of 255 with some occasional 0) and the original code (and gaussianBlur) – Slimy

did you try to avoid setting the sigmas and instead only setting the size (and sigmas = zero)? And are you sure it is not just a problem at the image border? Can you output a thresholded difference image for differenr thresholds? imshow((blur - singleBlur) > thres); for thres = 0; 1; 10; 100 for example. Or imwrite. Maybe use absdiff instead of blzr-singleBlur, not sure if it is used implicitly in this case. – Braddy

@Braddy thanks for your comment. I'll update the answer when I'll have done tests, but for now applying the equivalent formula generates more than 2k keypoints instead of 1761, much means (I think) that the problem is relevant. – Slimy

According to Tatarize's answer here math.stackexchange.com/questions/1023984/… the combination of multiple convolutions is od worse speed performance, so maybe you dont want to do it at all... – Braddy

@Braddy What I want to do is the exact opposite: replace a multiple convolutions with a single one. So that's probably going to be faster. – Slimy

that's what I meant by combination. Read the answers in the link. Not sure if it holds for linearly separable filters like faussian blur, but in general it is cheaper to call multiple smaller convolutions than a big one, if I understand it right. – Braddy

@Braddy From wikipedia: "Because of this relationship, processing time cannot be saved by simulating a gaussian blur with successive, smaller blurs — the time required will be at least as great as performing the single large blur." – Slimy

@Braddy I added the code about how the image is read and a bounty for this question. It's crucial for my project. – Slimy

@Tonneson I added a bounty to this question, if you're interested – Slimy

Answer 1

A warning up front: I have no experience with OpenCV, but the following is relevant to computing Gaussian blur in general. And it is applicable as I threw a glance at the OpenCV documentation wrt border treatment and use of finite kernels (FIR filtering).

1. As an aside: your initial test was sensitive to round-off, but you have cleared up that issue and shown the errors to be much larger.

2. Beware image border effects. For pixels near the edge, the image is virtually extended using one of the offered methods (BORDER_DEFAULT, BORDER_REPLICATE, etc...). If your image is |abcd| and you use BORDER_REPLICATE you are effectively filtering an extended image aaaa|abcd|dddd. The result is klmn|opqr|stuv. There are new pixel values (k,l,m,n,s,t,u,v) that are immediately discarded to yield the output image |opqr|. If you now apply another Gaussian blur, this blur will operate on a newly extended image oooo|opqr|rrrr - different from the "true" intermediate result and thus giving you a result different from that obtained by a single Gaussian blur with a larger sigma. These extension methods are safe though: REFLECT, REFLECT_101, WRAP.

3. Using a finite kernel size the G(s1)*G(s2)=G(sqrt(s1^2+s2^2)) rule does not hold in general due to the tails of the kernel being cut off. You can reduce the error thus introduced by increasing the kernel size relative to the sigma, e.g.:

   int size = (int)(2.0 * 10.0 * sigma + 1.0); if (size % 2 == 0) size++;
   

Point 3 seems to be the issue that is "biting" you. Do you really care whether the G(s1)*G(s2) property is preserved. Both results are wrong in a way. Does it affect the methodology that works on the result in a major way? Note that the example of using 10x sigma I have given may resolve the difference, but will be very much slower.

Update: I forgot to add what might the most practical resolution. Compute the Gaussian blur using a Fourier transform. The scheme would be:

• Compute Fourier transform (FFT) of your input image
• Multiply with the Fourier transform of the Gaussian kernel and compute inverse Fourier transform. Ignore the imaginary part of the complex output.

You can find the equation for the Gaussian in the frequency domain on wikipedia

You can perform the second step separately (i.e. in parallel) for each scale (sigma). The border condition implied computing the blur this way is BORDER_WRAP. If you prefer you can achieve the same but with BORDER_REFLECT if you use a discrete cosine transform (DCT) instead. Do not know if OpenCV provides one. You will be after the DCT-II

Pericope

Answer 2

It's basically as what G.M. says. Remember you are not only rounding by floating points, you are also rounding by looking only at integer points (both on the image and on the Gaussian kernels).

Here's what I got from a small (41x41) image:

where blur and single are rounded by convertTo(...,CV8U) and diff is where they are different. So, in DSP terms, it may not be a great agreement. But in Image Processing, it's not that bad.

Also, I suspect that the different will be less significant as you perform Gaussian on bigger images.

Nakamura

I noticed that by using BORDER_DEFAULT instead of BORDER_REPLICATE the result is perfectly the same, even though the final result is worse and even slower... – Slimy

I was wrong, it doesn't work neither by using BORDER_DEFAULT – Slimy

Btw this method looks wrong: by using multiple blurs I correctly detect 1761 keypoints, instead with this method I detect more than 2k, which is obviously wrong – Slimy

I updated the question with many more details and sample images. Please give a look at it. – Slimy

Do you have any idea why this happens? I'm really stucked here and I can't continue my project otherwise – Slimy

I added the code about how the image is read and a bounty for this question. It's crucial for my project. – Slimy