How to write an algorithm to calculate the occlusion percentage of a sphere by another sphere when viewed from a point?

Question

Language doesn't matter all that much since this is an algorithm problem, but let's say I'm using Python 3.

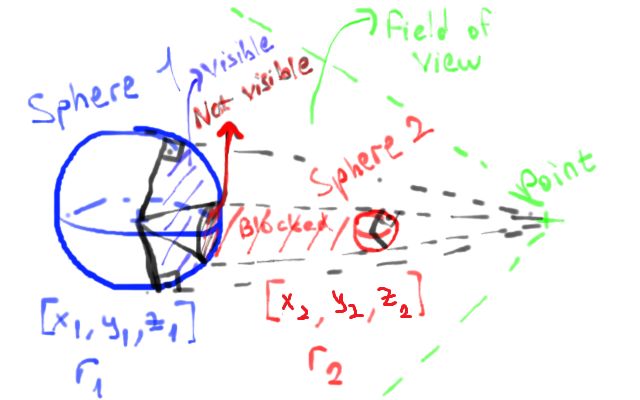
Imagine there are two spheres in a 3D space. The spheres have a center position [x, y, z] and a radius r. I also have a point in the same space, at some known position [x, y, z].

# a simple sample code
class sphere:
   def __init__(self, pos, r):
      self.pos = pos # a list of 3 floats, [x, y, z]
      self.r = r     # a float

class point:
   def __init__(self, pos):
      self.pos = pos # a list of 3 floats, [x, y, z]

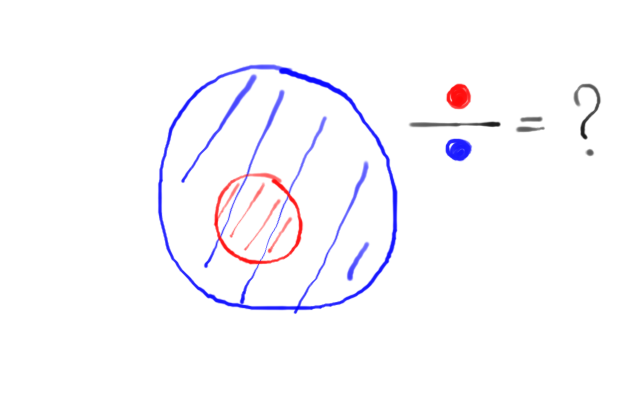
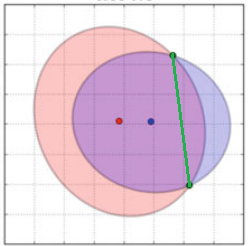
Imagine an observer at the point, with wide enough field of view (this is obviously perspective view, since rays meet at a single point) to see the entirety of both spheres. However, one of the spheres eclipses (occludes) the other.

I need to find the ratio of the occluded area on the farther away sphere compared to the entire area that would've been visible without the second sphere which is blocking the view. I need help with figuring out how to write this algorithm.

Please do not suggest packages that would do this calculation for me out-of-the-box.

For clarity, I'm after the projected view area on a viewing plane.

Clamorous

Is the occluding sphere wholly "inside" the blocked sphere ? Are you after the projected area on some viewing plane or after the remaining area of the cap in 3D ? These are very different problems. – Paramorph

The occluding sphere is not necessarily completely "inside" the sphere in the background. I'm after the projected area on a viewing plane. – Cirilo

Please specify the viewing plane. – Paramorph

Does not matter, perspective view with any fov large enough and any near and far Z planes that contain the spheres are okay. – Cirilo

Answer 1

The 3D problem is quite arduous.

WLOG, the viewing point is the origin, the occluding sphere with center at (0, 0, d) radius r, and the occluded sphere has the center (U, 0, Z) and radius R. (If not, by a change of basis you can always achieve that.)

Now the viewing cone of the occluding sphere has the implicit equation

X² + Y² = k² Z²

and the occluded sphere

(X - U)² + Y² + (Z - V)² = R².

By subtraction,

- 2 U X + U² + (1 - k²) Z² - 2 V Z + V² = R²

gives X as a quadratic function of Z, and from this, Y as a the square root of a quartic function of Z in.

Getting the area of the cap of the sphere delimited by this curve seems hopeless.

Paramorph

Answer 2

Hints:

The 2D case (projection onto a viewing plane) is more tractable, but not trivial.

A sphere viewed in perspective is seen as an ellipse. (It is the intersection of the viewing plane and a cone tangent to the sphere.) Some more insight here: https://math.stackexchange.com/questions/1367710/perspective-projection-of-a-sphere-on-a-plane

If the occluding sphere projects "inside" the occluded one, it suffices to compute the difference of the areas, given by πab.

Otherwise, you need to find the intersection points between the ellipses (two or four of them). This takes the resolution of a quartic equation, for which explicit formulas are known, but complicated.

In the case of two intersection points, you can compute the areas of the elliptic segments delimited by the line segment that joins them (by stretching the ellipse to make it a circle you get a circular segment, for which we have the formula). Finally, you subtract from the occluded ellipse its segment and the complementary segment of the occluding ellipse, to get a crescent.

More here: https://digitalcommons.calpoly.edu/cgi/viewcontent.cgi?referer=&httpsredir=1&article=1016&context=stat_fac

---

Derivation of the equation of the projection of a sphere:

Assume a sphere centered at (U, V, W), with radius R. We take the viewing plane Z=F and the projection center at the origin. Hence the parametric equation of a ray is t.(X, Y, F). We plug this in the equation of the sphere and express that the ray is tangent to the sphere:

(t.X - U)² + (t.Y - V)² + (t.F - W)² = R²,

which must have a null discriminant. So,

(X.U + Y.V + F.W)² = (X² + Y² + F²).(U² + V² + W² - R²)

which is the equation of a conic. Center and reduce to find the axes.

---

To intersect two conics, you can use the traditional technique of creating a pencil, finding a degenerate conic in the pencil and factoring it. Alternatively, there is always a linear transformation (based on the ellipse axis) that turns one of the ellipses to the reduced form X²+Y²=1.

Then, by plugging the Weierstrass parameterization of the circle X=(1-t²)/(1+t²), Y=2t/(1+t²) in the equation of the other conic, you directly obtain the quartic equation

a(1-t²)² + 2b(1-t²)t + 4ct² + d(1-t²)(1+t²) + 2et(1+t²) + f(1+t²)² = 0.

Paramorph