Compute a confidence interval from sample data assuming unknown distribution

Question

I have sample data for which I would like to compute a confidence interval, assuming a distribution that is not normal and is unknown. Basically, it looks like the distribution is Pareto. But I don't know for sure.

The answers for the normal distribution:

Compute a confidence interval from sample data

Correct way to obtain confidence interval with scipy

Heuer

Answer 1

If you don't know the underlying distribution, then my first thought would be to use bootstrapping: https://en.wikipedia.org/wiki/Bootstrapping_(statistics)

In pseudo-code, assuming x is a numpy array containing your data:

import numpy as np
N = 10000
mean_estimates = []
for _ in range(N):
    re_sample_idx = np.random.randint(0, len(x), x.shape)
    mean_estimates.append(np.mean(x[re_sample_idx]))

mean_estimates is now a list of 10000 estimates of the mean of the distribution. Take the 2.5th and 97.5th percentile of these 10000 values, and you have a confidence interval around the mean of your data:

sorted_estimates = np.sort(np.array(mean_estimates))
conf_interval = [sorted_estimates[int(0.025 * N)], sorted_estimates[int(0.975 * N)]]

Caput

I have tested with real data.. look like wrong. I got Conf Int: [22.78, 69.93] . (np.array(x) < 22.79).sum() / len(x) - 0.91. 91% of data is below lower conf bound. Arithmetic mean is 40.78 - that is tricky real world data set. – Heuer

Answer 2

You can use bootstrap to approximate every quantity also coming from unknown distributions

def bootstrap_ci(
    data, 
    statfunction=np.average, 
    alpha = 0.05, 
    n_samples = 100):

    """inspired by https://github.com/cgevans/scikits-bootstrap"""
    import warnings

    def bootstrap_ids(data, n_samples=100):
        for _ in range(n_samples):
            yield np.random.randint(data.shape[0], size=(data.shape[0],))    
    
    alphas = np.array([alpha/2, 1 - alpha/2])
    nvals = np.round((n_samples - 1) * alphas).astype(int)
    if np.any(nvals < 10) or np.any(nvals >= n_samples-10):
        warnings.warn("Some values used extremal samples; results are probably unstable. "
                      "Try to increase n_samples")

    data = np.array(data)
    if np.prod(data.shape) != max(data.shape):
        raise ValueError("Data must be 1D")
    data = data.ravel()
    
    boot_indexes = bootstrap_ids(data, n_samples)
    stat = np.asarray([statfunction(data[_ids]) for _ids in boot_indexes])
    stat.sort(axis=0)

    return stat[nvals]

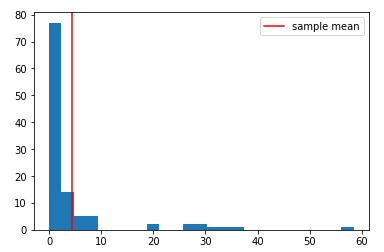
Simulate some data from a pareto distribution:

np.random.seed(33)
data = np.random.pareto(a=1, size=111)
sample_mean = np.mean(data)

plt.hist(data, bins=25)
plt.axvline(sample_mean, c='red', label='sample mean'); plt.legend()

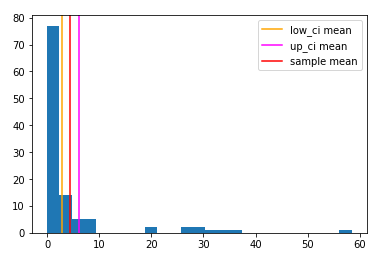
Generate confidence intervals for the SAMPLE MEAN with bootstrapping:

low_ci, up_ci = bootstrap_ci(data, np.mean, n_samples=1000)

plot the resuts

plt.hist(data, bins=25)
plt.axvline(low_ci, c='orange', label='low_ci mean')
plt.axvline(up_ci, c='magenta', label='up_ci mean')
plt.axvline(sample_mean, c='red', label='sample mean'); plt.legend()

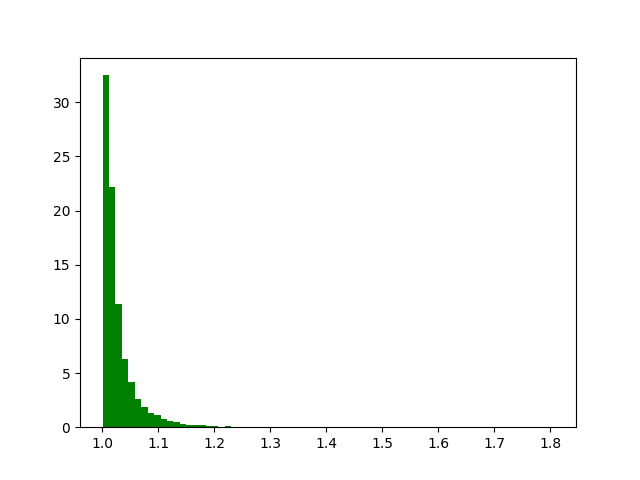
Generate confidence intervals for the DISTRIBUTION PARAMETERS with bootstrapping:

from scipy.stats import pareto

true_params = pareto.fit(data)
low_ci, up_ci = bootstrap_ci(data, pareto.fit, n_samples=1000)

low_ci[0] and up_ci[0] are the confidence intervals for the shape param

low_ci[0], true_params[0], up_ci[0] ---> (0.8786, 1.0983, 1.4599)

Ereshkigal

Answer 3

From the discussion on the other answer, I assume you want a confidence interval for the population mean, yes? (You have to have a confidence interval for some quantity, not the distribution itself.)

For all distributions with finite moments, the sampling distribution of the mean tends asymptotically to a normal distribution with mean equal to the population mean and variance equal to the population variance divided by n. So if you have a lot of data, $\mu \pm \Phi^{-1}(p) \sigma / \sqrt{n}$ should be a good approximation to the p-confidence interval of the population mean, even if the distribution is not normal.

Illailladvised

Answer 4

Current solution didn't work, because randint seems to be deprecated

np.random.seed(10)
point_estimates = []         # Make empty list to hold point estimates

for x in range(200):         # Generate 200 samples
    sample = np.random.choice(a= x, size=x.shape)
    point_estimates.append( sample.mean() )
sorted_estimates = np.sort(np.array(point_estimates))
conf_interval = [sorted_estimates[int(0.025 * N)], sorted_estimates[int(0.975 * N)]]
print(conf_interval, conf_interval[1] - conf_interval[0])
pd.DataFrame(point_estimates).plot(kind="density", legend= False)

Outsoar