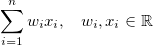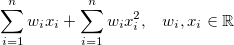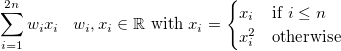Distinction between linear and non linear regression?

Question

In Machine Learning, we say that:

• w₁x₁ + w₂x₂ +...+ w_nx_n is a linear regression model where w₁,w₂....w_n are the weights and x₁,x₂...x₂ are the features whereas:
• w₁x₁² + w₂x₂² +...+ w_nx_n² is a non linear (polynomial) regression model

However, in some lectures I have seen people say a model is linear based on the weights, i.e. the coefficients of weights are linear and the degree of the features doesn't matter, whether they are linear(x₁) or polynomial(x₁²). Is that true? How does one differentiate a linear and non linear model? Is it based on weights or feature values?

Muslin

Answer 1

Both flavors exist.

If you are in the Statistics community it is usually former (nonlinearity in features, x^2 or e^x, etc). See this for example.

In the machine learning community the focus is more on the weights; the feature functions can be anything (see for example the kernel trick in SVMs).

The reason for this is that different communities have different approaches for solving these similar problems. The stat community has more of a direct and analytical approach; while the goal of machine learning is slightly different (modeling intricate complex patterns in an unknown concept space).

Lysenko

Thanks. In that case, when can weights be polynomial in nature? The weights are learnt through techniques like gradient descent right? So under what circumstances will they be linear or polynomial? – Muslin

Anything as long as they're differentiable can optimized via gradient descent (and it cousins). – Lysenko

Answer 2

How does one differentiate a linear and non linear model? Is it based on weights or feature values?

I've only heard / read about it in "a model is linear / nonlinear with respect to the features". This is usually the interesting thing. I don't see how having a term w_i² in your model will help you as it is essentially a constant. Only the features change during testing time.

So a linear model is something that can be expressed as

where the w_i define your model and the x_i are your input. Different w_i result in a different model (but they are all linear with respect to the features). If your model does not fit to that scheme, then your model is not linear with respect to the features.

Now, you can add new features which are essentially only (handcrafted) non-linear transformations of the input. For example, you could make a model

You could argue that this is a non-linear model with respect to the input. However, you can also argue that it is essentially the model

I think the important part here is that it was hand-crafted. You changed the feature space, not the abilities of the model. So it is still a linear model, but in another feature-space. When you go this way, you can make any model to be non-linear.

After all: Does it really matter? It sounds a bit like you're preparing for an exam. If this is the case, I suggest to just ask your lecturer and stick with what he defines as linear / non-linear.

Tristichous

Answer 3

Please join Stats SE and add to this discussion. I believe it is more appropriate in that context. However, to convince you to at least click the link, here is the SHORT ANSWER: "If (and only if) the statistical distribution of a model's noise (error) can be described using only linear combinations of observations, factors and/or predictors, that model is linear. Otherwise, it is not."

As you can see, I put a statistics spin on it because that is my educational background (actually more of applied mathematics with a recent heavy focus on probability). What this means is that when you subtract the prediction(s) of the model from the truth (vector), that equation must be expressible (sometimes through mathematical transformations) as a linear combination of the factors/predictors and the truth data as vectors in a linear space.

Extravagant

The equation to which I refer is error(s) = truth value(s) - predicted value(s). So all of the quantities must be in the same units; one cannot subtract apples from oranges or vice versa. If you transform the entire equation, that would work as long as the transformation is a linear one. – Extravagant