How to calculate minimum spanning tree in R

Question

Given a graph of N vertices and the distance between the edges of the vertices stored in tuple T1 = (d11, d12, …, d1n) to Tn = (dn1, dn2, …, dnn). Find out a minimum spanning tree of this graph starting from the vertex V1. Also, print the total distance travel needed to travel this generated tree.

Example:
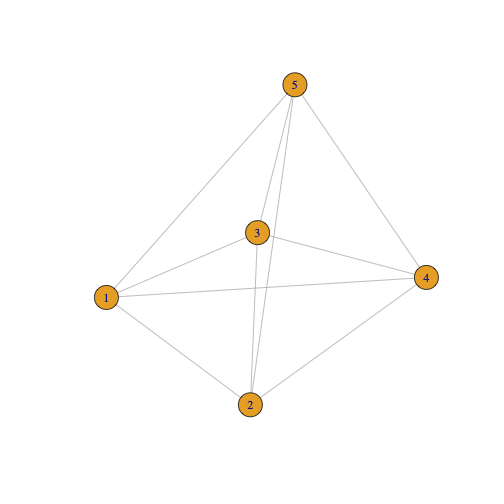
For N =5 
T1 = (0, 4, 5, 7, 5)
T2 = (4, 0, 6, 2, 5)
T3 = (5, 6, 0, 2, 1)
T4 = (7, 2, 2, 0, 5)
T5 = (5, 5, 1, 5, 0)

Selection of edges according to minimum distance are:
V1 -> V2 = 4
V2 -> V4 = 2
V4 -> V3 = 2
V3 -> V5 = 1

Thus, MST is V1 -> V2 -> V4 -> V3 -> V5 and the distance travelled is 9 (4+2+2+1)

Literally,I don't have idea about how to create a graph of n vertices in R.

I searched in google but i didn't understand how to approach above problem.

Please,help me.

Ninnette

did you check the igraph package, or this question or this function? – Sarena

Actually , I didn't have graph, Do i need to create a graph with n vertices? Little bit confused with the question – Ninnette

I think we can calculate minimum spanning tree if we have graph. How to get N vertices graph representing senario like in question? – Ninnette

convert your weights to an adjacent matrix: adj = rbind(T1, T2, T3, T4, T5) , then read into igraph : g = graph_from_adjacency_matrix(adj, weighted = TRUE) . Then you can calculate the mst – Middlebrooks

Those T1, T2,T3,T4,T5 are distances from vertices . How can i know those distances before .First , I have to create graph right? – Ninnette

on a second reading can you explain what "distance between the edges of the vertices" means please? Do you mean that it is the distance between the vertices i.e. length of edges / edge weights? – Middlebrooks

could you also explain what you mean in your comment above please "How can i know those distances before" as you question states that these distances are given. – Middlebrooks

Distance between the edges of the vertices means distance between the vertices. – Ninnette

When I tried your solution iam getting error like T1 <- c(0,4,5,7,5) > T2 = c(4, 0, 6, 2, 5) > T3 = c(5, 6, 0, 2, 1) > T4 = c(7, 2, 2, 0, 5) > T5 = c(5, 5, 1, 5, 0) > adj = rbind(T1, T2, T3, T4, T5) > g = graph_from_adjacency_matrix(adj, weighted = TRUE) > z<-mst(g, weights = TRUE) Error in mst(g, weights = TRUE) : At spanning_trees.c:287 : Invalid weights length, Invalid value – Ninnette

My doubt is for calculation of MST first we have to know graph of n vertices and second distances between the vertices right? Then only we can calculate MST. But above scenario is little bit confusing to me. I have posted full question i.e, they gave that much info to me. – Ninnette

I think you can just use mst(g) but perhaps also mst(g, weights = E(g)$weights) ? – Middlebrooks

"first we have to know graph of n vertices and second distances between the vertices right. Then only we can calculate MST. -- yes correct. If you have these things you can form the weighted graph, as we do in the code above. – Middlebrooks

can you see how adj above represents the code in your question and a weighted graph?. Each row/column gives the connection to the other nodes in the graph. If there was a zero in the adj matrix then there would be no edge. You often see these as unweighted adjacency matrices with only ones or zeros indicating an edge or not. As you are given weights (the distance between each edge) these are used in the adj matrix instead of ones to indicate the edge. – Middlebrooks

I got the output like this z IGRAPH f716a5f D-W- 5 4 -- + attr: weight (e/n) + edges from f716a5f: [1] 2->1 3->4 4->2 5->3 .Thank you. – Ninnette

I got MST. Also, I have to get distance travelled .How to get that output? – Ninnette

sum(E(mg)$weight), where mg is the minimum spanning tree graph – Middlebrooks

@user20650, Thank you . – Ninnette

you're welcome Magie – Middlebrooks

Answer 1

Your question doesn't seem to match the title - you're after the graph creation not the MST? Once you've got a graph, as @user20650 says, the MST itself is easy.

It is easy to create a graph of size n, but there is a whole lot of complexity about which nodes are connected and their weights (distances) that you don't tell us about, so this is a really basic illustration.

If we assume that all nodes are connected to all other nodes (full graph), we can use make_full_graph. If that isn't the case, you either need data to say which nodes are connected or use a random graph.

# create graph
n <- 5
g <- make_full_graph(n)

The next issue is the distances. You haven't given us any information on how those distances are distributed, but we can demonstrate assigning them to the graph. Here, I'll just use random uniform [0-1] numbers:

# number of edges in an (undirected) full graph is (n2 - n) /2 but
# it is easier to just ask the graph how many edges it has - this
# is more portable if you change from make_full_graph
n_edge <- gsize(g)
g <- set_edge_attr(g, 'weight', value=runif(n_edge))
plot(g)

The next bit is just the MST itself, using minimum.spanning.tree:

mst <-  minimum.spanning.tree(g)

The output mst looks like this:

IGRAPH dc21276 U-W- 5 4 -- Full graph
+ attr: name (g/c), loops (g/l), weight (e/n)
+ edges from dc21276:
[1] 1--4 1--5 2--3 2--5

Aeronautics

I too don't know about the how distances are calculated that's why i am confused. I have posted full question.They gave that much information only. And i am new to this MST topic. – Ninnette

We can't help with that. If you haven't been given information on the graph structure beyond n nodes, then it is only possible to give a generic answer with some assumptions. You could use random graphs and a different distribution of edge lengths and the code would still give the answer – Aeronautics

Yeah I know without graph and distances information it is difficult to help. With that info user20650 helped me. That is enough. – Ninnette

By the way your answer is useful for me because I came to know how to make a n graph in R. Thank you. – Ninnette