Why do we "pack" the sequences in PyTorch?

Question

I was trying to replicate How to use packing for variable-length sequence inputs for rnn but I guess I first need to understand why we need to "pack" the sequence.

I understand why we "pad" them but why is "packing" (via pack_padded_sequence) necessary?

Malmsey

all questions about packing in pytorch: discuss.pytorch.org/t/… – Gibb

Answer 1

I have stumbled upon this problem too and below is what I figured out.

When training RNN (LSTM or GRU or vanilla-RNN), it is difficult to batch the variable length sequences. For example: if the length of sequences in a size 8 batch is [4,6,8,5,4,3,7,8], you will pad all the sequences and that will result in 8 sequences of length 8. You would end up doing 64 computations (8x8), but you needed to do only 45 computations. Moreover, if you wanted to do something fancy like using a bidirectional-RNN, it would be harder to do batch computations just by padding and you might end up doing more computations than required.

Instead, PyTorch allows us to pack the sequence, internally packed sequence is a tuple of two lists. One contains the elements of sequences. Elements are interleaved by time steps (see example below) and other contains the size of each sequence the batch size at each step. This is helpful in recovering the actual sequences as well as telling RNN what is the batch size at each time step. This has been pointed by @Aerin. This can be passed to RNN and it will internally optimize the computations.

I might have been unclear at some points, so let me know and I can add more explanations.

Here's a code example:

 a = [torch.tensor([1,2,3]), torch.tensor([3,4])]
 b = torch.nn.utils.rnn.pad_sequence(a, batch_first=True)
 >>>>
 tensor([[ 1,  2,  3],
    [ 3,  4,  0]])
 torch.nn.utils.rnn.pack_padded_sequence(b, batch_first=True, lengths=[3,2])
 >>>>PackedSequence(data=tensor([ 1,  3,  2,  4,  3]), batch_sizes=tensor([ 2,  2,  1]))

Apoplectic

Can you explain why the output of the given example is PackedSequence(data=tensor([ 1, 3, 2, 4, 3]), batch_sizes=tensor([ 2, 2, 1])) ? – Cakewalk

Data part is just all the tensors concatenated along the time axis. Batch_size is actually the array of batch sizes at each time step. – Apoplectic

The batch_sizes=[2, 2, 1] represents grouping [1, 3] [2, 4] and [3] respectively. – Deck

@ChaitanyaShivade why is the batch size[2,2,1] ? can't it be [1,2,2]? what is the logic behind it? – Irreconcilable

Because at step t, you can only process vectors at step t, if you keep vectors ordered as [1,2,2], you are probably putting each input as a batch, but that can't be parallelized and hence not batchable – Apoplectic

I mostly understand this, but what still confuses me is that RNN expects input in the form [batch_size, seq, feature]. Am I correct that this means what we'll be padding+packing is seq? Which in your example is [1,2,3] and [3,4]? – Snowplow

@Snowplow From the pytorch docs (pytorch.org/docs/stable/generated/torch.nn.LSTM.html), The input can also be a packed variable length sequence. So you can convert the tensor of [batch_size, seq, feature] dim to a packed sequence and it will work. – Apoplectic

So does this mean that packing sequences is just for saving some computations (so speed/energy)? And identical training/learning would occur if otherwise done on just padded sequences with 0 imposed Loss at the pads? – Hombre

Yes, you are correct @ZaidGharaybeh. Packing is an engineering solution to save computations. It also makes using bi-directional RNN easier. For bi-RNN you will have to do padding twice (front and back of seq). – Apoplectic

Answer 2

Here are some visual explanations¹ that might help to develop better intuition for the functionality of pack_padded_sequence().

---

TL;DR: It is performed primarily to save compute. Consequently, the time required for training neural network models is also (drastically) reduced, especially when carried out on very large (a.k.a. web-scale) datasets.

---

Let's assume we have 6 sequences (of variable lengths) in total. You can also consider this number 6 as the batch_size hyperparameter. (The batch_size will vary depending on the length of the sequence (cf. Fig.2 below))

Now, we want to pass these sequences to some recurrent neural network architecture(s). To do so, we have to pad all of the sequences (typically with 0s) in our batch to the maximum sequence length in our batch (max(sequence_lengths)), which in the below figure is 9.

So, the data preparation work should be complete by now, right? Not really.. Because there is still one pressing problem, mainly in terms of how much compute do we have to do when compared to the actually required computations.

For the sake of understanding, let's also assume that we will matrix multiply the above padded_batch_of_sequences of shape (6, 9) with a weight matrix W of shape (9, 3).

Thus, we will have to perform 6x9 = 54 multiplication and 6x8 = 48 addition                     (nrows x (n-1)_cols) operations, only to throw away most of the computed results since they would be 0s (where we have pads). The actual required compute in this case is as follows:

 9-mult  8-add 
 8-mult  7-add 
 6-mult  5-add 
 4-mult  3-add 
 3-mult  2-add 
 2-mult  1-add
---------------
32-mult  26-add
   
------------------------------  
#savings: 22-mult & 22-add ops  
          (32-54)  (26-48) 

That's a LOT more savings even for this very simple (toy) example. You can now imagine how much compute (eventually: cost, energy, time, carbon emission etc.) can be saved using pack_padded_sequence() for large tensors with millions of entries, and million+ systems all over the world doing that, again and again.

The functionality of pack_padded_sequence() can be understood from the figure below, with the help of the used color-coding:

As a result of using pack_padded_sequence(), we will get a tuple of tensors containing (i) the flattened (along axis-1, in the above figure) sequences , (ii) the corresponding batch sizes, tensor([6,6,5,4,3,3,2,2,1]) for the above example.

The data tensor (i.e. the flattened sequences) could then be passed to objective functions such as CrossEntropy for loss calculations.

---

¹ image credits to @sgrvinod

Mireielle

Excellent diagrams! – Weighin

Edit: I think https://mcmap.net/q/135982/-why-do-we-quot-pack-quot-the-sequences-in-pytorch (below) answers my question, which I will leave here anyway: ~Does this essentially mean the gradients are not propagated to the padded inputs? What if my loss function is only computed on the final hidden state/output of the RNN? Must the efficiency gains be thrown away then? Or will the loss be computed from the step before where the padding starts, which is different for each batch element in this example?~ – Altocumulus

I was intrigued with how exactly the matrix multiplication is done, since the RNN feeding should be sequential, taking only a part of the packed vector at once. The full explanation is given in this great tutorial: github.com/sgrvinod/a-PyTorch-Tutorial-to-Sequence-Labeling – Unsought

This was an excellent visualization. Based on what you have presented, I now wonder why we even need padding. It seems as part of packing we get rid of pads. So why do we even add them to begin with? – Barton

Answer 3

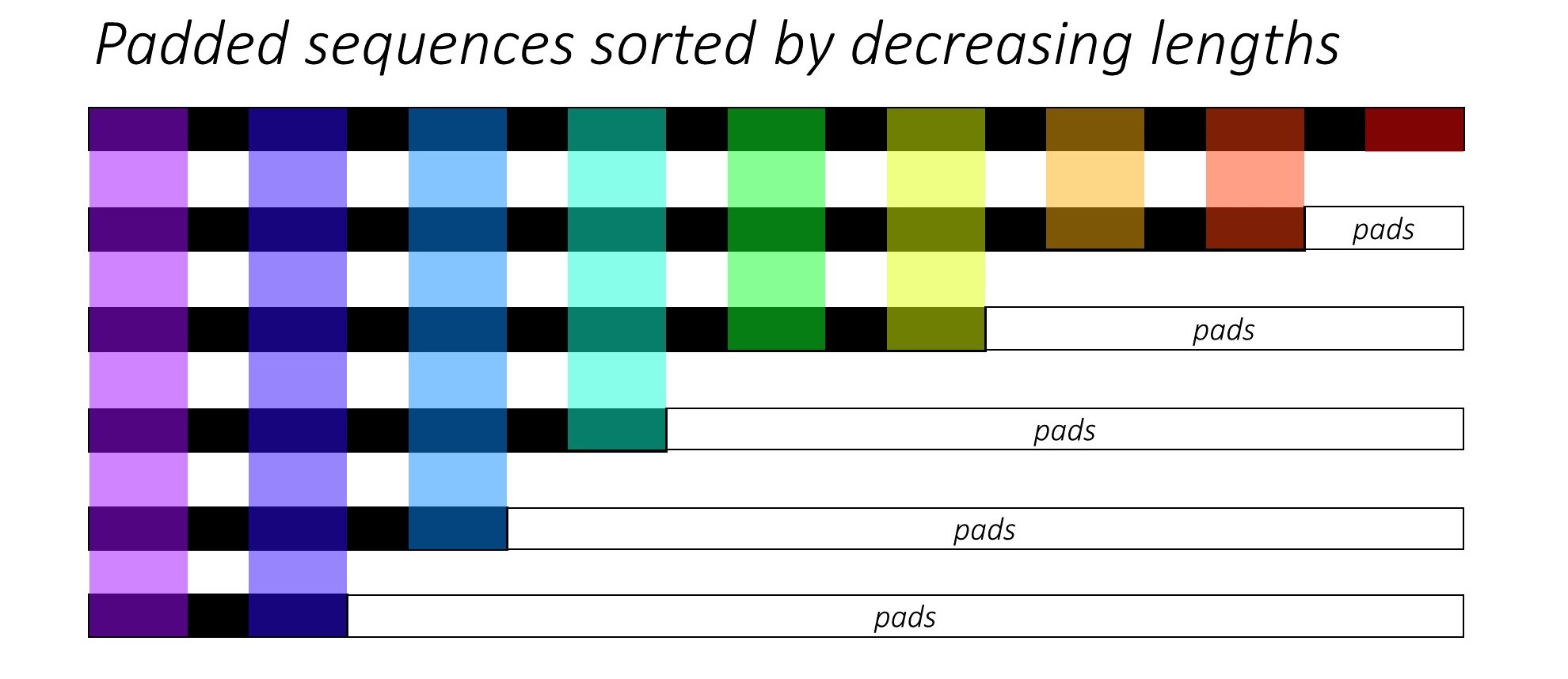
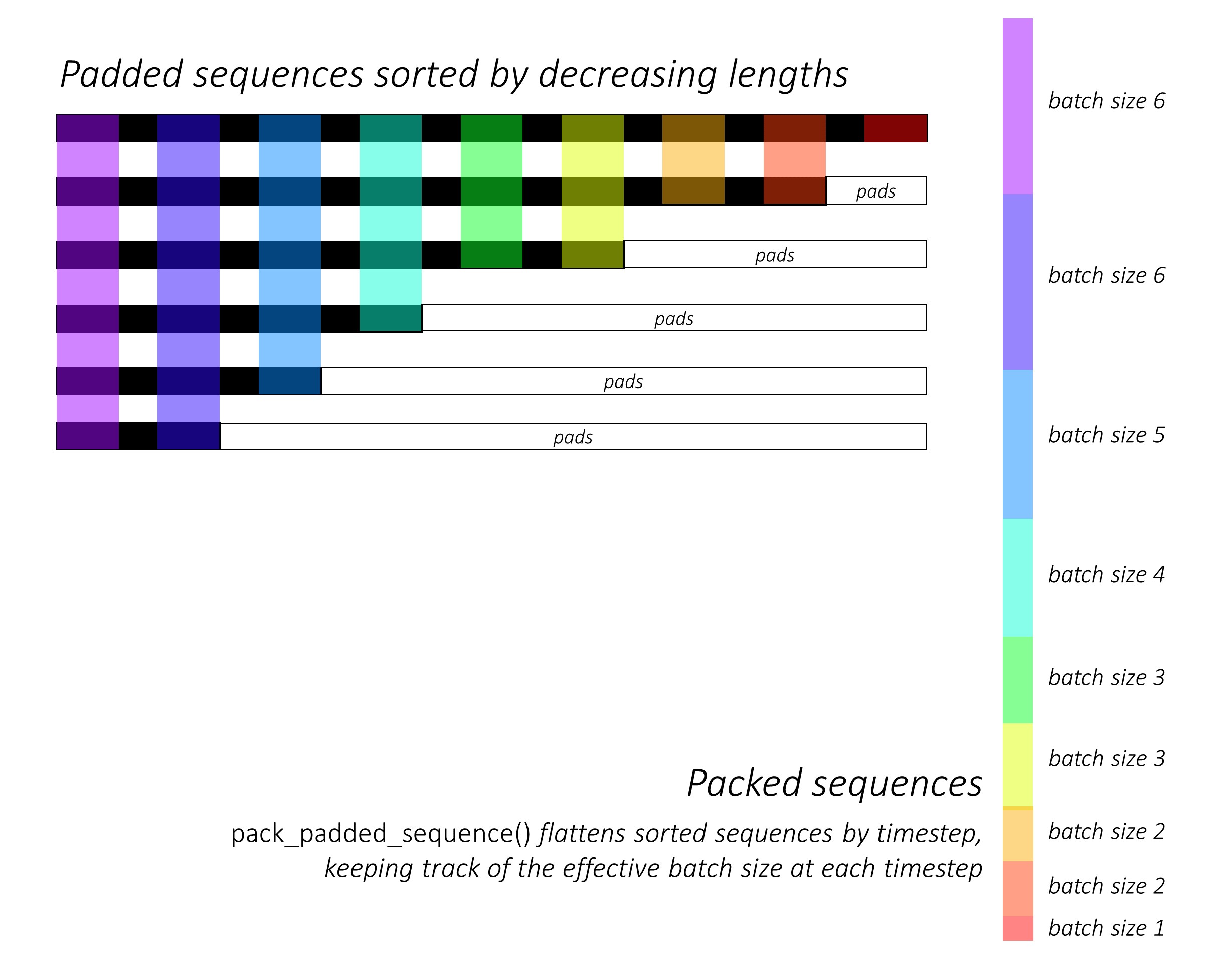
The above answers addressed the question why very well. I just want to add an example for better understanding the use of pack_padded_sequence.

Let's take an example

Note: pack_padded_sequence requires sorted sequences in the batch (in the descending order of sequence lengths). In the below example, the sequence batch were already sorted for less cluttering. Visit this gist link for the full implementation.

First, we create a batch of 2 sequences of different sequence lengths as below. We have 7 elements in the batch totally.

• Each sequence has embedding size of 2.
• The first sequence has the length: 5
• The second sequence has the length: 2

import torch 

seq_batch = [torch.tensor([[1, 1],
                           [2, 2],
                           [3, 3],
                           [4, 4],
                           [5, 5]]),
             torch.tensor([[10, 10],
                           [20, 20]])]

seq_lens = [5, 2]

We pad seq_batch to get the batch of sequences with equal length of 5 (The max length in the batch). Now, the new batch has 10 elements totally.

# pad the seq_batch
padded_seq_batch = torch.nn.utils.rnn.pad_sequence(seq_batch, batch_first=True)
"""
>>>padded_seq_batch
tensor([[[ 1,  1],
         [ 2,  2],
         [ 3,  3],
         [ 4,  4],
         [ 5,  5]],

        [[10, 10],
         [20, 20],
         [ 0,  0],
         [ 0,  0],
         [ 0,  0]]])
"""

Then, we pack the padded_seq_batch. It returns a tuple of two tensors:

• The first is the data including all the elements in the sequence batch.
• The second is the batch_sizes which will tell how the elements related to each other by the steps.

# pack the padded_seq_batch
packed_seq_batch = torch.nn.utils.rnn.pack_padded_sequence(padded_seq_batch, lengths=seq_lens, batch_first=True)
"""
>>> packed_seq_batch
PackedSequence(
   data=tensor([[ 1,  1],
                [10, 10],
                [ 2,  2],
                [20, 20],
                [ 3,  3],
                [ 4,  4],
                [ 5,  5]]), 
   batch_sizes=tensor([2, 2, 1, 1, 1]))
"""

Now, we pass the tuple packed_seq_batch to the recurrent modules in Pytorch, such as RNN, LSTM. This only requires 5 + 2=7 computations in the recurrrent module.

lstm = nn.LSTM(input_size=2, hidden_size=3, batch_first=True)
output, (hn, cn) = lstm(packed_seq_batch.float()) # pass float tensor instead long tensor.
"""
>>> output # PackedSequence
PackedSequence(data=tensor(
        [[-3.6256e-02,  1.5403e-01,  1.6556e-02],
         [-6.3486e-05,  4.0227e-03,  1.2513e-01],
         [-5.3134e-02,  1.6058e-01,  2.0192e-01],
         [-4.3123e-05,  2.3017e-05,  1.4112e-01],
         [-5.9372e-02,  1.0934e-01,  4.1991e-01],
         [-6.0768e-02,  7.0689e-02,  5.9374e-01],
         [-6.0125e-02,  4.6476e-02,  7.1243e-01]], grad_fn=<CatBackward>), batch_sizes=tensor([2, 2, 1, 1, 1]))

>>>hn
tensor([[[-6.0125e-02,  4.6476e-02,  7.1243e-01],
         [-4.3123e-05,  2.3017e-05,  1.4112e-01]]], grad_fn=<StackBackward>),
>>>cn
tensor([[[-1.8826e-01,  5.8109e-02,  1.2209e+00],
         [-2.2475e-04,  2.3041e-05,  1.4254e-01]]], grad_fn=<StackBackward>)))
"""

We need to convert output back to the padded batch of output:

padded_output, output_lens = torch.nn.utils.rnn.pad_packed_sequence(output, batch_first=True, total_length=5)
"""
>>> padded_output
tensor([[[-3.6256e-02,  1.5403e-01,  1.6556e-02],
         [-5.3134e-02,  1.6058e-01,  2.0192e-01],
         [-5.9372e-02,  1.0934e-01,  4.1991e-01],
         [-6.0768e-02,  7.0689e-02,  5.9374e-01],
         [-6.0125e-02,  4.6476e-02,  7.1243e-01]],

        [[-6.3486e-05,  4.0227e-03,  1.2513e-01],
         [-4.3123e-05,  2.3017e-05,  1.4112e-01],
         [ 0.0000e+00,  0.0000e+00,  0.0000e+00],
         [ 0.0000e+00,  0.0000e+00,  0.0000e+00],
         [ 0.0000e+00,  0.0000e+00,  0.0000e+00]]],
       grad_fn=<TransposeBackward0>)

>>> output_lens
tensor([5, 2])
"""

Compare this effort with the standard way

1. In the standard way, we only need to pass the padded_seq_batch to lstm module. However, it requires 10 computations. It involves several computes more on padding elements which would be computationally inefficient.

2. Note that it does not lead to inaccurate representations, but need much more logic to extract correct representations.

   • For LSTM (or any recurrent modules) with only forward direction, if we would like to extract the hidden vector of the last step as a representation for a sequence, we would have to pick up hidden vectors from T(th) step, where T is the length of the input. Picking up the last representation will be incorrect. Note that T will be different for different inputs in batch.
   • For Bi-directional LSTM (or any recurrent modules), it is even more cumbersome, as one would have to maintain two RNN modules, one that works with padding at the beginning of the input and one with padding at end of the input, and finally extracting and concatenating the hidden vectors as explained above.

Let's see the difference:

# The standard approach: using padding batch for recurrent modules
output, (hn, cn) = lstm(padded_seq_batch.float())
"""
>>> output
 tensor([[[-3.6256e-02, 1.5403e-01, 1.6556e-02],
          [-5.3134e-02, 1.6058e-01, 2.0192e-01],
          [-5.9372e-02, 1.0934e-01, 4.1991e-01],
          [-6.0768e-02, 7.0689e-02, 5.9374e-01],
          [-6.0125e-02, 4.6476e-02, 7.1243e-01]],

         [[-6.3486e-05, 4.0227e-03, 1.2513e-01],
          [-4.3123e-05, 2.3017e-05, 1.4112e-01],
          [-4.1217e-02, 1.0726e-01, -1.2697e-01],
          [-7.7770e-02, 1.5477e-01, -2.2911e-01],
          [-9.9957e-02, 1.7440e-01, -2.7972e-01]]],
        grad_fn= < TransposeBackward0 >)

>>> hn
tensor([[[-0.0601, 0.0465, 0.7124],
         [-0.1000, 0.1744, -0.2797]]], grad_fn= < StackBackward >),

>>> cn
tensor([[[-0.1883, 0.0581, 1.2209],
         [-0.2531, 0.3600, -0.4141]]], grad_fn= < StackBackward >))
"""

The above results show that hn, cn are different in two ways while output from two ways lead to different values for padding elements.

Clotilde

Nice answer! Just a correction if you do padding you should not use the last h rather h at the index equal to length of input. Also, to do bidirectional RNN you would want to use two different RNN --- one with padding in the front and another with padding at the back to get correct results. Padding and picking last output is "wrong". So your arguments that it leads to inaccurate representation is wrong. The problem with padding is it is correct but inefficient (if packed sequences option is there) and can be cumbersome (for example: bi-dir RNN) – Apoplectic

I'm trying to understand how Note that it does not lead to inaccurate representations is a true statement. I think the argument is that passing 0's through the RNN wouldn't change the output but it seems like this would be true only if the biases were all equal to 0 – Meagan

Usually, an embedding layer is required for LSTMs. Would we be passing it into embedding layer in the same format and then into LSTM layer? – Sculpsit

Answer 4

Adding to Umang's answer, I found this important to note.

The first item in the returned tuple of pack_padded_sequence is a data (tensor) -- a tensor containing the packed sequence. The second item is a tensor of integers holding information about the batch size at each sequence step.

What's important here though is the second item (Batch sizes) represents the number of elements at each sequence step in the batch, not the varying sequence lengths passed to pack_padded_sequence.

For instance, given the data abc and x the :class:PackedSequence would contain the data axbc with batch_sizes=[2,1,1].

Malmsey

Thanks, I totally forgot that. and made a mistake in my answer going to update that. However, I looked at the second sequence as some data required to recover the sequences and that is why messed up my description – Apoplectic

Answer 5

I used pack padded sequence as follows.

packed_embedded = nn.utils.rnn.pack_padded_sequence(seq, text_lengths)
packed_output, hidden = self.rnn(packed_embedded)

where text_lengths are the length of the individual sequence before padding and sequence are sorted according to decreasing order of length within a given batch.

you can check out an example here.

And we do packing so that the RNN doesn't see the unwanted padded index while processing the sequence which would affect the overall performance.

Piecework