R Two graphs with lines going from one to the other

Question

I want to plot some point in a normal graph and link those points to a map displayed under it. What I would like to have basically is that (here I added manually the links):

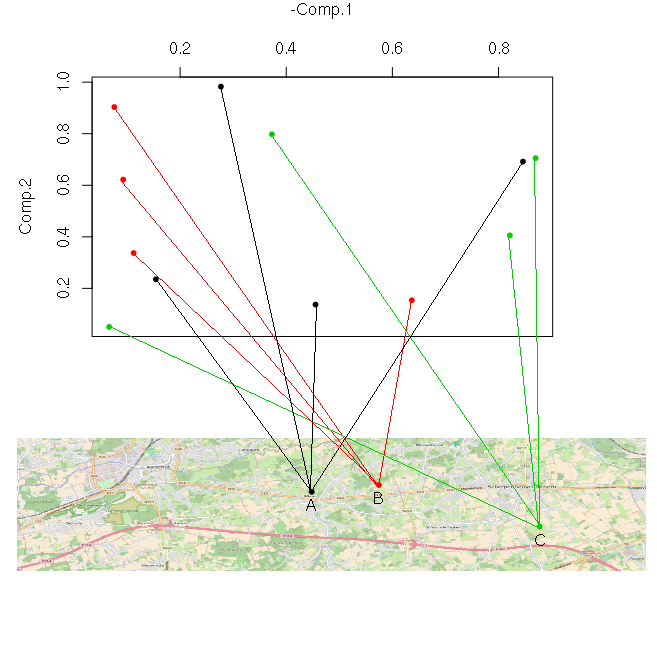
Somehow I should use segments with pdt=T to write outside the margins, but I am not sure what mathematical transformation I need to do in order to set the right coordinates for the segment extremity that go into the map.

And I would prefere to use the traditional plot function and not ggplot2

Here the source used to draw the exemple (warning it may take time to load the open street map):

library(OpenStreetMap)
#Random point to plot in the graph
fdata=cbind.data.frame(runif(12),runif(12),c(rep("A",4),rep("B",4),rep("C",4)))
colnames(fdata)=c("x","y","city")

#random coordinate to plot in the map
cities=cbind.data.frame(runif(3,4.8,5),runif(3,50.95,51),c("A","B","C"))
colnames(cities)=c("long","lat","name")

#city to color correspondance
color=1:length(cities$name)
names(color)=cities$name


maxlat=max(cities$lat)
maxlong=max(cities$long)
minlat=min(cities$lat)
minlong=min(cities$long)

#get some open street map
map = openmap(c(lat=maxlat+0.02,long=minlong-0.04 ) ,
              c(lat=minlat-0.02,long=maxlong+.04) ,
              minNumTiles=9,type="osm")
longlat=openproj(map) #Change coordinate projection


par(mfrow=c(2,1),mar=c(0,5,4,6))

plot( fdata$y ~ fdata$x ,xaxt="n",ylab="Comp.2",xlab="",col=color[fdata$city],pch=20)
axis(3)
mtext(side=3,"-Comp.1",line=3)
par(mar=rep(1,4))

#plot the map
plot(longlat,removeMargin=F)
points(cities$lat ~ cities$long, col= color[cities$name],cex=1,pch=20)
text(cities$long,cities$lat-0.005,labels=cities$name)

Com

Answer 1

The grid graphical system (which underlies both the lattice and ggplot2 graphics packages) is much better suited to this sort of operation than is R's base graphical system. Unfortunately, both of your plots use the base graphical system. Fortunately, though, the superb gridBase package supplies functions that allow one to translate between the two systems.

In the following (which starts with your call to par(mfrow=c(2,1),...)), I've marked the lines I added with comments indicating that they are My addition. For another, somewhat simpler example of this strategy in action, see here.

library(grid)      ## <-- My addition
library(gridBase)  ## <-- My addition

par(mfrow=c(2,1),mar=c(0,5,4,6))
plot(fdata$y ~ fdata$x, xaxt = "n", ylab = "Comp.2", xlab = "",
     col = color[fdata$city],pch=20)
vps1 <- do.call(vpStack, baseViewports()) ## <-- My addition
axis(3)
mtext(side = 3,"-Comp.1",line=3)
par(mar = rep(1,4))

#plot the map
plot(longlat,removeMargin=F)
vps2 <- do.call(vpStack, baseViewports()) ## <-- My addition
points(cities$lat ~ cities$long, col= color[cities$name],cex=1,pch=20)
text(cities$long,cities$lat-0.005,labels=cities$name)

## My addition from here on out...    

## A function that draws a line segment between two points (each a
## length two vector of x-y coordinates), the first point in the top
## plot and the second in the bottom plot.
drawBetween <- function(ptA, ptB, gp = gpar()) {
    ## Find coordinates of ptA in "Normalized Parent Coordinates"
    pushViewport(vps1)
    X1 <- convertX(unit(ptA[1],"native"), "npc")
    Y1 <- convertY(unit(ptA[2],"native"), "npc")
    popViewport(3)
    ## Find coordinates of ptB in "Normalized Parent Coordinates"
    pushViewport(vps2)
    X2 <- convertX(unit(ptB[1],"native"), "npc")
    Y2 <- convertY(unit(ptB[2],"native"), "npc")
    popViewport(3)
    ## Plot line between the two points
    grid.move.to(x = X1, y = Y1, vp = vps1)
    grid.line.to(x = X2, y = Y2, vp = vps2, gp = gp)
}

## Try the function out on one pair of points
ptA <- fdata[1, c("x", "y")]
ptB <- cities[1, c("long", "lat")]
drawBetween(ptA, ptB, gp = gpar(col = "gold"))

## Using a loop, draw lines from each point in `fdata` to its
## corresponding city in `cities`
for(i in seq_len(nrow(fdata))) {
    ptA <- fdata[i, c("x", "y")]
    ptB <- cities[match(fdata[i,"city"], cities$name), c("long", "lat")]
    drawBetween(ptA, ptB, gp = gpar(col = color[fdata[i,"city"]]))
}

Oligarch

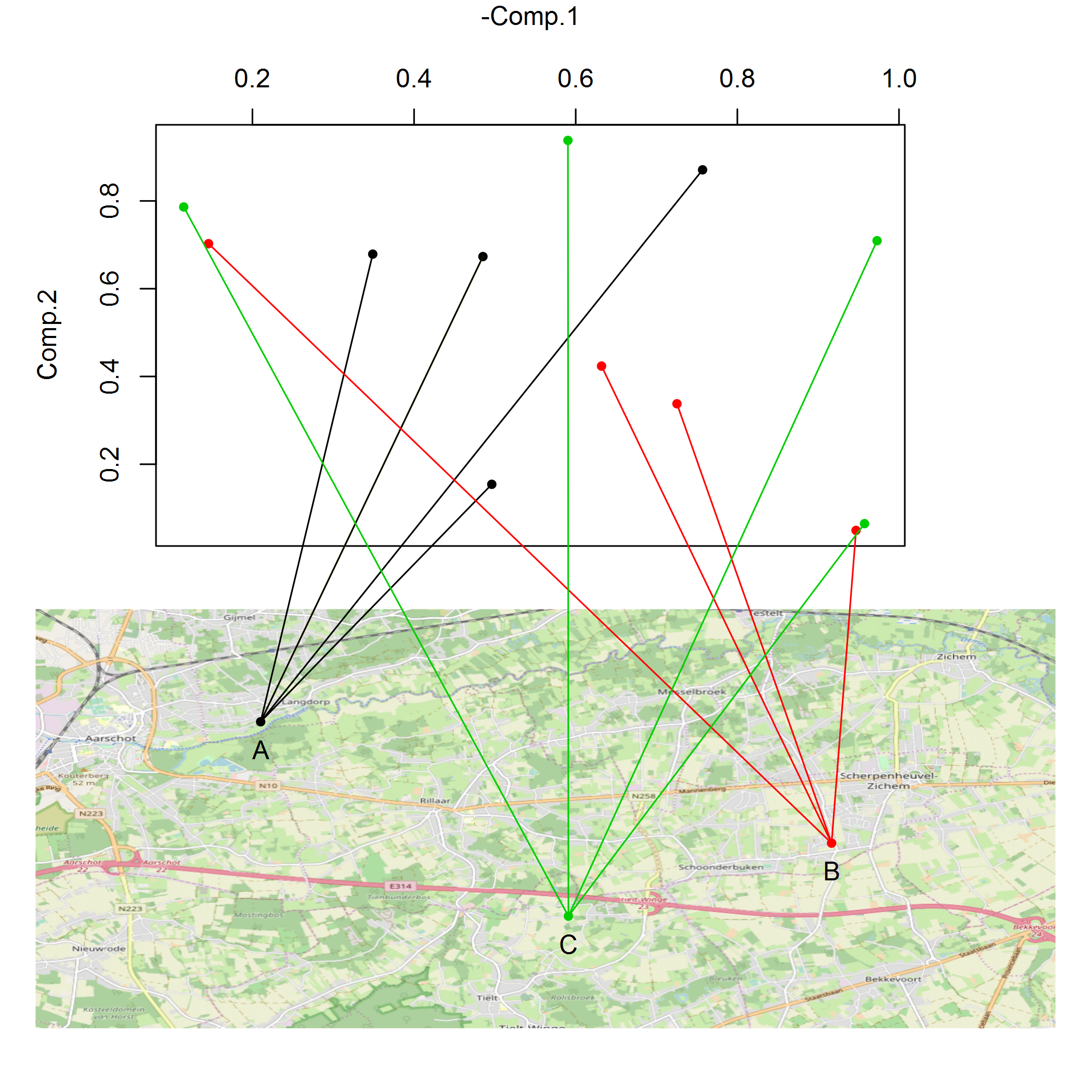
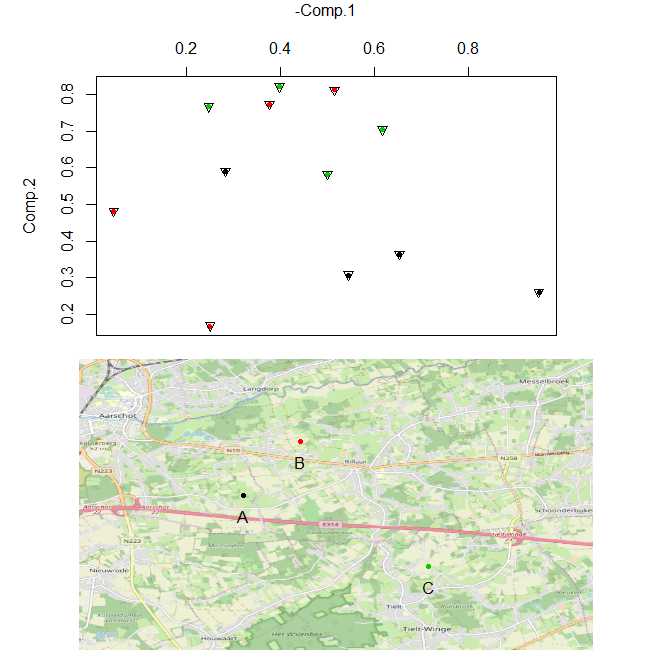
That works like a charm! I don't use ggplot nor lattice by choice, and prefere going as full "base-R" as possible. I'll wait a few more days before accepting the answer and award the bounty! thank you very much. – Com

Answer 2

You can create a new plot area over your plots and then add the lines:

#New plot area
par(new=T, mfrow = c(1,1))
plot(0:1, type = "n", xaxt='n', ann=FALSE,  axes=FALSE, frame.plot=TRUE, bty="n")

The problem of this is that you need do the mapping between yours plot and the new plot area, if you ever use the same area you can get some references (see locator) and then interpolate all the other point.

For example, in mi plot B is {1.751671, 0.1046729} and 8th point is {1.320507, 0.6892523}:

points(c(1.320507, 1.751671), c(0.6892523, 0.1046729), col = "red", type = "l")

UPDATE (Plots mapping):

X11(7, 7)

par(mfrow=c(2,1),mar=c(0,5,4,6))
plot( fdata$y ~ fdata$x ,xaxt="n",ylab="Comp.2",xlab="",col=color[fdata$city],pch=20)
axis(3)
mtext(side=3,"-Comp.1",line=3)
usr1 <- par("usr")

#plot the map
par(mar=rep(1,4))
plot(longlat,removeMargin=F)
points(cities$lat ~ cities$long, col= color[cities$name],cex=1,pch=20)
text(cities$long,cities$lat-0.005,labels=cities$name)
usr2 <- par("usr")


par(new=T, mfrow = c(1,1))
plot(0:1, type = "n", xaxt='n', ann=FALSE,  axes=FALSE, frame.plot=TRUE, bty="n")

# Position of the corners (0, 0) and (1, 1) of the two graphs in the window X11(7, 7)
#ref <- locator()
ref <- list(x = c(1.09261365729382, 1.8750001444129, 1.06363637999312, 1.93636379046146), 
            y = c(0.501704460496285, 0.941477257177598, 
                  -0.0335228967050026, 0.45909081740701))

fdata$x_map <- approxfun(usr1[1:2], ref$x[1:2])(fdata$x)
fdata$y_map <- approxfun(usr1[3:4], ref$y[1:2])(fdata$y)

points(fdata$y_map ~ fdata$x_map ,pch=6)

Keep in mind that the interpolation of the map must consider the projection, the linear projection can only be used with UTM coordinates.

Escalera

thanks for your answer, so what you propose is to manually (using locator) find the position of the 0s of two underlying dimensions to be able to locate them in a third dimension and then be able to convert coordinates from one dimension to the other. Sounds like a not so bad alternative but sounds strange that it is not possible to know exactly where the plot are within the general dev... Maybe using layout insted of par(mar=c(2,1))... If I have time i will investigate that more in details. – Com

Yes, that's it. And if you fix the dimension of the graphic window you can automate it by taking the positions of the corners (0, 0) and (1, 1) of the graphs only once and the pair ("usr") of each one (keep in mind that the interpolation of the map must consider the projection). I update the answer with a small example. – Margalit