How to extract the BSpline basis from scipy.interpolate.BSpline

Question

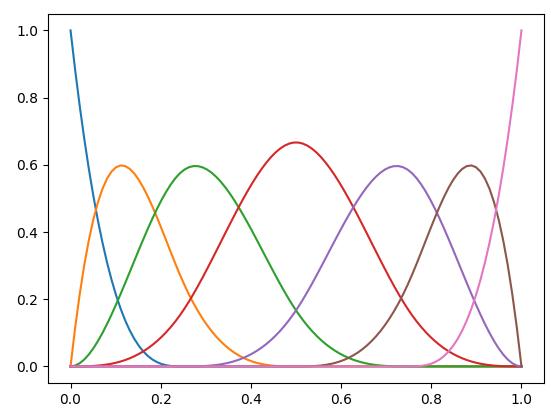
In this question I asked the community about how scipy.interpolate.splev calculates a spline basis.. My goal was to compute a spline faster then splev by pre-calculating a bspline basis and generate a curve by doing a basis to control point dot product.

Since then a new scipy.interpolate.BSpline interpolator was added to scipy. It comes with a basis_element function, which I presume could be used to return the basis used to calculate a spline.

So for example using the code from here with the inputs below:

import numpy as np

# Control points
cv = np.array([[ 50.,  25., 0.],
       [ 59.,  12., 0.],
       [ 50.,  10., 0.],
       [ 57.,   2., 0.],
       [ 40.,   4., 0.],
       [ 40.,   14., 0.]])

kv = [0, 0, 0, 0, 1, 2, 3, 3, 3, 3] # knot vector
n = 10  # 10 samples (keeping it simple)
degree = 3 # Curve degree

I can compute the following bspline basis:

[[ 1.          0.          0.          0.          0.          0.        ]
 [ 0.2962963   0.56481481  0.13271605  0.00617284  0.          0.        ]
 [ 0.03703704  0.51851852  0.39506173  0.04938272  0.          0.        ]
 [ 0.          0.25        0.58333333  0.16666667  0.          0.        ]
 [ 0.          0.07407407  0.54938272  0.36728395  0.00925926  0.        ]
 [ 0.          0.00925926  0.36728395  0.54938272  0.07407407  0.        ]
 [ 0.          0.          0.16666667  0.58333333  0.25        0.        ]
 [ 0.          0.          0.04938272  0.39506173  0.51851852  0.03703704]
 [ 0.          0.          0.00617284  0.13271605  0.56481481  0.2962963 ]
 [ 0.          0.          0.          0.          0.          1.        ]]

Using np.dot with basis and control points returns 10 samples on curve:

[[ 50.          25.           0.        ]
 [ 55.12654321  15.52469136   0.        ]
 [ 55.01234568  11.19753086   0.        ]
 [ 53.41666667   9.16666667   0.        ]
 [ 53.14506173   7.15432099   0.        ]
 [ 53.1882716    5.17901235   0.        ]
 [ 51.58333333   3.83333333   0.        ]
 [ 47.20987654   3.87654321   0.        ]
 [ 42.31790123   6.7345679    0.        ]
 [ 40.          14.           0.        ]]

Question : is it possible to extract the basis as described above out of scipy.interpolate.BSpline?

Obviously I must be using it wrong, because when I try I get something like this:

from scipy.interpolate import BSpline
b = BSpline.basis_element(kv)
print b(np.linspace(kv[0],kv[-1],n)) # i'm not sure what these values represent
[ 0.          0.00256299  0.04495618  0.16555213  0.28691315  0.28691315
  0.16555213  0.04495618  0.00256299  0.        ]

Krissy

Answer 1

BSpline.basis_element takes as its arguments the internal knots.

In your example, you padded the knots, and that did not do what you thought it would:

In [3]: t = [0, 0, 0, 0, 1, 2, 3, 3, 3, 3]

In [4]: b = BSpline.basis_element(t)

In [5]: b.k
Out[5]: 8

So it's an 8th order spline.

If you wanted a quadratic spline, you would do

In [7]: b1 = BSpline.basis_element([0, 1, 2, 3])

In [8]: b1.k
Out[8]: 2

In [9]: b1.t
Out[9]: array([-1., -1.,  0.,  1.,  2.,  3.,  4.,  4.])

Confused? The method is quite simple: https://github.com/scipy/scipy/blob/v0.19.1/scipy/interpolate/_bsplines.py#L243-L302

The callable returned by BSpline.basis_element is really a b-spline function. The result of calling it with an array argument is then equivalent to directly running the example code in the BSpline docstring in a loop for each element of your array, https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.BSpline.html

EDIT: if you're after a variant of Cox-de Boor algorithm of calculating all non-zero splines at a given point, then you can look at a _bspl.evaluate_all_bsplines function, https://github.com/scipy/scipy/blob/v0.19.1/scipy/interpolate/_bspl.pyx#L161 (which itself is just a wrapper over a C routine which does all the heavy lifting; note that it's hard to beat that latter one performance wise.)

However, it's not a public function, so it's not guaranteed to be available in future versions. If you have a good use for it, and a suggestion for a user-facing API, bring the discussion over to the scipy bug tracker.

Cassel

Thanks for clarifying. I got confused by terminology. – Krissy

Answer 2

To extract the basis functions from scipy.interpolate.BSpline, you just need to call it with unit coefficients, such as [1,0,0], [0,1,0], [0,0,1]. For example:

import numpy as np
import scipy.interpolate as intrp
import matplotlib.pyplot as plt

these_knots = np.linspace(0,1,5)
numpyknots = np.concatenate(([0,0,0],these_knots,[1,1,1])) 

n = len(these_knots)+2
basis = [0,]*n
for i in range(n):
    coef = (np.arange(n)==i).astype(float)
    print(coef)
    basis[i] = intrp.BSpline(numpyknots, coef, 3)

x = np.linspace(0., 1., 100)
for i in range(n):
   plt.plot(x,basis[i](x))

plt.show()

see this post

Grendel