Numerical issues integrating a pulse signal that is delayed (fixedDelay)

Question

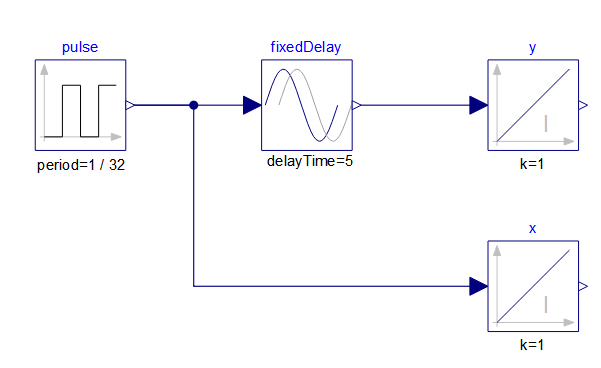
I noted numerical issues integrating a pulse input that is delayed by a fixed amount of time in Modelica (using Wolfram System Modeler 4.3):

model PulseTest "Test FixedDelay with Pulse Input";
    Modelica.Blocks.Sources.Pulse pulse(
        startTime = 1, 
        width = 100, 
        period = 1/32, 
        amplitude = 32, 
        nperiod = 1
    );
    Modelica.Blocks.Nonlinear.FixedDelay fixedDelay( delayTime = 5 );
    Modelica.Blocks.Continuous.Integrator x; // integrator for the undelayed pulse
    Modelica.Blocks.Continuous.Integrator y; // integrator for the delayed pulse
equation
    connect( pulse.y, fixedDelay.u );
    connect( fixedDelay.y, y.u );
    connect( pulse.y, x.u );
end PulseTest;

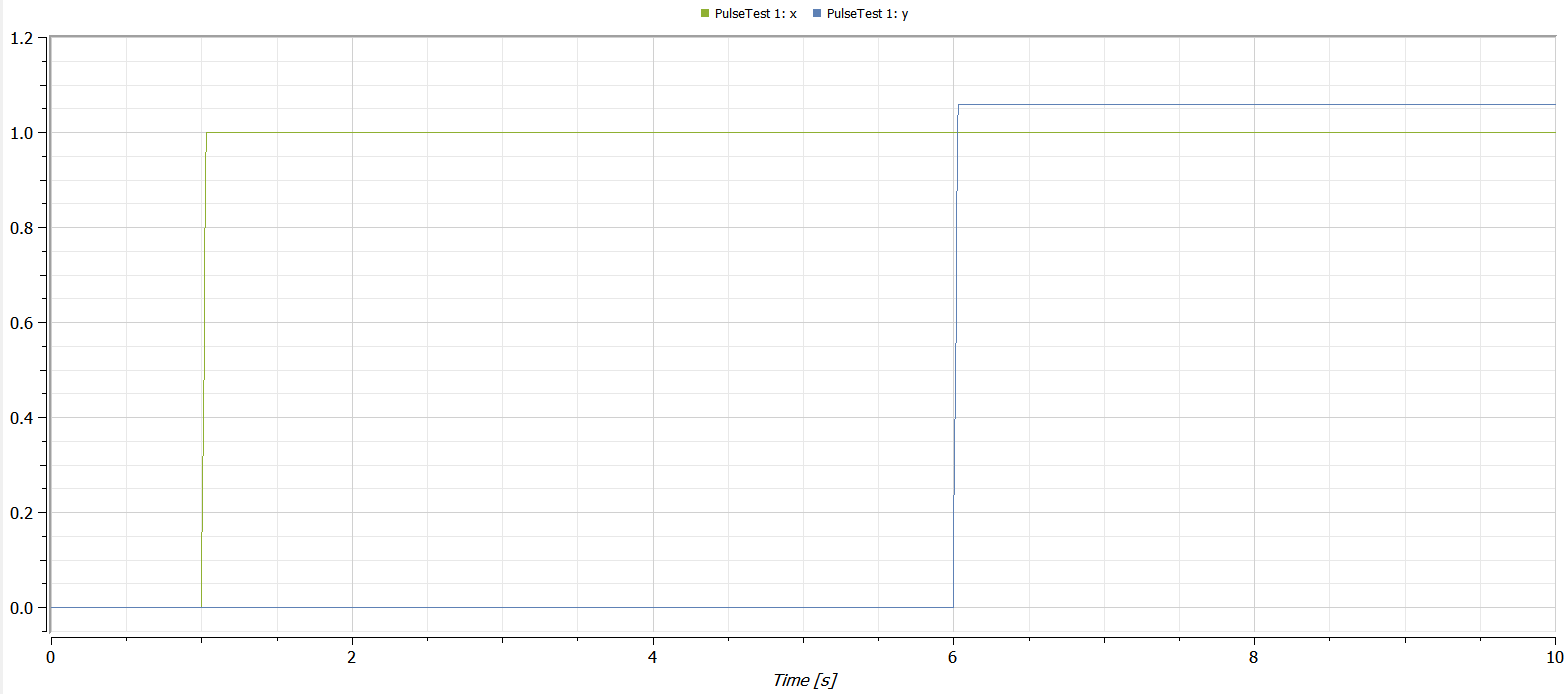
Integrating a pulse with period = 1/a, amplitude = a, and width = 100 % should give 1.0. But as can be seen from the plot, this is not what I get for the delayed pulse:

Only the undelayed signal gives the correct value using DASSL. The numerical integration error will appear already for period = 1/a = 1/8 and (naturally) grow as a grows.

What is the best remedy?

Dellinger

Throwing this in Dymola yields the same result. So not a systemmodeler issue. Changing the number of "steps" in the solver changes the solution with n->infinity providing the correct answer. Just an FYI and by itself not immensely useful – Playwright

@ScottG Thanks for the information. I sure hope there is something else that can be done; the way DASSL handles the fixed delay takes a lot of "joy" out of using Modelica for my purposes. – Dellinger

I've stumbled upon this behavior before but with a different application whose approach I don't think is amenable to what you are trying. But the gist for that was that I needed the code to generate an event at the appropriate times to ensure that it didn't spread out the signal. My first thoughts with your problem was to use a when statement in a fancy way and essentially create your own delay model. We'll see if someone else responds with good solution in the meantime. – Playwright

I did a quick review of the problem in Dymola and can confirm that it exists there as well. It seems like the original pulse is described well with events, but the one coming out of the delay is not a correct pulse anymore. How close it comes to the pulse depends on the solver stepsize, which in turn seems to be influenced by the number of steps as Scott describes. – Majors

Another thing that popped up during my tests is that choosing a fixed step solver seems to cause the second pulse to completely disappear from the result - which is even more worrisome than the original problem with imprecise integration. – Majors

@MarkusA. It all depends: Fixed step Euler (stepsize 0.001) will get correct pulse and integral, but Runge Kutta and, I believe Heun’s method, will not - here the pulse will indeed disappear. It is far from “easy going” unfortunately. – Dellinger

@gwr: Again a confirmation, Fixed step Euler works with 1ms step size in Dymola. I tried a step size of 5e-5 to cover the period time of 1/32. This makes the delayed pulse disappear. – Majors

I tried it in OpenModelica, and also see a similar result (although the value is too small instead of to large (0.8 instead of 1.1 that you show) – Revile

FYI: Works well in SimulationX with all available solvers. – Hound

Answer 1

As Ankit posted at the Wolfram Forum, the problem is that the signal is discrete but the delay block is unaware of that. It can be fixed with a different delay block:

model DiscreteFixedDelay
  discrete input Modelica.Blocks.Interfaces.RealInput u ;
  discrete output Modelica.Blocks.Interfaces.RealOutput y ;
  parameter Modelica.SIunits.Time delayTime(start = 5) = 5 "Delay time of output with respect to input signal";
equation
  y = delay(u, delayTime);
end DiscreteFixedDelay;

Regards

Aloud

Unfortunately, that solution leads to more special models that separate discrete from continuous components losing on generality. Note, that even the "discrete" pulse output is not modeled as discrete. Too bad, there is no better way to handle this. – Dellinger

Answer 2

The problem is, as Markus A wrote, that that delay does not propagate the discontinuity from input to output and therefore the simulation does not handle the delayed step-change in the same way as a normal step-change, i.e. with event-detection and event-handling.

From a tool-perspective smoothly interpolation the delayed signal is not merely the simplest solution - but also avoids a cascade of events if the delayed signal is fed back.

I cannot see any simple reliable workaround when using any variable step-size solver.

Acetabulum

Thank you (+1), unfortunately that is very sobering news. The comment by tbeu above suggests that the solver in SimulationX approaches the problem more intelligently? Obviously, there should be a better way to propagate discontinuities in a fixedDelay? (At least, using Euler and fixed steps for example gave me a lot of other problems in my models...) – Dellinger

I would say it is a different trade-off; the problem with propagating discontinuities is that you might get a cascade of propagated discontinuities causing other problems. – Acetabulum