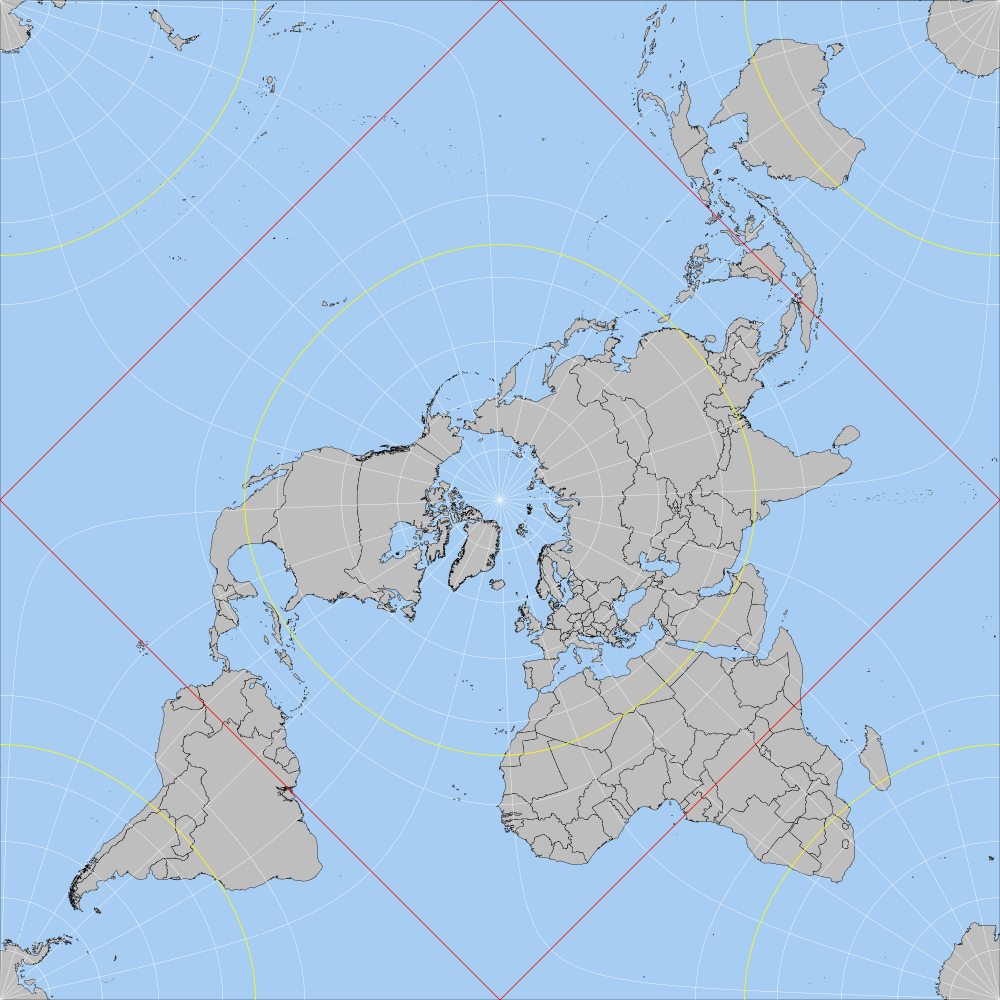
I'm using this algorithm for Peirce world map projection in R. I'm able to do some fine maps, for instance using 28 as the value for the lambda_0 parameter in function toPeirceQuincuncial, since this angle creates less land distortion and breaks no important islands (besides Antarctica, obviously). The algorithm is used like this:
# constants
pi<-acos(-1.0)
twopi<-2.0*pi
halfpi<-0.5*pi
degree<-pi / 180
halfSqrt2<-sqrt(2) / 2
quarterpi<-0.25 * pi
mquarterpi<--0.25 * pi
threequarterpi<-0.75 * pi
mthreequarterpi<--0.75 * pi
radian<-180/pi
sqrt2<-sqrt(2)
sqrt8<-2. * sqrt2
halfSqrt3<-sqrt(3) / 2
PeirceQuincuncialScale<-3.7081493546027438 ;# 2*K(1/2)
PeirceQuincuncialLimit<-1.8540746773013719 ;# K(1/2)
ellFaux<-function(cos_phi,sin_phi,k){
x<-cos_phi * cos_phi
y<-1.0 - k * k * sin_phi * sin_phi
z<-1.0
rf<-ellRF(x,y,z)
return(sin_phi * rf)
}
ellRF<-function(x,y,z){
if (x < 0.0 || y < 0.0 || z < 0.0) {
print("Negative argument to Carlson's ellRF")
print("ellRF negArgument")
}
delx<-1.0;
dely<-1.0;
delz<-1.0
while(abs(delx) > 0.0025 || abs(dely) > 0.0025 || abs(delz) > 0.0025) {
sx<-sqrt(x)
sy<-sqrt(y)
sz<-sqrt(z)
len<-sx * (sy + sz) + sy * sz
x<-0.25 * (x + len)
y<-0.25 * (y + len)
z<-0.25 * (z + len)
mean<-(x + y + z) / 3.0
delx<-(mean - x) / mean
dely<-(mean - y) / mean
delz<-(mean - z) / mean
}
e2<-delx * dely - delz * delz
e3<-delx * dely * delz
return((1.0 + (e2 / 24.0 - 0.1 - 3.0 * e3 / 44.0) * e2+ e3 / 14) / sqrt(mean))
}
toPeirceQuincuncial<-function(lambda,phi,lambda_0=20.0){
# Convert latitude and longitude to radians relative to the
# central meridian
lambda<-lambda - lambda_0 + 180
if (lambda < 0.0 || lambda > 360.0) {
lambda<-lambda - 360 * floor(lambda / 360)
}
lambda<-(lambda - 180) * degree
phi<-phi * degree
# Compute the auxiliary quantities 'm' and 'n'. Set 'm' to match
# the sign of 'lambda' and 'n' to be positive if |lambda| > pi/2
cos_phiosqrt2<-halfSqrt2 * cos(phi)
cos_lambda<-cos(lambda)
sin_lambda<-sin(lambda)
cos_a<-cos_phiosqrt2 * (sin_lambda + cos_lambda)
cos_b<-cos_phiosqrt2 * (sin_lambda - cos_lambda)
sin_a<-sqrt(1.0 - cos_a * cos_a)
sin_b<-sqrt(1.0 - cos_b * cos_b)
cos_a_cos_b<-cos_a * cos_b
sin_a_sin_b<-sin_a * sin_b
sin2_m<-1.0 + cos_a_cos_b - sin_a_sin_b
sin2_n<-1.0 - cos_a_cos_b - sin_a_sin_b
if (sin2_m < 0.0) {
sin2_m<-0.0
}
sin_m<-sqrt(sin2_m)
if (sin2_m > 1.0) {
sin2_m<-1.0
}
cos_m<-sqrt(1.0 - sin2_m)
if (sin_lambda < 0.0) {
sin_m<--sin_m
}
if (sin2_n < 0.0) {
sin2_n<-0.0
}
sin_n<-sqrt(sin2_n)
if (sin2_n > 1.0) {
sin2_n<-1.0
}
cos_n<-sqrt(1.0 - sin2_n)
if (cos_lambda > 0.0) {
sin_n<--sin_n
}
# Compute elliptic integrals to map the disc to the square
x<-ellFaux(cos_m,sin_m,halfSqrt2)
y<-ellFaux(cos_n,sin_n,halfSqrt2)
# Reflect the Southern Hemisphere outward
if(phi < 0) {
if (lambda < mthreequarterpi) {
y<-PeirceQuincuncialScale - y
} else if (lambda < mquarterpi) {
x<--PeirceQuincuncialScale - x
} else if (lambda < quarterpi) {
y<--PeirceQuincuncialScale - y
} else if (lambda < threequarterpi) {
x<-PeirceQuincuncialScale - x
} else {
y<-PeirceQuincuncialScale - y
}
}
# Rotate the square by 45 degrees to fit the screen better
X<-(x - y) * halfSqrt2
Y<-(x + y) * halfSqrt2
res<-list(X,Y)
return(res)
}
library(rgdal)
ang <- 28
p <- readOGR('~/R/shp','TM_WORLD_BORDERS-0.3') # read world shapefile
for (p1 in 1:length(p@polygons)) {
for (p2 in 1:length(p@polygons[[p1]]@Polygons)) {
for (p3 in 1:nrow(p@polygons[[p1]]@Polygons[[p2]]@coords)) {
pos <- toPeirceQuincuncial(p@polygons[[p1]]@Polygons[[p2]]@coords[p3,1],
p@polygons[[p1]]@Polygons[[p2]]@coords[p3,2],ang)
p@polygons[[p1]]@Polygons[[p2]]@coords[p3,1] <- pos[[1]][1]
p@polygons[[p1]]@Polygons[[p2]]@coords[p3,2] <- pos[[2]][1]
}
}
}
z <- toPeirceQuincuncial(0,-90,ang)[[1]][1]
p@bbox[,1] <- -z
p@bbox[,2] <- z
# plotting the map
par(mar=c(0,0,0,0),bg='#a7cdf2',xaxs='i',yaxs='i')
plot(p,col='gray',lwd=.5)
for (lon in 15*1:24) { # meridians
pos <- 0
posAnt <- 0
for (lat in -90:90) {
if (length(pos) == 2) {
posAnt <- pos
}
pos <- toPeirceQuincuncial(lon,lat,ang)
if (length(posAnt) == 2) {
segments(pos[[1]][1],pos[[2]][1],posAnt[[1]][1],posAnt[[2]][1],col='white',lwd=.5)
}
}
}
lats <- 15*1:5
posS <- matrix(0,length(lats),2)
posST <- 0
pos0 <- 0
posN <- matrix(0,length(lats),2)
posNT <- 0
for (lon in 0:360) {
posAntS <- posS
posAntST <- posST
posAnt0 <- pos0
posAntN <- posN
posAntNT <- posNT
pos0 <- unlist(toPeirceQuincuncial(lon,0,ang))
posST <- unlist(toPeirceQuincuncial(lon,-23.4368,ang))
posNT <- unlist(toPeirceQuincuncial(lon,23.4368,ang))
for (i in 1:length(lats)) {
posS[i,] <- unlist(toPeirceQuincuncial(lon,-lats[i],ang))
posN[i,] <- unlist(toPeirceQuincuncial(lon,lats[i],ang))
}
if (lon > 0) {
segments(pos0[1],pos0[2],posAnt0[1],posAnt0[2],col='red',lwd=1)
segments(posNT[1],posNT[2],posAntNT[1],posAntNT[2],col='yellow')
for (i in 1:length(lats)) {
segments(posN[i,1],posN[i,2],posAntN[i,1],posAntN[i,2],col='white',lwd=.5)
}
if (!(lon %in% round(90*(0:3+.5)+ang))) {
for (i in 1:length(lats)) {
segments(posS[i,1],posS[i,2],posAntS[i,1],posAntS[i,2],col='white',lwd=.5)
}
segments(posST[1],posST[2],posAntST[1],posAntST[2],col='yellow')
} else {
for (i in 1:length(lats)) {
posS[i,] <- unlist(toPeirceQuincuncial(lon-0.001,-lats[i],ang))
segments(posS[i,1],posS[i,2],posAntS[i,1],posAntS[i,2],col='white',lwd=.5)
posS[i,] <- unlist(toPeirceQuincuncial(lon,-lats[i],ang))
}
posST <- unlist(toPeirceQuincuncial(lon-0.001,-23.4368,ang))
segments(posST[1],posST[2],posAntST[1],posAntST[2],col='yellow')
posST <- unlist(toPeirceQuincuncial(lon,-23.4368,ang))
}
}
}
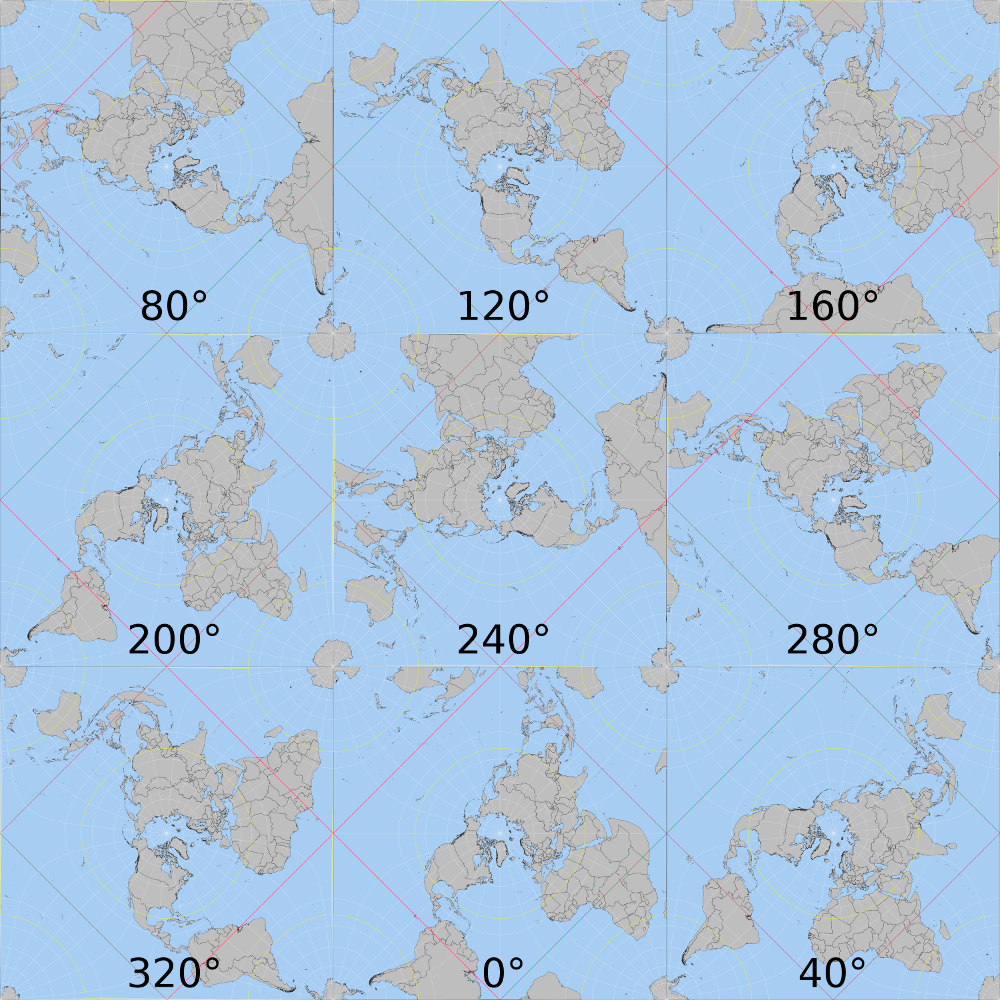
Playing with different values for lambda_0, I've found out that I apparently cannot choose any value I want. It seems that the function will only work with half the possibilities I thought it did.
Numbers indicate values of lambda_0. As you can see, North America moves clockwise from right to left between 80° and 200°, and starts the same movement again between 240° and 40°.
How can I change the algorithm to allow for any angle I want (for instance, North America pointing up)?

ang. And the only package used isrgdal. I've added it to the code, thank you for the remind. – Knapshofile, you get an error running it :Error in segments(pos[[1]][1], pos[[2]][1], posAnt[[1]][1], posAnt[[2]][1], : plot.new has not been called yet– Vivyanneparand the first call toplot). Now I think it's fine. – Knap