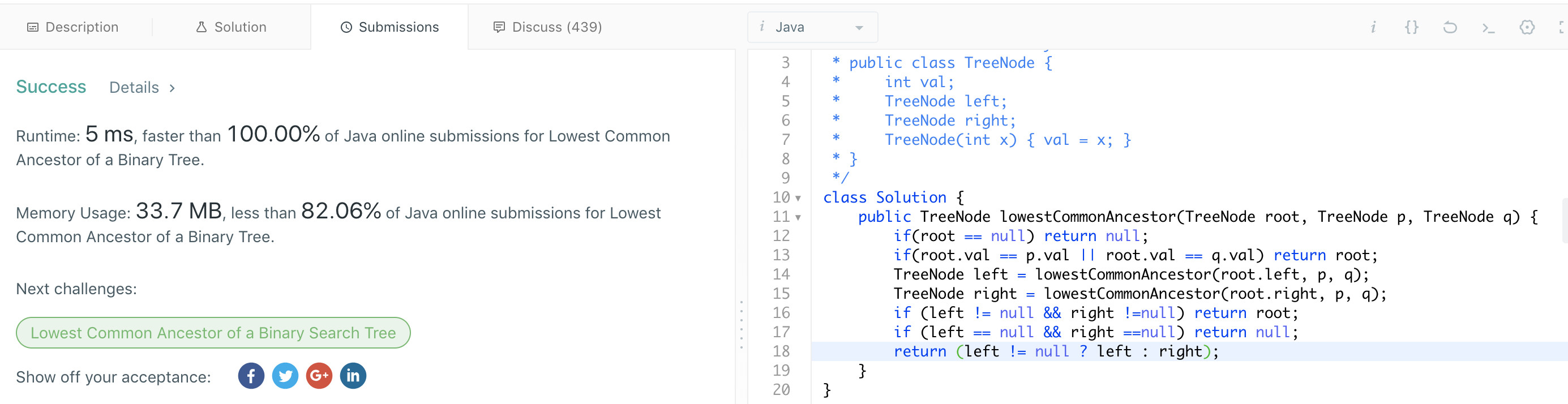
Here are two approaches in c# (.net) (both discussed above) for reference:
Recursive version of finding LCA in binary tree (O(N) - as at most each node is visited)
(main points of the solution is LCA is (a) only node in binary tree where both elements reside either side of the subtrees (left and right) is LCA. (b) And also it doesn't matter which node is present either side - initially i tried to keep that info, and obviously the recursive function become so confusing. once i realized it, it became very elegant.
Searching both nodes (O(N)), and keeping track of paths (uses extra space - so, #1 is probably superior even thought the space is probably negligible if the binary tree is well balanced as then extra memory consumption will be just in O(log(N)).
so that the paths are compared (essentailly similar to accepted answer - but the paths is calculated by assuming pointer node is not present in the binary tree node)
Just for the completion (not related to question), LCA in BST (O(log(N))
Tests
Recursive:
private BinaryTreeNode LeastCommonAncestorUsingRecursion(BinaryTreeNode treeNode,
int e1, int e2)
{
Debug.Assert(e1 != e2);
if(treeNode == null)
{
return null;
}
if((treeNode.Element == e1)
|| (treeNode.Element == e2))
{
//we don't care which element is present (e1 or e2), we just need to check
//if one of them is there
return treeNode;
}
var nLeft = this.LeastCommonAncestorUsingRecursion(treeNode.Left, e1, e2);
var nRight = this.LeastCommonAncestorUsingRecursion(treeNode.Right, e1, e2);
if(nLeft != null && nRight != null)
{
//note that this condition will be true only at least common ancestor
return treeNode;
}
else if(nLeft != null)
{
return nLeft;
}
else if(nRight != null)
{
return nRight;
}
return null;
}
where above private recursive version is invoked by following public method:
public BinaryTreeNode LeastCommonAncestorUsingRecursion(int e1, int e2)
{
var n = this.FindNode(this._root, e1);
if(null == n)
{
throw new Exception("Element not found: " + e1);
}
if (e1 == e2)
{
return n;
}
n = this.FindNode(this._root, e2);
if (null == n)
{
throw new Exception("Element not found: " + e2);
}
var node = this.LeastCommonAncestorUsingRecursion(this._root, e1, e2);
if (null == node)
{
throw new Exception(string.Format("Least common ancenstor not found for the given elements: {0},{1}", e1, e2));
}
return node;
}
Solution by keeping track of paths of both nodes:
public BinaryTreeNode LeastCommonAncestorUsingPaths(int e1, int e2)
{
var path1 = new List<BinaryTreeNode>();
var node1 = this.FindNodeAndPath(this._root, e1, path1);
if(node1 == null)
{
throw new Exception(string.Format("Element {0} is not found", e1));
}
if(e1 == e2)
{
return node1;
}
List<BinaryTreeNode> path2 = new List<BinaryTreeNode>();
var node2 = this.FindNodeAndPath(this._root, e2, path2);
if (node1 == null)
{
throw new Exception(string.Format("Element {0} is not found", e2));
}
BinaryTreeNode lca = null;
Debug.Assert(path1[0] == this._root);
Debug.Assert(path2[0] == this._root);
int i = 0;
while((i < path1.Count)
&& (i < path2.Count)
&& (path2[i] == path1[i]))
{
lca = path1[i];
i++;
}
Debug.Assert(null != lca);
return lca;
}
where FindNodeAndPath is defined as
private BinaryTreeNode FindNodeAndPath(BinaryTreeNode node, int e, List<BinaryTreeNode> path)
{
if(node == null)
{
return null;
}
if(node.Element == e)
{
path.Add(node);
return node;
}
var n = this.FindNodeAndPath(node.Left, e, path);
if(n == null)
{
n = this.FindNodeAndPath(node.Right, e, path);
}
if(n != null)
{
path.Insert(0, node);
return n;
}
return null;
}
BST (LCA) - not related (just for completion for reference)
public BinaryTreeNode BstLeastCommonAncestor(int e1, int e2)
{
//ensure both elements are there in the bst
var n1 = this.BstFind(e1, throwIfNotFound: true);
if(e1 == e2)
{
return n1;
}
this.BstFind(e2, throwIfNotFound: true);
BinaryTreeNode leastCommonAcncestor = this._root;
var iterativeNode = this._root;
while(iterativeNode != null)
{
if((iterativeNode.Element > e1 ) && (iterativeNode.Element > e2))
{
iterativeNode = iterativeNode.Left;
}
else if((iterativeNode.Element < e1) && (iterativeNode.Element < e2))
{
iterativeNode = iterativeNode.Right;
}
else
{
//i.e; either iterative node is equal to e1 or e2 or in between e1 and e2
return iterativeNode;
}
}
//control will never come here
return leastCommonAcncestor;
}
Unit Tests
[TestMethod]
public void LeastCommonAncestorTests()
{
int[] a = { 13, 2, 18, 1, 5, 17, 20, 3, 6, 16, 21, 4, 14, 15, 25, 22, 24 };
int[] b = { 13, 13, 13, 2, 13, 18, 13, 5, 13, 18, 13, 13, 14, 18, 25, 22};
BinarySearchTree bst = new BinarySearchTree();
foreach (int e in a)
{
bst.Add(e);
bst.Delete(e);
bst.Add(e);
}
for(int i = 0; i < b.Length; i++)
{
var n = bst.BstLeastCommonAncestor(a[i], a[i + 1]);
Assert.IsTrue(n.Element == b[i]);
var n1 = bst.LeastCommonAncestorUsingPaths(a[i], a[i + 1]);
Assert.IsTrue(n1.Element == b[i]);
Assert.IsTrue(n == n1);
var n2 = bst.LeastCommonAncestorUsingRecursion(a[i], a[i + 1]);
Assert.IsTrue(n2.Element == b[i]);
Assert.IsTrue(n2 == n1);
Assert.IsTrue(n2 == n);
}
}