You are off the road... Singular value decomposition is applied to model matrix X rather than normal matrix X'X. The following is the correct procedure:
![svd for ols]()
So when writing an R function, we should do
svdOLS <- function (X, y) {
SVD <- svd(X)
V <- SVD$v
U <- SVD$u
D <- SVD$d
## regression coefficients `b`
## use `crossprod` for `U'y`
## use recycling rule for row rescaling of `U'y` by `D` inverse
## use `as.numeric` to return vector instead of matrix
b <- as.numeric(V %*% (crossprod(U, y) / D))
## residuals
r <- as.numeric(y - X %*% b)
## R-squared
RSS <- crossprod(r)[1]
TSS <- crossprod(y - mean(y))[1]
R2 <- 1 - RSS / TSS
## multiple return via a list
list(coefficients = b, residuals = r, R2 = R2)
}
Let's have a test
## toy data
set.seed(0)
x1 <- rnorm(50); x2 <- rnorm(50); x3 <- rnorm(50); y <- rnorm(50)
X <- model.matrix(~ x1 + x2 + x3)
## fitting linear regression: y ~ x1 + x2 + x3
svdfit <- svdOLS(X, y)
#$coefficients
#[1] 0.14203754 -0.05699557 -0.01256007 0.09776255
#
#$residuals
# [1] 1.327108410 -1.400843739 -0.071885339 2.285661880 0.882041795
# [6] -0.535230752 -0.927750996 0.262674650 -0.133878558 -0.559783412
#[11] 0.264204296 -0.581468657 2.436913000 1.517601798 0.774515419
#[16] 0.447774149 -0.578988327 0.664690723 -0.511052627 -1.233302697
#[21] 1.740216739 -1.065592673 -0.332307898 -0.634125164 -0.975142054
#[26] 0.344995480 -1.748393187 -0.414763742 -0.680473508 -1.547232557
#[31] -0.383685601 -0.541602452 -0.827267878 0.894525453 0.359062906
#[36] -0.078656943 0.203938750 -0.813745178 -0.171993018 1.041370294
#[41] -0.114742717 0.034045040 1.888673004 -0.797999080 0.859074345
#[46] 1.664278354 -1.189408794 0.003618466 -0.527764821 -0.517902581
#
#$R2
#[1] 0.008276773
On the other hand, we can use .lm.fit to check correctness:
qrfit <- .lm.fit(X, y)
which is exactly the same on coefficients and residuals:
all.equal(svdfit$coefficients, qrfit$coefficients)
# [1] TRUE
all.equal(svdfit$residuals, qrfit$residuals)
# [1] TRUE

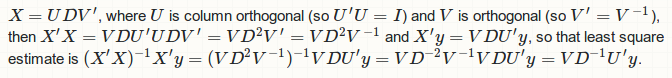
xandXare different. The first line of your function usesA, butAis not input. Where does it come from? I'm also not sure whatlabelsis - isn't this code you wrote? What is it supposed to do? – Sheronsherourdlabels. Yes and sorry, A was a test matrix. But my question was already answered below, thanks anyway! – Topless