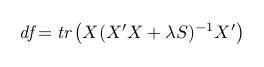smooth.spline(): fitted model does not match user-specified degree of freedom

Question

Here is the code I ran

fun <- function(x) {1 + 3*sin(4*pi*x-pi)}
set.seed(1)
num.samples <- 1000
x <- runif(num.samples)
y <- fun(x) + rnorm(num.samples) * 1.5
fit <- smooth.spline(x, y, all.knots=TRUE, df=3)

Despite df=3, when I checked the fitted model, the output was

Call:
smooth.spline(x = x, y = y, df = 3, all.knots = TRUE)
Smoothing Parameter  spar= 1.499954  lambda= 0.002508571 (26 iterations)
Equivalent Degrees of Freedom (Df): 9.86422

Could someone please help? Thanks!

Cher

Have you considered the possibility that the degrees of freedom you provide is a goal that the algorithm tries to optimize towards (among other criteria) and that is simply as close as the algorithm could get? – Stiffen

Answer 1

Note that from R-3.4.0 (2017-04-21), smooth.spline can accept direct specification of λ by a newly added argument lambda. But it will still be converted to the internal one spar during estimation. So the following answer is not affected.

---

Smoothing parameter λ / spar lies in the centre of smoothness control

Smoothness is controlled by smoothing parameter λ.smooth.spline() uses an internal smoothing parameter spar rather than λ:

spar = s0 + 0.0601 * log(λ)

Such logarithm transform is necessary in order to do unconstrained minimization, like GCV/CV. User can specify spar to indirectly specify λ. When spar grows linearly, λ will grow exponentially. Thus there is rarely the need for using large spar value.

The degree of freedom df, is also defined in terms of λ:

where X is the model matrix with B-spline basis and S is the penalty matrix.

You can have a check on their relationships with your dataset:

spar <- seq(1, 2.5, by = 0.1)
a <- sapply(spar, function (spar_i) unlist(smooth.spline(x, y, all.knots=TRUE, spar = spar_i)[c("df","lambda")]))

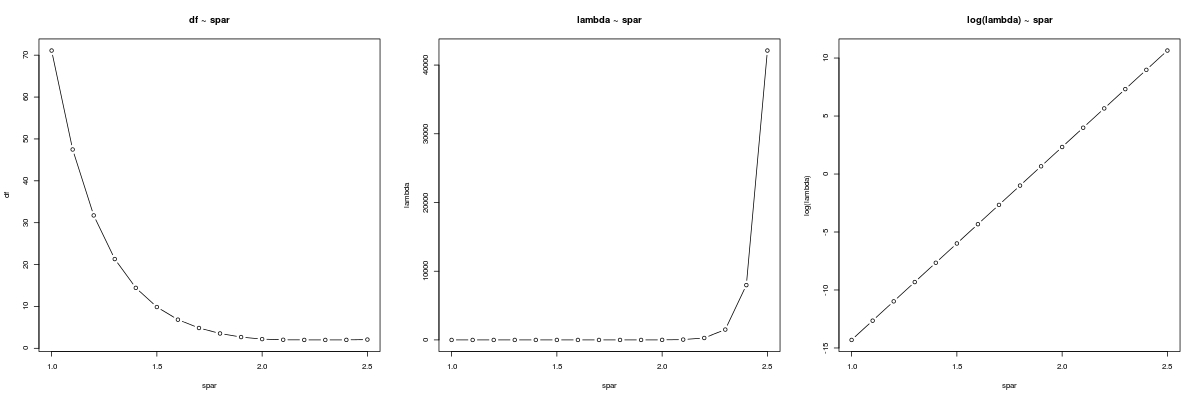
Let's sketch df ~ spar, λ ~ spar and log(λ) ~ spar:

par(mfrow = c(1,3))
plot(spar, a[1, ], type = "b", main = "df ~ spar",
     xlab = "spar", ylab = "df")
plot(spar, a[2, ], type = "b", main = "lambda ~ spar",
     xlab = "spar", ylab = "lambda")
plot(spar, log(a[2,]), type = "b", main = "log(lambda) ~ spar",
     xlab = "spar", ylab = "log(lambda)")

Note the radical growth of λ with spar, the linear relationship between log(λ) and spar, and the relatively smooth relationship between df and spar.

---

smooth.spline() fitting iterations for spar

If we manually specify the value of spar, like what we did in the sapply(), no fitting iterations is done for selecting spar; otherwise smooth.spline() needs iterate through a number of spar values. If we

• specify cv = TRUE / FALSE, fitting iterations aims to minimize CV/GCV score;
• specify df = mydf, fitting iterations aims to minimize (df(spar) - mydf) ^ 2.

Minimizing GCV is easy to follow. We don't care about the GCV score, but care the corresponding spar. On the contrary, when minimizing (df(spar) - mydf)^2, we often care about the df value at the end of iteration rather than spar! But bearing in mind that this is an minimization problem, we are never guaranteed that the final df matches our target value mydf.

---

Why you put df = 3, but get df = 9.864?

The end of iteration, could either implies hitting a minimum, or reaching searching boundary, or reaching maximum number of iterations.

We are far from maximum iterations limit (default 500); yet we do not hit the minimum. Well, we might reach the boundary.

Do not focus on df, think about spar.

smooth.spline(x, y, all.knots=TRUE, df=3)$spar   # 1.4999

According to ?smooth.spline, by default, smooth.spline() searches spar between [-1.5, 1.5]. I.e., when you put df = 3, minimization terminates at the searching boundary, rather than hitting df = 3.

Have a look at our graph of the relationship between df and spar, again. From the figure, it looks like that we need some spar value near 2 in order to result in df = 3.

Let's use control.spar argument:

fit <- smooth.spline(x, y, all.knots=TRUE, df=3, control.spar = list(high = 2.5))
# Smoothing Parameter  spar= 1.859066  lambda= 0.9855336 (14 iterations)
# Equivalent Degrees of Freedom (Df): 3.000305

Now you see, you end up with df = 3. And we need a spar = 1.86.

---

A better suggestion: Do not use all.knots = TRUE

Look, you have 1000 data. With all.knots = TRUE you will use 1000 parameters. Wishing to end up with df = 3 implies that 997 out of 1000 parameters are suppressed. Imagine how large a λ hence spar you need!

Try using penalized regression spline instead. Suppressing 200 parameters to 3 is definitely much easier:

fit <- smooth.spline(x, y, nknots = 200, df=3)  ## using 200 knots
# Smoothing Parameter  spar= 1.317883  lambda= 0.9853648 (16 iterations)
# Equivalent Degrees of Freedom (Df): 3.000386

Now, you end up with df = 3 without spar control.

Weeper