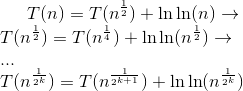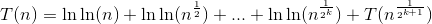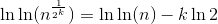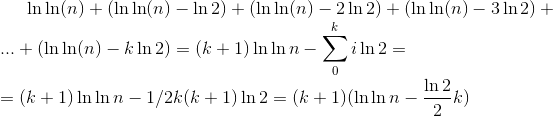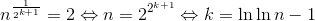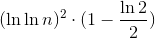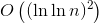Solve recurrence: T(n) = T(n^(1/2)) + Θ(lg lg n) [closed]

Question

Started learning algorithms. I understand how to find theta-notation from a 'regular recurrence' like T(n) = Tf(n) + g(n). But I am lost with this recurrence: problem 1-2e:

T(n) = T(√n) + Θ(lg lg n)

How do I choose the method to find theta? And what, uh, this recurrence is? I just do not quite understand notation-inside-a-recurrence thing.

Peek

Stack Overflow is a site for programming and development questions. This question appears to be off-topic because it is not about programming or development. See What topics can I ask about here in the Help Center. Perhaps Mathematics Stack Exchange would be a better place to ask. – Uta

Oh wow, what a blast from the past! This is a general computer science question (measuring theta notation for algorithms), where should it be moved? This doesn't belong on Mathematics since this is not a mathematics question. Oh, and I see similar questions live on StackOverflow -- #3755. – Peek

Yeah, sorry about that. A fellow asked a similar question that was poor quality. His question was closed as off-topic. In retaliation he cited your question and you got dragged down with him. – Uta

Answer 1

This is a great place to use a variable substitution. We begin with

T(n) = T(√n) + Θ(log log n),

where the parameter n decays by a square root factor. When you see something like this, a common transform that works well is to define a new recurrence by setting S(m) = T(2^m). If we do that here, we get the following:

S(m) = T(2^m)

= T(√(2^m)) + Θ(log log 2^m)

= T(2^m/2) + Θ(log m)

= S(m / 2) + Θ(log m).

In other words, we now have the recurrence

S(m) = S(m / 2) + Θ(log m).

This recurrence seems a lot easier to work with, since we no longer have that square root term shrinking things down. And in particular, this happens to be something the Master Theorem takes care of. Specifically, we have a = 1, b = 2, and d = 0. (Why do we have d = 0? Because we can think of Θ(log m) as m⁰ Θ(log m)). The Master Theorem then tells us that this solves to

S(m) = Θ((log m)²).

We've just solved the recurrence S(m), but we were interested in solving the recurrence T(n). How do we connect them? Well, since S(m) = T(2^m), we can - assuming n is a perfect power of two - rewrite this as S(log n) = T(n). That then lets us see that

T(n) = S(log n)

= Θ((log log n)²),

which is the solution of the recurrence.

Fillip

from lg k + (lg k) - 1 + (lg k) - 2 + (lg k) - 3 + ... + (lg k) - lg k How did you got Θ((lg k)2) ? – Gravid

This follows from the sum 1 + 2 + 3 + ... + n = n(n+1)/2, plugging in n = lg k. – Fillip

Sorry I still didn't get it properly. Can u pls provide step wise reduction from lg k + (lg k) - 1 + (lg k) - 2 + (lg k) - 3 + ... + (lg k) - lg k pls ? Yeah I know that summation . But How can you reduce this still ? Please make it clear – Gravid

@AkhilNadhPC Notice that (lg k) - 1 + (lg k) - 2 + ... + (lg k) - (lg k), written backwards, is 0 + 1 + 2 + ... + (lg k) - 2 + (lg k) - 1 + lg k. – Fillip

What I understood is upto this (lg k) - 1 + (lg k) - 2 + ... + (lg k) - (lg k), = (lg k) +(lg k) + ..... +(lg k) -( 1+2+3+4+.... ) = (lg k) +(lg k) + ..... +(lg k) - m(m+1) / 2 How can u relate m = log k ? (here) – Gravid

That would work too. Notice that that simplifies to (lg k)^2 - m(m+1)/2, with m = lg k. Then you have (lg k)^2 - (lg k)(lg k + 1) / 2 ~= (lg k)^2 / 2. – Fillip

Answer 2

Here is how to solve it using math. I will be using lnln(n) instead of O(lnln(n)). This is mostly to reduce the length of the formulae and you can do absolutely the same with big-O. So:

Which means that:

,

now to transform this big summation notice that

The whole lnln(n) sum can be transformed as:

And our only problem is to find some connection between n and k, which can be easily derived from the latest T(...) term.

---

To do this we have to to find a reasonable bound condition for the latest term. This can be done by trying a couple of integers like 0, 1, 2. With 2 you have:

---

Substituting k to our previous equation you will see that the biggest term is:

and therefore the complexity is:

P.S. you can see a solution to a similar recurrence here

Demented