Principal Component Analysis with Eigen Library

Question

I'm trying to compute the 2 major principal components from a dataset in C++ with Eigen.

The way I do it at the moment is to normalize the data between [0, 1] and then center the mean. After that I compute the covariance matrix and run an eigenvalue decomposition on it. I know SVD is faster, but I'm confused about the computed components.

Here is the major code about how I do it (where traindata is my MxN sized input matrix):

Eigen::VectorXf normalize(Eigen::VectorXf vec) {
  for (int i = 0; i < vec.size(); i++) { // normalize each feature.
      vec[i] = (vec[i] - minCoeffs[i]) / scalingFactors[i];
  }
  return vec;
}

// Calculate normalization coefficients (globals of type Eigen::VectorXf). 
maxCoeffs = traindata.colwise().maxCoeff();
minCoeffs = traindata.colwise().minCoeff();
scalingFactors = maxCoeffs - minCoeffs;

// For each datapoint.
for (int i = 0; i < traindata.rows(); i++) { // Normalize each datapoint.
  traindata.row(i) = normalize(traindata.row(i));
}

// Mean centering data.
Eigen::VectorXf featureMeans = traindata.colwise().mean();
Eigen::MatrixXf centered = traindata.rowwise() - featureMeans;

// Compute the covariance matrix.
Eigen::MatrixXf cov = centered.adjoint() * centered;
cov = cov / (traindata.rows() - 1);

Eigen::SelfAdjointEigenSolver<Eigen::MatrixXf> eig(cov);
// Normalize eigenvalues to make them represent percentages.
Eigen::VectorXf normalizedEigenValues =  eig.eigenvalues() / eig.eigenvalues().sum();


// Get the two major eigenvectors and omit the others.
Eigen::MatrixXf evecs = eig.eigenvectors();
Eigen::MatrixXf pcaTransform = evecs.rightCols(2);


// Map the dataset in the new two dimensional space.
traindata = traindata * pcaTransform;

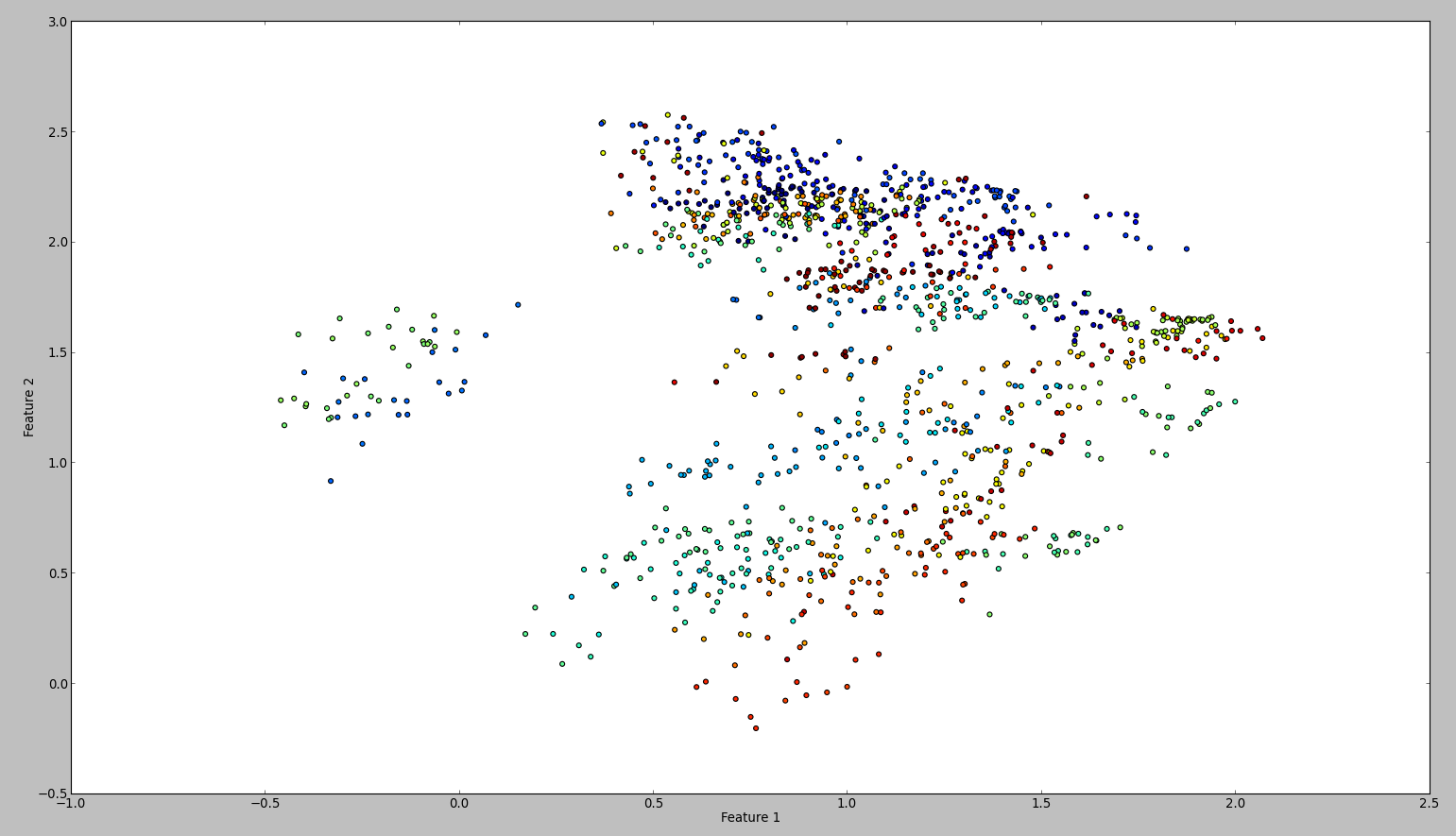
The result of this code is something like this:

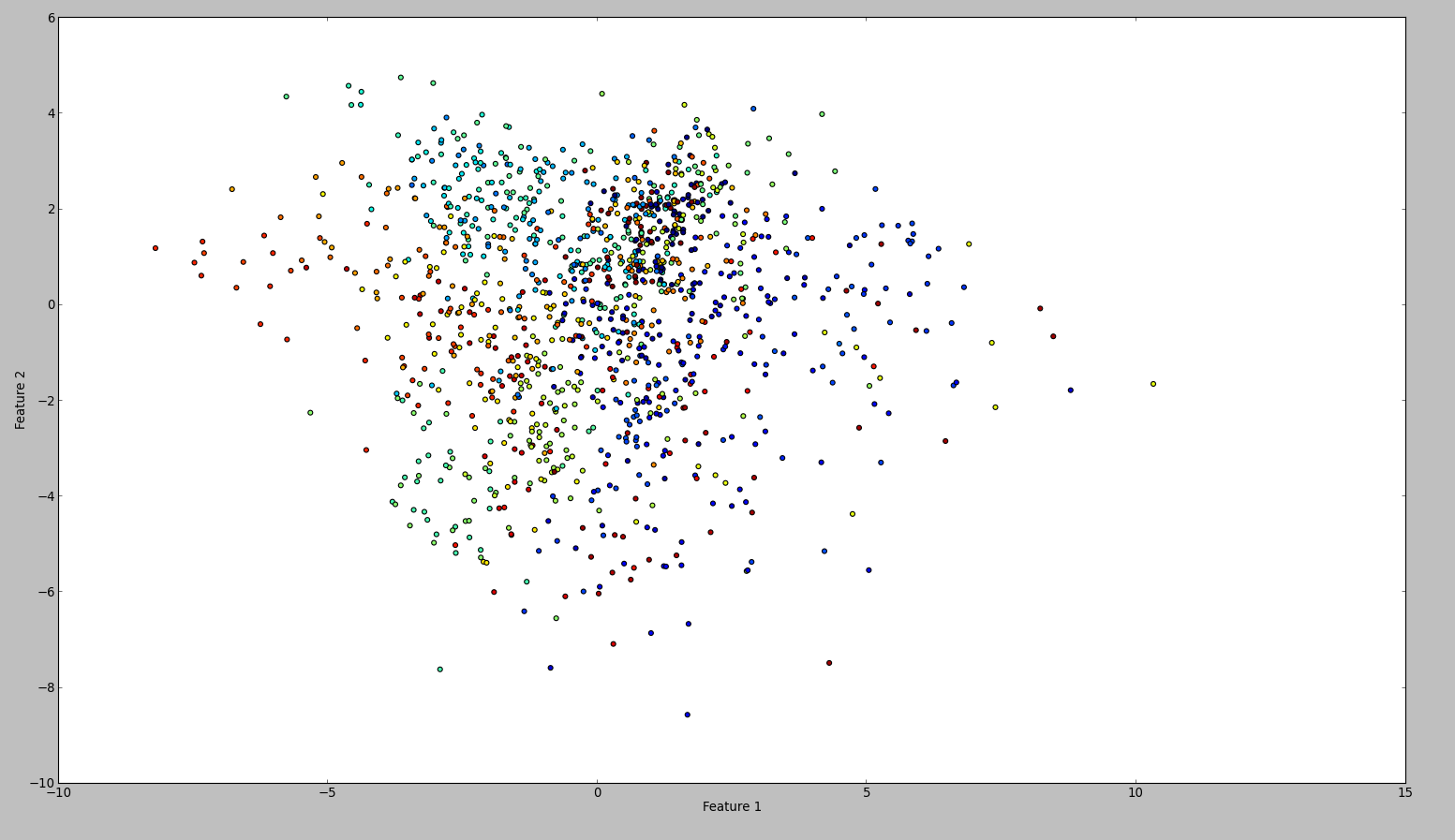
To confirm my results, I tried the same with WEKA. So what I did is to use the normalize and the center filter, in this order. Then the principal component filter and save + plot the output. The result is this:

Technically I should have done the same, however the outcome is so different. Can anyone see if I made a mistake?

Malathion

One thing to add: I'm quite sure that WEKA is using SVD. But this should not explain the difference in the outcome or? – Malathion

I realize this question is old, however do you know by any chance, which paper (or other source) you used for this implementation? – Broca

I think I just looked it up on Wikipedia and multiple other pages that I found via search. But not to a scientific paper. But if you need more trustworthy sources I'm sure you can find the procedure in plenty of maths/stats/data analysis books. – Malathion

I am indeed looking for this specific source. Thanks for the quick response. – Broca

Answer 1

The reason was that Weka standardized the dataset. This means it scales each feature's variance to unit variance. When I did this, the plots looked the same. Technically my approach was correct as well.

Malathion

could you please also post the running code? Thanks. – Supposititious

I'll have a look, I don't know if I still have access to that piece of code and which version I used eventually. But I surely talked about classic standardization, which is well defined: en.wikipedia.org/wiki/Feature_scaling#Standardization – Malathion

Answer 2

When scaling to 0,1, you modify the local variable vec but forgot to update traindata.

Moreover, this can be done more easily this way:

RowVectorXf minCoeffs = traindata.colwise().maxCoeff();
RowVectorXf minCoeffs = traindata.colwise().minCoeff();
RowVectorXf scalingFactors = maxCoeffs - minCoeffs;
traindata = (traindata.rowwise()-minCoeffs).array().rowwise() / scalingFactors.array();

that is, using row-vectors and array features.

Let me also add that the symmetric eigenvalue decomposition is actually faster than SVD. The true advantage of SVD in this case is that it avoids squaring the entries, but since your input data are normalized and centered, and that you only care about the largest eigenvalues, there is no accuracy concern here.

Namedropping

That was a mistake, in my big code I made a funciton call that's returning by value like this: traindata.row(i) = normalize(traindata.row(i));. Changed it here too to make sure there is no mistake. Thanks for the code simplification, I guessed it's somehow possible. Can you see another problem? – Malathion

Another question, my compiler tells me 'no match for ‘operator/’' when I run your code. I have Eigen3, seems there is no rowwise division or? – Malathion

this will throw division by zero if you have for 1 feature max = min, am I right? – Supposititious

Right, you need to replace zeros by ones in scalingFactors. – Namedropping