Transposition table in Monte Carlo Tree Search algorithm unintended effect on UCT score

Question

So I implemented a transposition table in a Monte Carlo Tree Search algorithm using UCT. This allows for keeping a cumulative reward value for a game state, no matter where, and how many times, it is encountered throughout the tree. This increases the quality of the information gathered on the particular game state.

Alas, I have noticed that this creates certain problem with the exploitation vs. exploration selection phase of UCT. In short, the UCT score assigned to a state, takes into account the ratio between the number of times the parent state was visited and the number of times the child (whom we are calculating the UCT score for) was visited. As you can see from this diagram,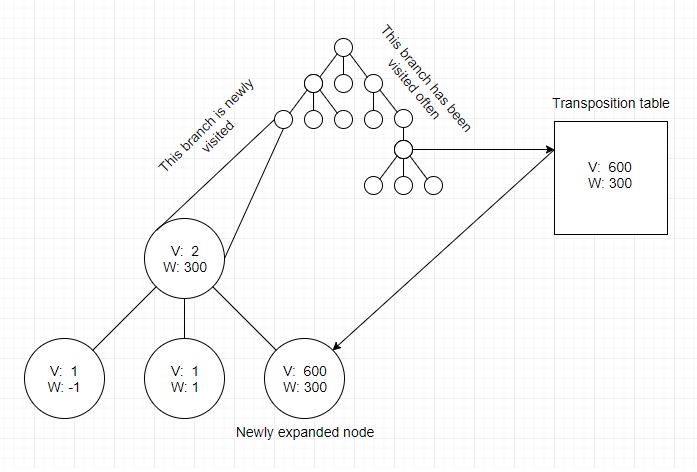 when pulling in a state from the transposition table into a newly created branch of the tree, that ratio is all out of whack, with the child state having been visited a great number of times (from elsewhere in the tree) and the parent state having been visited a much smaller amount of times, which should technically be impossible.

So, using a transposition table and persisting the cumulative reward value of a state helps the exploitation part of the algorithm make better choices, but at the same time it skews the exploitation part of the algorithm in a potentially harmful way. Are you aware of any ways to counteract this unintended problem?

Jacquejacquelin

Cross-posted: https://mcmap.net/q/1312577/-transposition-table-in-monte-carlo-tree-search-algorithm-unintended-effect-on-uct-score/781723, cs.stackexchange.com/q/91537/755. Please do not post the same question on multiple sites. Each community should have an honest shot at answering without anybody's time being wasted. – Privateer

My bad, I did not know that this was a rule. I was hoping to get ahead of the 'this question is out of scope for this community, you should try posting it on an other community' comment that I get every second question that I post ;-) – Jacquejacquelin

No problem, there's no way you would know. You can pick one site where you want it to appear. If you're happy with it appearing on SO, you don't need to do anything -- just letting you know for the future. If you'd prefer for it to appear on CS.SE instead of SO, you can delete the copy here on SO and then flag the copy on CS.SE to be re-opened. – Privateer

I would want it where there is the best chance to get some quality answers, but I don't know where that is, hence my posting it in both community. I guess let's leave it here and see what happens. – Jacquejacquelin

relevant paper: "UCD : Upper confidence bound for rooted directed acyclic graphs" hal.archives-ouvertes.fr/hal-01499672/document – Acutance

Answer 1

Intuitively, I expect you'll want to try the following.

For the exploitation part of UCT, you'll want to store and use the average scores W / V of child nodes. This average in its entirety can be shared through transpositions. So, in your example, you don't necessarily want to separately share the W = 300 and V = 600, but instead just share the average score W / V = 300 / 600 = 0.5. This means that, thanks to transpositions, you can share more accurate estimates of scores (estimates based on larger sample sizes).

For the exploration part of UCT, I think you'll want to use statistics "from the perspective" of the parent node (where you don't have a transposition), rather than the child node (which is a transposition of a node elsewhere in the tree). Instead of using visit counts of child nodes when selecting which child node to go to, this means you'll use visit counts collected per state + action pair in the parent node.

For example, consider we are in the node where you wrote V: 2, W: 300 (refer to this node as P), and we have to select a child node. The more standard implementation would loop over the children, and use the child node's visit counts. In your situation, I think it'd be better to instead loop over the actions in the node P, and keep track of visit counts for those actions instead of for the child nodes. In P, you'll not yet ever have taken the action leading to the transposition child node, so this visit count for the (P + action) pair will still be 0.

---

I do not personally have experience with the combination of MCTS + transpositions though, so you may wish to do additional research to see what others have come up with in the past. There are for example the following papers:

• Transpositions and Move Groups in Monte Carlo Tree Search
• BTT-Go: An Agent for Go That Uses a Transposition Table to Reduce the Simulations and the Supervision in the Monte-Carlo Tree Search
• And there may be more if you look around, not sure.

Thunderclap

Answer 2

I've implemented the following which worked well with an Alpha Zero style algorithm with Chess:

• Build the game tree as with traditional MCTS.
• Keep transposition table map from game states to their maximum visit count and value sum.
• When selecting an action, check if it was seen elsewhere with a greater visit count, and average out the value as (moveValueSum + transpositionValueSum) / (moveVisits + transpositionVisits).
  • If the current action has more visits than what is in the transposition table, then update the transposition table.

This way we don't sum across all visits of an action, rather we only average the action value with the single most visited instance of it.

Acutance

Good write-up about a theoretically sound solution, which keeps visit counts in edges instead of nodes: github.com/lightvector/KataGo/blob/master/docs/GraphSearch.md – Acutance