Draw a parallel line in R offset from a line

Question

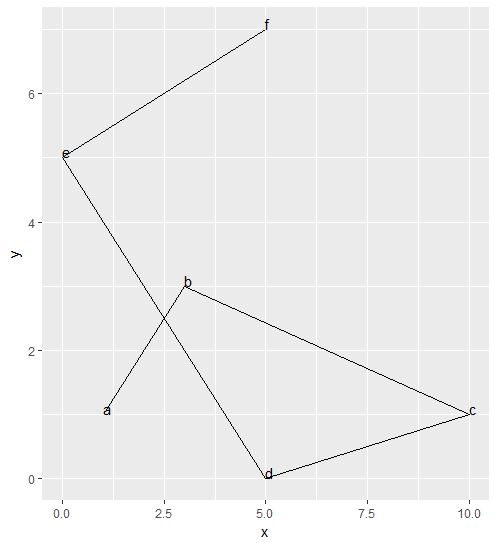
I have linestring which represent a driving journey down some streets. But I want to actually represent a cyclists journey, which is offset from the line i.e. they travel near the kerb of the road. I'm struggling with how to do it. I've made a reproducible piece of R code to illustrate.

## Let's say I have a route along some streets.
library(ggplot2)

## It can be described by this
data          <- data.frame(x = c(1,3,10,5,0,5),
                            y = c(1,3,1,0,5,7),
                            label = c('a', 'b', 'c', 'd', 'e', 'f'))
## Visualised by this
ggplot(data, aes(x, y)) +
  geom_path() +
  geom_text(aes(label=label),hjust=0, vjust=0)

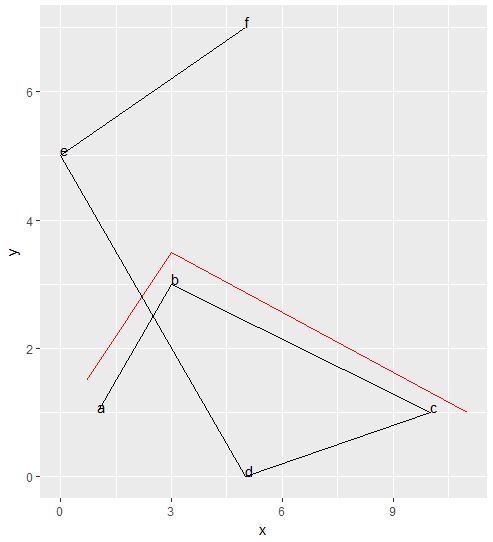
But what I want to do it model as though someone were cycling. Let's say they cycle 0.5 away from the centre line of the road, to the left but of course 'left' is relative to the direction of the line The start of the journey would actually look something like this Note the 'new_x' and 'new_y' are not mathmatically correct. They're estimations for illustrative purposes.

data          <- data.frame(x = c(1,3,10,5,0,5),
                            y = c(1,3,1,0,5,7),
                            new_x = c(0.7, 3, 10.5,NA, NA, NA) ,
                        new_y = c(1.5, 3.5, 1, NA, NA, NA),
                        label = c('a', 'b', 'c', 'd', 'e', 'f'))

## Visualised by this showing the old line and the new line
ggplot(data, aes(x, y)) +
  geom_path() +
  geom_text(aes(label=label),hjust=0, vjust=0) +
  geom_path(data = data, aes(new_x, new_y), colour='red')

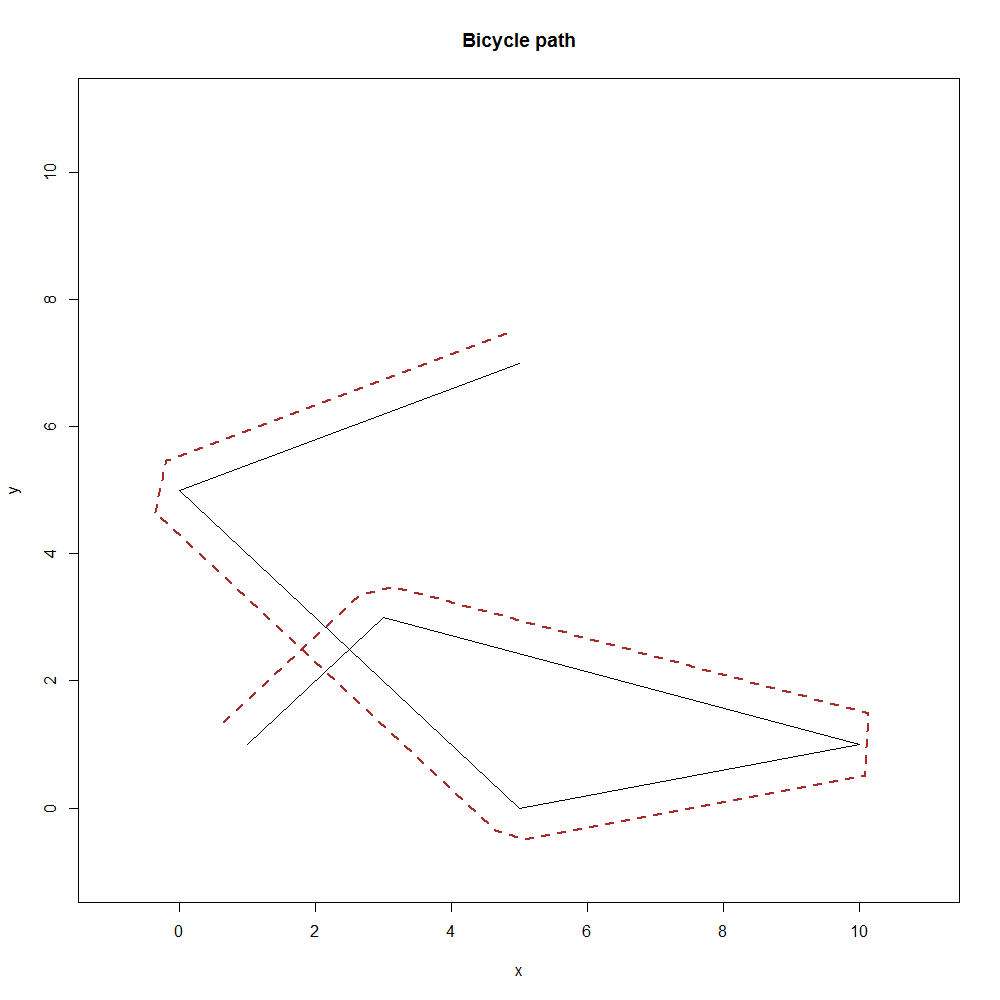
So the question is how do I correctly calculate new_x and new_y to create a continuous line representing a cyclists journey as offset from the centre of the road

Apeman

Answer 1

There is a package that provides offset calculation for splines: https://www.stat.auckland.ac.nz/~paul/Reports/VWline/offset-xspline/offset-xspline.html

Here is some very basic approximation. I purposely left the corners to be cut off since that is probably be a better approximation of how bikes will turn around the corner. Please also note that some extra steps will be needed if you need to calculate the "inward" shift:

x <-  c(1,3,10,5,0,5)
y <-  c(1,3,1,0,5,7)
d <- 0.5   # distance away from the road


# Given a vector (defined by 2 points) and the distance, 
# calculate a new vector that is distance away from the original 
segment.shift <- function(x, y, d){

  # calculate vector
  v <- c(x[2] - x[1],y[2] - y[1])

  # normalize vector
  v <- v/sqrt((v[1]**2 + v[2]**2))

  # perpendicular unit vector
  vnp <- c( -v[2], v[1] )

  return(list(x =  c( x[1] + d*vnp[1], x[2] + d*vnp[1]), 
              y =  c( y[1] + d*vnp[2], y[2] + d*vnp[2])))

}

plot(x,y, xlim=c(-1,11), ylim=c(-1,11), type="l", main= "Bicycle path" )

# allocate memory for the bike path
xn <- numeric( (length(x) - 1) * 2 )
yn <- numeric( (length(y) - 1) * 2 )

for ( i in 1:(length(x) - 1) ) {
  xs <- c(x[i], x[i+1])
  ys <- c(y[i], y[i+1])
  new.s <- segment.shift( xs, ys, d )
  xn[(i-1)*2+1] <- new.s$x[1] ; xn[(i-1)*2+2] <- new.s$x[2]
  yn[(i-1)*2+1] <- new.s$y[1] ; yn[(i-1)*2+2] <- new.s$y[2]
}

# draw the path
lines(xn, yn, col="brown", lwd =2, lty=2)

Nebraska

This looks amazing. So clever. Thank you Katia. Will have a play with it in the morning then mark this as the answer. Thanks again. – Apeman

what if we wanted to add multiple parallel lines x feet apart from each other? – Ezraezri