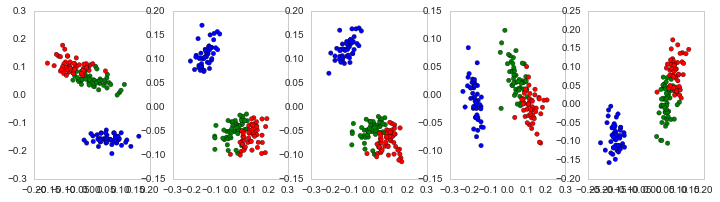
I'm trying to figure out how to implement Principal Coordinate Analysis with various distance metrics. I stumbled across both skbio and sklearn with implementations. I don't understand why sklearn's implementation is different everytime while skbio is the same? Is there a degree of randomness to Multidimensional Scaling and in particular Principal Coordinate Analysis? I see that all of the clusters are very similar but why are they different? Am I implementing this correctly?
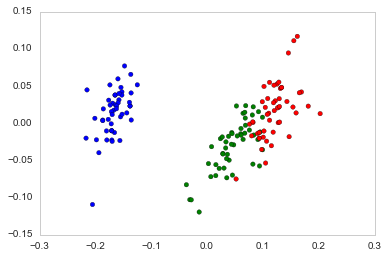
Running Principal Coordinate Analysis using Scikit-bio (i.e. Skbio) always gives the same results:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn import decomposition
import seaborn as sns; sns.set_style("whitegrid", {'axes.grid' : False})
import skbio
from scipy.spatial import distance
%matplotlib inline
np.random.seed(0)
# Iris dataset
DF_data = pd.DataFrame(load_iris().data,
index = ["iris_%d" % i for i in range(load_iris().data.shape[0])],
columns = load_iris().feature_names)
n,m = DF_data.shape
# print(n,m)
# 150 4
Se_targets = pd.Series(load_iris().target,
index = ["iris_%d" % i for i in range(load_iris().data.shape[0])],
name = "Species")
# Scaling mean = 0, var = 1
DF_standard = pd.DataFrame(StandardScaler().fit_transform(DF_data),
index = DF_data.index,
columns = DF_data.columns)
# Distance Matrix
Ar_dist = distance.squareform(distance.pdist(DF_data, metric="braycurtis")) # (n x n) distance measure
DM_dist = skbio.stats.distance.DistanceMatrix(Ar_dist, ids=DF_standard.index)
PCoA = skbio.stats.ordination.pcoa(DM_dist)
Now with sklearn's Multidimensional Scaling:
from sklearn.manifold import MDS
fig, ax=plt.subplots(ncols=5, figsize=(12,3))
for rs in range(5):
M = MDS(n_components=2, metric=True, random_state=rs, dissimilarity='precomputed')
A = M.fit(Ar_dist).embedding_
ax[rs].scatter(A[:,0],A[:,1], c=[{0:"b", 1:"g", 2:"r"}[t] for t in Se_targets])