What do all the distributions available in scipy.stats look like?

Question

Visualizing scipy.stats distributions

A histogram can be made of the scipy.stats normal random variable to see what the distribution looks like.

% matplotlib inline
import pandas as pd
import scipy.stats as stats
d = stats.norm()
rv = d.rvs(100000)
pd.Series(rv).hist(bins=32, normed=True)

What do the other distributions look like?

Whiplash

Answer 1

Visualizing all scipy.stats distributions

Based on the list of scipy.stats distributions, plotted below are the histograms and PDFs of each continuous random variable. The code used to generate each distribution is at the bottom. Note: The shape constants were taken from the examples on the scipy.stats distribution documentation pages.

alpha(a=3.57, loc=0.00, scale=1.00)

anglit(loc=0.00, scale=1.00)

arcsine(loc=0.00, scale=1.00)

beta(a=2.31, loc=0.00, scale=1.00, b=0.63)

betaprime(a=5.00, loc=0.00, scale=1.00, b=6.00)

bradford(loc=0.00, c=0.30, scale=1.00)

burr(loc=0.00, c=10.50, scale=1.00, d=4.30)

cauchy(loc=0.00, scale=1.00)

chi(df=78.00, loc=0.00, scale=1.00)

chi2(df=55.00, loc=0.00, scale=1.00)

cosine(loc=0.00, scale=1.00)

dgamma(a=1.10, loc=0.00, scale=1.00)

dweibull(loc=0.00, c=2.07, scale=1.00)

erlang(a=2.00, loc=0.00, scale=1.00)

expon(loc=0.00, scale=1.00)

exponnorm(loc=0.00, K=1.50, scale=1.00)

exponpow(loc=0.00, scale=1.00, b=2.70)

exponweib(a=2.89, loc=0.00, c=1.95, scale=1.00)

f(loc=0.00, dfn=29.00, scale=1.00, dfd=18.00)

fatiguelife(loc=0.00, c=29.00, scale=1.00)

fisk(loc=0.00, c=3.09, scale=1.00)

foldcauchy(loc=0.00, c=4.72, scale=1.00)

foldnorm(loc=0.00, c=1.95, scale=1.00)

frechet_l(loc=0.00, c=3.63, scale=1.00)

frechet_r(loc=0.00, c=1.89, scale=1.00)

gamma(a=1.99, loc=0.00, scale=1.00)

gausshyper(a=13.80, loc=0.00, c=2.51, scale=1.00, b=3.12, z=5.18)

genexpon(a=9.13, loc=0.00, c=3.28, scale=1.00, b=16.20)

genextreme(loc=0.00, c=-0.10, scale=1.00)

gengamma(a=4.42, loc=0.00, c=-3.12, scale=1.00)

genhalflogistic(loc=0.00, c=0.77, scale=1.00)

genlogistic(loc=0.00, c=0.41, scale=1.00)

gennorm(loc=0.00, beta=1.30, scale=1.00)

genpareto(loc=0.00, c=0.10, scale=1.00)

gilbrat(loc=0.00, scale=1.00)

gompertz(loc=0.00, c=0.95, scale=1.00)

gumbel_l(loc=0.00, scale=1.00)

gumbel_r(loc=0.00, scale=1.00)

halfcauchy(loc=0.00, scale=1.00)

halfgennorm(loc=0.00, beta=0.68, scale=1.00)

halflogistic(loc=0.00, scale=1.00)

halfnorm(loc=0.00, scale=1.00)

hypsecant(loc=0.00, scale=1.00)

invgamma(a=4.07, loc=0.00, scale=1.00)

invgauss(mu=0.14, loc=0.00, scale=1.00)

invweibull(loc=0.00, c=10.60, scale=1.00)

johnsonsb(a=4.32, loc=0.00, scale=1.00, b=3.18)

johnsonsu(a=2.55, loc=0.00, scale=1.00, b=2.25)

ksone(loc=0.00, scale=1.00, n=1000.00)

kstwobign(loc=0.00, scale=1.00)

laplace(loc=0.00, scale=1.00)

levy(loc=0.00, scale=1.00)

levy_l(loc=0.00, scale=1.00)

loggamma(loc=0.00, c=0.41, scale=1.00)

logistic(loc=0.00, scale=1.00)

loglaplace(loc=0.00, c=3.25, scale=1.00)

lognorm(loc=0.00, s=0.95, scale=1.00)

lomax(loc=0.00, c=1.88, scale=1.00)

maxwell(loc=0.00, scale=1.00)

mielke(loc=0.00, s=3.60, scale=1.00, k=10.40)

nakagami(loc=0.00, scale=1.00, nu=4.97)

ncf(loc=0.00, dfn=27.00, nc=0.42, dfd=27.00, scale=1.00)

nct(df=14.00, loc=0.00, scale=1.00, nc=0.24)

ncx2(df=21.00, loc=0.00, scale=1.00, nc=1.06)

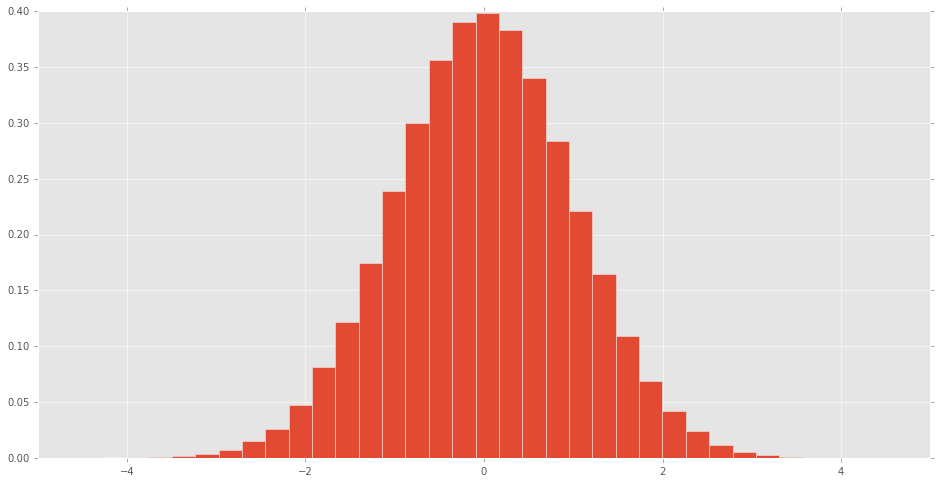
norm(loc=0.00, scale=1.00)

pareto(loc=0.00, scale=1.00, b=2.62)

pearson3(loc=0.00, skew=0.10, scale=1.00)

powerlaw(a=1.66, loc=0.00, scale=1.00)

powerlognorm(loc=0.00, s=0.45, scale=1.00, c=2.14)

powernorm(loc=0.00, c=4.45, scale=1.00)

rayleigh(loc=0.00, scale=1.00)

rdist(loc=0.00, c=0.90, scale=1.00)

recipinvgauss(mu=0.63, loc=0.00, scale=1.00)

reciprocal(a=0.01, loc=0.00, scale=1.00, b=1.01)

rice(loc=0.00, scale=1.00, b=0.78)

semicircular(loc=0.00, scale=1.00)

t(df=2.74, loc=0.00, scale=1.00)

triang(loc=0.00, c=0.16, scale=1.00)

truncexpon(loc=0.00, scale=1.00, b=4.69)

truncnorm(a=0.10, loc=0.00, scale=1.00, b=2.00)

tukeylambda(loc=0.00, scale=1.00, lam=3.13)

uniform(loc=0.00, scale=1.00)

vonmises(loc=0.00, scale=1.00, kappa=3.99)

vonmises_line(loc=0.00, scale=1.00, kappa=3.99)

wald(loc=0.00, scale=1.00)

weibull_max(loc=0.00, c=2.87, scale=1.00)

weibull_min(loc=0.00, c=1.79, scale=1.00)

wrapcauchy(loc=0.00, c=0.03, scale=1.00)

Generation Code

Here is the Jupyter Notebook used to generate the plots.

%matplotlib inline

import io
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib
import matplotlib.pyplot as plt

matplotlib.rcParams['figure.figsize'] = (16.0, 14.0)
matplotlib.style.use('ggplot')

---

# Distributions to check, shape constants were taken from the examples on the scipy.stats distribution documentation pages.
DISTRIBUTIONS = [
    stats.alpha(a=3.57, loc=0.0, scale=1.0), stats.anglit(loc=0.0, scale=1.0), 
    stats.arcsine(loc=0.0, scale=1.0), stats.beta(a=2.31, b=0.627, loc=0.0, scale=1.0), 
    stats.betaprime(a=5, b=6, loc=0.0, scale=1.0), stats.bradford(c=0.299, loc=0.0, scale=1.0),
    stats.burr(c=10.5, d=4.3, loc=0.0, scale=1.0), stats.cauchy(loc=0.0, scale=1.0), 
    stats.chi(df=78, loc=0.0, scale=1.0), stats.chi2(df=55, loc=0.0, scale=1.0),
    stats.cosine(loc=0.0, scale=1.0), stats.dgamma(a=1.1, loc=0.0, scale=1.0), 
    stats.dweibull(c=2.07, loc=0.0, scale=1.0), stats.erlang(a=2, loc=0.0, scale=1.0), 
    stats.expon(loc=0.0, scale=1.0), stats.exponnorm(K=1.5, loc=0.0, scale=1.0),
    stats.exponweib(a=2.89, c=1.95, loc=0.0, scale=1.0), stats.exponpow(b=2.7, loc=0.0, scale=1.0),
    stats.f(dfn=29, dfd=18, loc=0.0, scale=1.0), stats.fatiguelife(c=29, loc=0.0, scale=1.0), 
    stats.fisk(c=3.09, loc=0.0, scale=1.0), stats.foldcauchy(c=4.72, loc=0.0, scale=1.0),
    stats.foldnorm(c=1.95, loc=0.0, scale=1.0), stats.frechet_r(c=1.89, loc=0.0, scale=1.0),
    stats.frechet_l(c=3.63, loc=0.0, scale=1.0), stats.genlogistic(c=0.412, loc=0.0, scale=1.0),
    stats.genpareto(c=0.1, loc=0.0, scale=1.0), stats.gennorm(beta=1.3, loc=0.0, scale=1.0), 
    stats.genexpon(a=9.13, b=16.2, c=3.28, loc=0.0, scale=1.0), stats.genextreme(c=-0.1, loc=0.0, scale=1.0),
    stats.gausshyper(a=13.8, b=3.12, c=2.51, z=5.18, loc=0.0, scale=1.0), stats.gamma(a=1.99, loc=0.0, scale=1.0),
    stats.gengamma(a=4.42, c=-3.12, loc=0.0, scale=1.0), stats.genhalflogistic(c=0.773, loc=0.0, scale=1.0),
    stats.gilbrat(loc=0.0, scale=1.0), stats.gompertz(c=0.947, loc=0.0, scale=1.0),
    stats.gumbel_r(loc=0.0, scale=1.0), stats.gumbel_l(loc=0.0, scale=1.0),
    stats.halfcauchy(loc=0.0, scale=1.0), stats.halflogistic(loc=0.0, scale=1.0),
    stats.halfnorm(loc=0.0, scale=1.0), stats.halfgennorm(beta=0.675, loc=0.0, scale=1.0),
    stats.hypsecant(loc=0.0, scale=1.0), stats.invgamma(a=4.07, loc=0.0, scale=1.0),
    stats.invgauss(mu=0.145, loc=0.0, scale=1.0), stats.invweibull(c=10.6, loc=0.0, scale=1.0),
    stats.johnsonsb(a=4.32, b=3.18, loc=0.0, scale=1.0), stats.johnsonsu(a=2.55, b=2.25, loc=0.0, scale=1.0),
    stats.ksone(n=1e+03, loc=0.0, scale=1.0), stats.kstwobign(loc=0.0, scale=1.0),
    stats.laplace(loc=0.0, scale=1.0), stats.levy(loc=0.0, scale=1.0),
    stats.levy_l(loc=0.0, scale=1.0), stats.levy_stable(alpha=0.357, beta=-0.675, loc=0.0, scale=1.0),
    stats.logistic(loc=0.0, scale=1.0), stats.loggamma(c=0.414, loc=0.0, scale=1.0),
    stats.loglaplace(c=3.25, loc=0.0, scale=1.0), stats.lognorm(s=0.954, loc=0.0, scale=1.0),
    stats.lomax(c=1.88, loc=0.0, scale=1.0), stats.maxwell(loc=0.0, scale=1.0),
    stats.mielke(k=10.4, s=3.6, loc=0.0, scale=1.0), stats.nakagami(nu=4.97, loc=0.0, scale=1.0),
    stats.ncx2(df=21, nc=1.06, loc=0.0, scale=1.0), stats.ncf(dfn=27, dfd=27, nc=0.416, loc=0.0, scale=1.0),
    stats.nct(df=14, nc=0.24, loc=0.0, scale=1.0), stats.norm(loc=0.0, scale=1.0),
    stats.pareto(b=2.62, loc=0.0, scale=1.0), stats.pearson3(skew=0.1, loc=0.0, scale=1.0),
    stats.powerlaw(a=1.66, loc=0.0, scale=1.0), stats.powerlognorm(c=2.14, s=0.446, loc=0.0, scale=1.0),
    stats.powernorm(c=4.45, loc=0.0, scale=1.0), stats.rdist(c=0.9, loc=0.0, scale=1.0),
    stats.reciprocal(a=0.00623, b=1.01, loc=0.0, scale=1.0), stats.rayleigh(loc=0.0, scale=1.0),
    stats.rice(b=0.775, loc=0.0, scale=1.0), stats.recipinvgauss(mu=0.63, loc=0.0, scale=1.0),
    stats.semicircular(loc=0.0, scale=1.0), stats.t(df=2.74, loc=0.0, scale=1.0),
    stats.triang(c=0.158, loc=0.0, scale=1.0), stats.truncexpon(b=4.69, loc=0.0, scale=1.0),
    stats.truncnorm(a=0.1, b=2, loc=0.0, scale=1.0), stats.tukeylambda(lam=3.13, loc=0.0, scale=1.0),
    stats.uniform(loc=0.0, scale=1.0), stats.vonmises(kappa=3.99, loc=0.0, scale=1.0),
    stats.vonmises_line(kappa=3.99, loc=0.0, scale=1.0), stats.wald(loc=0.0, scale=1.0),
    stats.weibull_min(c=1.79, loc=0.0, scale=1.0), stats.weibull_max(c=2.87, loc=0.0, scale=1.0),
    stats.wrapcauchy(c=0.0311, loc=0.0, scale=1.0)
]

---

bins = 32
size = 16384
plotData = []
for distribution in DISTRIBUTIONS:
    try:  
        # Create random data
        rv = pd.Series(distribution.rvs(size=size))
        # Get sane start and end points of distribution
        start = distribution.ppf(0.01)
        end = distribution.ppf(0.99)

        # Build PDF and turn into pandas Series
        x = np.linspace(start, end, size)
        y = distribution.pdf(x)
        pdf = pd.Series(y, x)

        # Get histogram of random data
        b = np.linspace(start, end, bins+1)
        y, x = np.histogram(rv, bins=b, normed=True)
        x = [(a+x[i+1])/2.0 for i,a in enumerate(x[0:-1])]
        hist = pd.Series(y, x)

        # Create distribution name and parameter string
        title = '{}({})'.format(distribution.dist.name, ', '.join(['{}={:0.2f}'.format(k,v) for k,v in distribution.kwds.items()]))

        # Store data for later
        plotData.append({
            'pdf': pdf,
            'hist': hist,
            'title': title
        })

    except Exception:
        print 'could not create data', distribution.dist.name

---

plotMax = len(plotData)

for i, data in enumerate(plotData):
    w = abs(abs(data['hist'].index[0]) - abs(data['hist'].index[1]))

    # Display
    plt.figure(figsize=(10, 6))
    ax = data['pdf'].plot(kind='line', label='Model PDF', legend=True, lw=2)
    ax.bar(data['hist'].index, data['hist'].values, label='Random Sample', width=w, align='center', alpha=0.5)
    ax.set_title(data['title'])

    # Grab figure
    fig = matplotlib.pyplot.gcf()
    # Output 'file'
    fig.savefig('~/Desktop/dist/'+data['title']+'.png', format='png', bbox_inches='tight')
    matplotlib.pyplot.close()

Whiplash

Went above and beyond for this answer! – Noonan

@Noonan Thanks, all the linking and images just involved a lot of your name, lol. – Whiplash

It's cool! This is the most comprehensive one I have ever seen. – Acetous

@Whiplash Thank you for all this code. This really helps me understand the continuous distributions. I was wondering -- as a follow-up from another answer you gave -- do you know how we can test for a best fit of discrete distributions in scipy.stats such as binom or poisson in your solution here? (#6620971)? – Somme

Someone give this dude a medal! – Tobias

Answer 2

Visualizing all scipy probability distributions in a single figure

Here is a solution that displays all the scipy probability distributions in a single figure and avoids the need to copy-paste (or web scrape) the distribution shape parameters by extracting them instead from the _distr_params file that contains sane parameters for all the available distributions.

Similarly to the accepted answer, a sample of random variates is generated for each distribution. These samples are then stored in a pandas dataframe where the columns containing identical distribution names are renamed (based on this answer by MaxU) because some distributions are listed more than once with different parameter definitions (e.g. kappa4). This way, the samples can be plotted using the convenient df.hist function which creates a grid of histograms. These plots are then overlaid with a line plot representing the probability density function ranging from the 0.1% quantile up to the 99.9% quantile.

There are a few additional things to point out:

• The location and scale parameters are set at the default values (0 and 1) for all the distributions.
• Some histograms show only a few very wide bars because of one or more outliers that are located outside of the 0.1-99.9% quantile limits.
• The plot width is limited to only 10 inches in this example so as to preserve the sharpness of the uploaded image. Because of this, you may notice that a few of the x labels (used as subtitles) overlap.
• There is no need to import matplotlib.pyplot seeing as the matplotlib objects are generated with the pandas plotting functions (unless you need plt.show).

The code for generating the x labels and the random variables is based on the accepted answer by tmthydvnprt and this answer by Adam Erickson in addition to the scipy documentation.

import numpy as np         # v 1.19.2
from scipy import stats    # v 1.5.2
import pandas as pd        # v 1.1.3

pd.options.display.max_columns = 6
np.random.seed(123)

size = 10000
names, xlabels, frozen_rvs, samples = [], [], [], []

# Extract names and sane parameters of all scipy probability distributions
# (except the deprecated ones) and loop through them to create lists of names,
# frozen random variables, samples of random variates and x labels
for name, params in stats._distr_params.distcont:
    if name not in ['frechet_l', 'frechet_r']:
        loc, scale = 0, 1
        names.append(name)
        params = list(params) + [loc, scale]
        
        # Create instance of random variable
        dist = getattr(stats, name)
        
        # Create frozen random variable using parameters and add it to the list
        # to be used to draw the probability density functions
        rv = dist(*params)
        frozen_rvs.append(rv)
        
        # Create sample of random variates
        samples.append(rv.rvs(size=size))
        
        # Create x label containing the distribution parameters
        p_names = ['loc', 'scale']
        if dist.shapes:
            p_names = [sh.strip() for sh in dist.shapes.split(',')] + ['loc', 'scale']
        xlabels.append(', '.join([f'{pn}={pv:.2f}' for pn, pv in zip(p_names, params)]))

# Create pandas dataframe containing all the samples
df = pd.DataFrame(data=np.array(samples).T, columns=[name for name in names])
# Rename the duplicate column names by adding a period and an integer at the end
df.columns = pd.io.parsers.ParserBase({'names':df.columns})._maybe_dedup_names(df.columns)

df.head()

#       alpha     anglit    arcsine  ...  weibull_max  weibull_min   wrapcauchy
# 0  0.327165   0.166185   0.018339  ...    -0.928914     0.359808     4.454122
# 1  0.241819   0.373590   0.630670  ...    -0.733157     0.479574     2.778336
# 2  0.231489   0.352024   0.457251  ...    -0.580317     1.312468     4.932825
# 3  0.290551  -0.133986   0.797215  ...    -0.954856     0.341515     3.874536
# 4  0.334494  -0.353015   0.439837  ...    -1.440794     0.498514     5.195171

# Set parameters for figure dimensions
nplot = df.columns.size
cols = 3
rows = int(np.ceil(nplot/cols))
subp_w = 10/cols  # 10 corresponds to the figure width in inches
subp_h = 0.9*subp_w

# Create pandas grid of histograms
axs = df.hist(density=True, bins=15, grid=False, edgecolor='w',
              linewidth=0.5, legend=False,
              layout=(rows, cols), figsize=(cols*subp_w, rows*subp_h))

# Loop over subplots to draw probability density function and apply some
# additional formatting
for idx, ax in enumerate(axs.flat[:df.columns.size]):
    rv = frozen_rvs[idx]
    x = np.linspace(rv.ppf(0.001), rv.ppf(0.999), size)
    ax.plot(x, rv.pdf(x), c='black', alpha=0.5)
    ax.set_title(ax.get_title(), pad=25)
    ax.set_xlim(x.min(), x.max())
    ax.set_xlabel(xlabels[idx], fontsize=8, labelpad=10)
    ax.xaxis.set_label_position('top')
    ax.tick_params(axis='both', labelsize=9)
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)

ax.figure.subplots_adjust(hspace=0.8, wspace=0.3)

Droit