How do I find the surface between lines based on intercept and slope which includes the origin?

Question

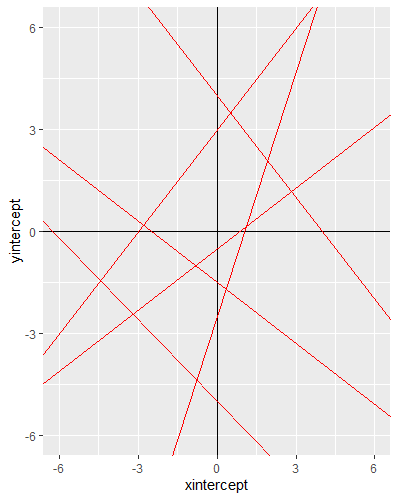
I'm looking for a way to visualize the surface between a number of straight lines, which are defined in a dataframe through their intercepts and slopes. The surface I am looking for is the one that encloses the origin (0, 0).

The number of lines may vary (even though in the following simplified example I only have 6), and some of them may be redundant (i.e. they do not enclose the surface I am looking for because other lines are more constraining).

Let's take this simple dataframe:

df <- data.frame("Line" = c("A", "B", "C", "D", "E", "F"),
                 "Intercept" = c(4, 3, -2.5, -1.5, -5, -.5),
                 "Slope" = c(-1, 1, 2.4, -.6, -.8, .6))

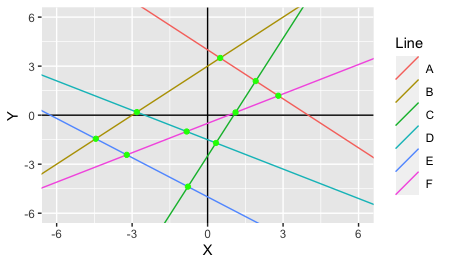
Plotting these lines with ggplot2:

ggplot(data = df) +
  geom_vline(xintercept = 0) +
  geom_hline(yintercept = 0) +
  geom_abline(mapping = aes(intercept = Intercept, slope = Slope),
              colour = "red") +
  coord_cartesian(xlim = c(-6, 6), ylim = c(-6, 6))

Gives me the following output:

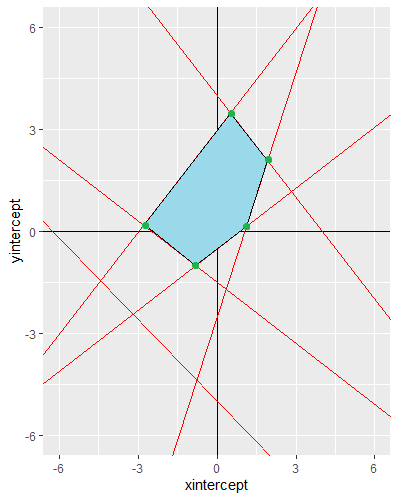
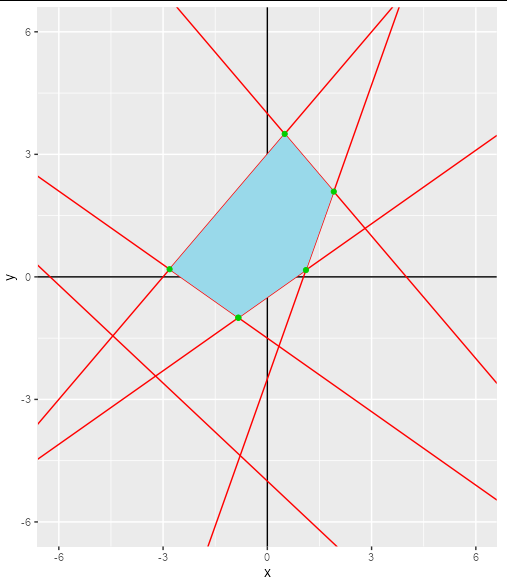
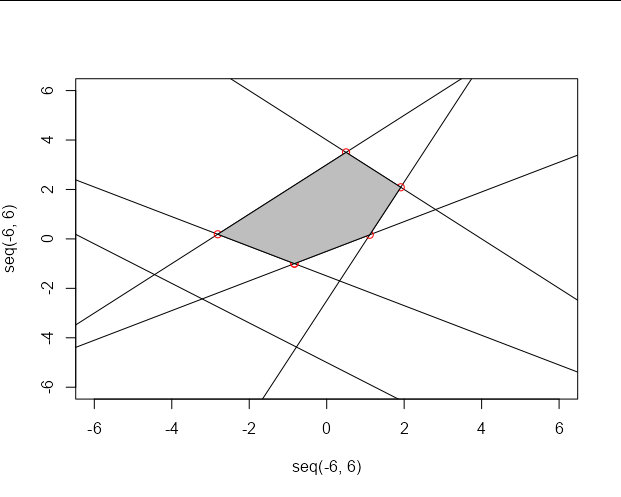
Basically I want to find intersections between the lines that enclose the origin (0, 0), disregarding the redundant one (the bottom left in this case, with intercept = -5 and slope = -0.8). Those 5 intersection points would then be used to plot the convex hull.

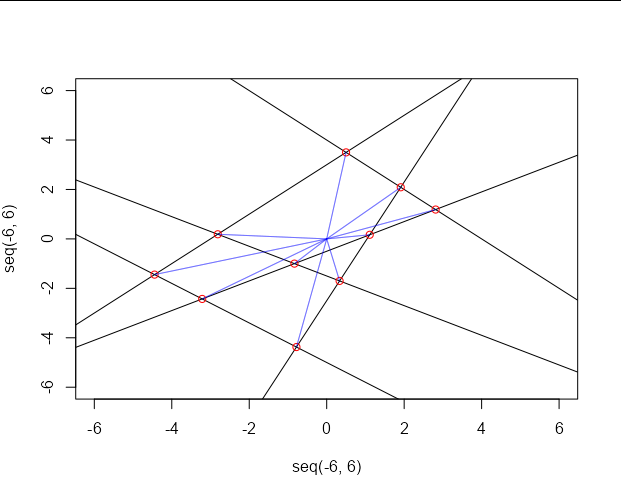
My main problem lies in finding the intersection points of the constraining lines (green points below) in order to be able to find the blue surface.

QUESTION: Any suggestions on how to deal with this in R, ideally in a way that can be extended to larger dataframes (including more constraining and redundant lines)?

ADDITIONAL QUESTION: geom_abline() does not have a group aesthetic similar to geom_line(), which could be used to identify the line. Does anyone know a workaround to draw straight lines in ggplot2 based on slopes and intercepts (or two user-defined points of the line)?

Thanks in advance for any suggestions or (parts of) potential solutions!

UPDATE: In order to center the polygon around point (a,b) instead of the origin (0, 0), I have amended the original code (in particular the ìnnermost()`-function from @AllanCameron as follows:

innermost <- function(slopes, intercepts, a, b) {

  meetings <- function(slopes, intercepts) {
    meets_at <- function(i1, s1, i2, s2) {
      ifelse(s1 - s2 == 0, NA, (i2 - i1)/(s1 - s2))
    }
    xvals <- outer(seq_along(slopes), seq_along(slopes), function(i, j) {
      meets_at(intercepts[i], slopes[i], intercepts[j], slopes[j])
    })

    yvals <- outer(seq_along(slopes), seq_along(slopes), function(i, j) {
      intercepts + slopes *
        meets_at(intercepts[i], slopes[i], intercepts[j], slopes[j])
    })

    cbind(x = xvals[lower.tri(xvals)], y = yvals[lower.tri(yvals)])

  }

  xy <- meetings(slopes, intercepts)
  xy[,1] <- xy[,1] - a
  xy[,2] <- xy[,2] - b

  is_cut <- function(x, y, slopes, intercepts, a, b) {
    d <- sqrt(x^2 + y^2)
    slope <- y / x
    xvals <- (intercepts + slopes*a - b) / (slope - slopes)
    yvals <- xvals * slopes + (intercepts + slopes*a - b)
    ds <- sqrt(xvals^2 + yvals^2)
    any(d - ds > 1e-6 & sign(xvals) == sign(x) & sign(yvals) == sign(y))
  }

  xy <- xy[sapply(seq(nrow(xy)), function(i) {
    !is_cut(xy[i, 1], xy[i, 2], slopes, intercepts, a, b)
  }),]

  xy <- xy[order(atan2(xy[,2], xy[,1])),]
  
  xy[,1] <- xy[,1] + a
  xy[,2] <- xy[,2] + b
  
  as.data.frame(rbind(xy, xy[1,]))
}

Alarm

I think I would try to use the sf package for this. – Myoglobin

You have defined a pentangle that surrounds the origin. But the triangle defined by the lowest three vertices of your pentangle also includes the origin and is clearly smaller than the pentangle. What makes the pentangle preferable to the triangle? – Aimee

@Limey: the top segment of the triangle is not part of one of the constraining lines. Basically, each side of the blue polygon should overlap with one of the red lines, or in other words the two vertices on each end of the side should be on the same red line. Does that help? – Alarm

Yes it does. I'm about to post a partial solution... – Aimee

Answer 1

Here's a solution that only requires a bit of geometry and algebra, using only base R. We can define a function, innermost that finds the x, y co-ordinates of the inner polygon and returns them in counter-clockwise order as a data frame. This allows you to create your ggplot by doing:

ggplot(data = df) +
  geom_vline(xintercept = 0) +
  geom_hline(yintercept = 0) +
  geom_abline(mapping = aes(intercept = Intercept, slope = Slope),
              colour = "red") +
  geom_polygon(data = innermost(df$Slope, df$Intercept), aes(x, y),
               fill = "#99d9ea") +
  geom_point(data = innermost(df$Slope, df$Intercept), aes(x, y), 
             color = 'green3') +
  coord_cartesian(xlim = c(-6, 6), ylim = c(-6, 6))

The function innermost is defined as follows:

innermost <- function(slopes, intercepts) {
  
  meetings <- function(slopes, intercepts) {
    meets_at <- function(i1, s1, i2, s2) {
      ifelse(s1 - s2 == 0, NA, (i2 - i1)/(s1 - s2))
    }    
    xvals <- outer(seq_along(slopes), seq_along(slopes), function(i, j) {
      meets_at(intercepts[i], slopes[i], intercepts[j], slopes[j])
    })
    
    yvals <- outer(seq_along(slopes), seq_along(slopes), function(i, j) {
      intercepts + slopes *
        meets_at(intercepts[i], slopes[i], intercepts[j], slopes[j])
    })
    
    cbind(x = xvals[lower.tri(xvals)], y = yvals[lower.tri(yvals)])
    
  xy <- meetings(slopes, intercepts)
  is_cut <- function(x, y, slopes, intercepts) {
    d <- sqrt(x^2 + y^2)
    slope <- y / x
    xvals <- intercepts / (slope - slopes)
    yvals <- xvals * slopes + intercepts
    ds <- sqrt(xvals^2 + yvals^2)
    any(d - ds > 1e-6 & sign(xvals) == sign(x) & sign(yvals) == sign(y))
  }
  xy <- xy[sapply(seq(nrow(xy)), function(i) {
    !is_cut(xy[i, 1], xy[i, 2], slopes, intercepts)
  }),]
  xy <- xy[order(atan2(xy[,2], xy[,1])),]
  as.data.frame(rbind(xy, xy[1,]))
}

---

Explanation

Firstly, it's straightforward to get the intersection of two straight lines. The formula of a straight line is given by , where m is the slope and c is the intercept. So if we have two different straight lines given by the equations and then they must meet where

Rearranging this we get

or

which means the lines meet where

That is, if we have intercept1 and slope1 for the first line and intercept2 and slope2 for the second, then we can find the x value of the meeting point with this simple function:

meets_at <- function(intercept1, slope1, intercept2, slope2) {
  ifelse(slope1 - slope2 == 0, NA, (intercept2 - intercept1)/(slope1 - slope2))
}

Note that if the lines are parallel, i.e. slope1 - slope2 == 0, they will not have a unique meeting point and this function should return NA

We can use this function across all pairs of lines to get all the intersections by using outer:

meetings <- function(slopes, intercepts) {
  
  xvals <- outer(seq_along(slopes), seq_along(slopes), function(i, j) {
            meets_at(intercepts[i], slopes[i], intercepts[j], slopes[j])
           })
  
  yvals <- outer(seq_along(slopes), seq_along(slopes), function(i, j) {
            intercepts + slopes *
            meets_at(intercepts[i], slopes[i], intercepts[j], slopes[j])
          })
  
  cbind(x = xvals[lower.tri(xvals)], y = yvals[lower.tri(yvals)])
}

For example, if we plot these points we will see we get all the intersections of the lines plotted:

plot(seq(-6, 6), seq(-6, 6), type = 'n')
for(i in seq(nrow(df))) abline(a = df$Intercept[i], b = df$Slope[i])
xy <- meetings(df$Slope, df$Intercept)
points(xy[,1], xy[,2], col = 'red')

This still leaves us the problem of finding only the innermost points that form the outline of your desired polygon. To do this, note what happens when we draw a line from the origin (0, 0) to each of the intersection points in the image above:

xy <- xy[abs(xy[,1]) < 6 & abs(xy[,2] < 6),] # Remove intersections outside plot

for(i in seq(nrow(df))) {
  segments(x0 = 0, y0 = 0, x1 = xy[,1], y1 = xy[,2], col = '#0000ff20')
}

Note that the blue lines going from the origin to the innermost vertices (which are the ones we want to keep) are not crossed by any other lines. In other words, the vertices we want to discard are those from which you cannot draw a straight line to the origin without it being intersected by another line.

We can therefore work out if there are any lines crossing the segments joining the origin to the intersections, and keep only those that are not crossed.

We also need to arrange the final points in circumferential order. This is done by calculating the arctangent of the angle between the x axis and a line drawn to the point, which is just atan2(y, x). This gives us a number between -pi and pi, with which the points can be ordered counter clockwise starting from the 9 o-clock position:

innermost <- function(slopes, intercepts) {
  xy <- meetings(slopes, intercepts)
  is_cut <- function(x, y, slopes, intercepts) {
    d <- sqrt(x^2 + y^2)
    slope <- y / x
    xvals <- intercepts / (slope - slopes)
    yvals <- xvals * slopes + intercepts
    ds <- sqrt(xvals^2 + yvals^2)
    any(d - ds > 1e-6 & sign(xvals) == sign(x) & sign(yvals) == sign(y))
  }
  xy <- xy[sapply(seq(nrow(xy)), function(i) {
    !is_cut(xy[i, 1], xy[i, 2], slopes, intercepts)
  }),]
  xy <- xy[order(atan2(xy[,2], xy[,1])),]
  as.data.frame(rbind(xy, xy[1,]))
}

We can use the above function to find the innermost polygon created by a group of lines. Plotting in base R, we can do:

plot(seq(-6, 6), seq(-6, 6), type = 'n')
for(i in seq(nrow(df))) abline(a = df$Intercept[i], b = df$Slope[i])
xy <- innermost(df$Slope, df$Intercept)
points(xy$x, xy$y, col = 'red')
polygon(xy$x, xy$y, col = 'gray')

Steelwork

This is an impressive answer. Wow – Purdy

Wow yes. This is exactly what I need. Love that you managed to do this in base R, and it's easily extendable to larger datasets. Beautifully logical, thank you so much! – Alarm

Hi Allan, could you perhaps help me? I'm trying to amend the function to calculate the innermost polygon around a point (a,b) instead of around the origin. I know I need to modify the is_cut function (calculate distance d to (a,b) instead of (0, 0) and update the slope, xvals and yvals, calculate ds to (a,b)) and include the point in the function call to define xy. Finally the atan2 function needs to be modified as well. However, I cannot figure out how to do this, as somehow I keep getting wrong results. Could you give a hint if I have forgotten something? – Alarm

@Alarm isn't the solution to subtract (a, b) from each point and add it on again at the end? – Steelwork

@AllanCameron I don't think so. In the example, if you apply the innermost function to calculate the polygon around the origin, you get a pentagon (shown in your reply). Let's say I want to calculate the polygon around the point (2, 1) instead of (0, 0), the polygon is a rectangle, so innermost should select different intersection points between the diagonals. – Alarm

Oh no I see your point. Shifting all intersection points from the meetings() function with (a,b) and then applying the is_cut() and adding back (a,b) afterwards. I'll try that! – Alarm

@Alarm exactly. – Steelwork

@AllanCameron it took me a while but I found it: needed to change the xvals and yvals in the is_cut function as well, as you don't only need to change the points in xy, but also the intersections with the diagonal lines (to check if and where the segments through origin & intersections cross existing lines). I have updated the entire answer. Thanks a lot for your hints, it's been very valuable! – Alarm

Answer 2

Partial solution

By using the combn function, it's a matter of simple algebra to find all the intersections of the lines:

intersections <- as_tibble(
                   t(combn(df$Line, 2)), 
                   .name_repair=\(x) c("Line1", "Line2")
                 ) %>% 
                 left_join(
                   df %>% rename(Intercept1=Intercept, Slope1=Slope),
                   by=c("Line1"="Line")
                 ) %>% 
                 left_join(
                   df %>% rename(Intercept2=Intercept, Slope2=Slope),
                   by=c("Line2"="Line")
                 ) %>% 
                 mutate(
                   X=(Intercept2 - Intercept1)/(Slope1 - Slope2),
                   Y=Slope1 * X + Intercept1,
                   Row=row_number()
                 ) %>%
                 select(-starts_with("I"), -starts_with("S"))
> intersections
# A tibble: 15 × 5
   Line1 Line2       X       Y   Row
   <chr> <chr>   <dbl>   <dbl> <int>
 1 A     B       0.5     3.5       1
 2 A     C       1.91    2.09      2
 3 A     D      13.8    -9.75      3
 4 A     E      45     -41         4
 5 A     F       2.81    1.19      5
 6 B     C       3.93    6.93      6
 7 B     D      -2.81    0.188     7
 8 B     E      -4.44   -1.44      8
 9 B     F      -8.75   -5.75      9
10 C     D       0.333  -1.7      10
11 C     E      -0.781  -4.38     11
12 C     F       1.11    0.167    12
13 D     E     -17.5     9.00     13
14 D     F      -0.833  -1        14
15 E     F      -3.21   -2.43     15

And check that we've correctly identified the intersections

intersections %>% 
  ggplot() +
    geom_vline(xintercept = 0) +
    geom_hline(yintercept = 0) +
    geom_abline(data=df, mapping = aes(intercept = Intercept, slope = Slope, colour = Line)) +
    geom_point(aes(x=X, y=Y), colour="green") +
    coord_cartesian(xlim = c(-6, 6), ylim = c(-6, 6))

Now we could use combn again to generate all possible combinations of these points of intersection points and use chull to obtain the convext hull of each and proceed from there, but that's not efficient.

As @Roland suggests, the sf package is probably the way to go from here, but I'm not very familiar with it. From here on in, I'm thinking out loud...

We can get the convex hulls of all sets of subsets of these points of size m (with m > 3 for obvious reasons) with

library(sf)

getPolygons <- function(data, m=3) { 
  pointSets <- as_tibble(
                 t(combn(1:nrow(intersections), m=m)), 
                 .name_repair=\(x) as.character(1:length(x))
               ) %>% 
               mutate(Polygon=row_number()) %>% 
               pivot_longer(
                 -Polygon, 
                 names_to="index", 
                 values_to="Row"
               ) %>% 
               select(-index)
    pointSets %>% 
      group_by(Polygon) %>% 
      group_map(
        function(.x, .y) {
          z <- .x %>% left_join(data, by="Row") %>% select(X, Y)
          st_convex_hull(st_multipoint(as.matrix(z)))
        }
    ) 
allPolygons <- intersections %>% getPolygons(3)

And then check if the convex hull contains the origin (and calculate the area of those convex hulls that do) with

areasOfPolygonsAroundOrigin <- 
  sapply(
    allPolygons,
    function(x) {
      if(!is_empty(st_contains(x, st_point(c(0, 0)))[[1]])) {
        st_area(x) 
      } else {
        Inf
      }
    }
  )

which.min(areasOfPolygonsAroundOrigin)
[1] 311
areasOfPolygonsAroundOrigin[which.min(areasOfPolygonsAroundOrigin)]
[1] 1.465085

If the smallest area is infinite, then there are no such convex hulls that include the origin, so we step up to the set of convex hulls that contain one more of the points of intersection.

The missing part of the logic is to identify which of the convex hulls are defined by segments of the input lines that connect points of intersection. That's what I've not been able to do. sf_linestring may be helpful here.

Aimee

Thank you so much, that's already very helpful! I can easily extend the answer on the intersections to larger datasets (which is a bit more complex than the simplified example). I definitely will check out the sf package, I wasn't aware of its existence but it seems to hold the answer - probably a bit of a learning curve though. I'll get back if I manage to find the last piece of the puzzle. – Alarm