I tried to write code to solve the standard Integer Partition problem (Wikipedia). The code I wrote was a mess. I need an elegant solution to solve the problem, because I want to improve my coding style. This is not a homework question.
Elegant Python code for Integer Partitioning [closed]
You might get a more useful answer by posting your original code on codereview.stackexchange. –
Paltry
The term 'elegant' is subjective. What some may find elegant, others won't. So don't be surprised if another programmer does not find your code 'elegant'. If it works and is maintainable, it's good enough. –
Havildar
While this answer is fine, I'd recommend skovorodkin's answer.
>>> def partition(number):
... answer = set()
... answer.add((number, ))
... for x in range(1, number):
... for y in partition(number - x):
... answer.add(tuple(sorted((x, ) + y)))
... return answer
...
>>> partition(4)
set([(1, 3), (2, 2), (1, 1, 2), (1, 1, 1, 1), (4,)])
If you want all permutations(ie (1, 3) and (3, 1)) change answer.add(tuple(sorted((x, ) + y)) to answer.add((x, ) + y)
Be warned that while somewhat elegant, this algorithm is extremely slow compared to efficient algorithms like this one, which sadly sacrificies elegance and readability for speed. My timings show it to be 46 times faster for number=10, 450 times faster for number=15 and 5500 times faster for number=22. At this point your algorithm used 8 seconds to complete, compared to 0.0014 seconds for the efficient version. –
Fourposter
@LauritzV.Thaulow that link redirects to a 404, I think this is the new URL: jeromekelleher.net/generating-integer-partitions.html –
Martinmas
A smaller and faster than Nolen's function:
def partitions(n, I=1):
yield (n,)
for i in range(I, n//2 + 1):
for p in partitions(n-i, i):
yield (i,) + p
Let's compare them:
In [10]: %timeit -n 10 r0 = nolen(20)
1.37 s ± 28.7 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
In [11]: %timeit -n 10 r1 = list(partitions(20))
979 µs ± 82.9 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
In [13]: sorted(map(sorted, r0)) == sorted(map(sorted, r1))
Out[14]: True
Looks like it's 1370 times faster for n = 20.
Anyway, it's still far from accel_asc:
def accel_asc(n):
a = [0 for i in range(n + 1)]
k = 1
y = n - 1
while k != 0:
x = a[k - 1] + 1
k -= 1
while 2 * x <= y:
a[k] = x
y -= x
k += 1
l = k + 1
while x <= y:
a[k] = x
a[l] = y
yield a[:k + 2]
x += 1
y -= 1
a[k] = x + y
y = x + y - 1
yield a[:k + 1]
Mine is not only slower, but requires much more memory (but apparently is much easier to remember):
In [18]: %timeit -n 5 r2 = list(accel_asc(50))
114 ms ± 1.04 ms per loop (mean ± std. dev. of 7 runs, 5 loops each)
In [19]: %timeit -n 5 r3 = list(partitions(50))
527 ms ± 8.86 ms per loop (mean ± std. dev. of 7 runs, 5 loops each)
In [24]: sorted(map(sorted, r2)) == sorted(map(sorted, r3))
Out[24]: True
You can find other versions on ActiveState: Generator For Integer Partitions (Python Recipe).
I use Python 3.6.1 and IPython 6.0.0.
Heh, this should very clearly be the accepted answer over mine. –
Unsearchable
I know this is a long shot but I have 2 questions regarding this answer: Does it account for the permutations of the partitions? And where should I input the number I want to be partitioned (ex: 5)? –
Kohn
@DGMS89, IIUYC, permutations are not included. I suppose
[*itertools.chain.from_iterable(set(itertools.permutations(p)) for p in partitions(5))] gives you what you need for n=5 with permutations. –
Ronrona @Ronrona Thanks for the help. So I just add that line after the code in your answer? –
Kohn
@DGMS89, check this out gist.github.com/skovorodkin/3f6678d64397523cd1b05779b666d726. Please note, that
accel_asc is more performant, so if you want to use that code in production, you'd better use accel_asc rather than my partitions function. –
Ronrona @Ronrona Many thanks. In fact I just need to understand the process your code does and use it once for some integers below 90. –
Kohn
One liner...see it to believe it p=lambda n,I=1: itertools.chain(((n,),), ((i,)+x for i in range(I,n//2+1) for x in p(n-i,i))); list(p(5)) –
Intertwist
While this answer is fine, I'd recommend skovorodkin's answer.
>>> def partition(number):
... answer = set()
... answer.add((number, ))
... for x in range(1, number):
... for y in partition(number - x):
... answer.add(tuple(sorted((x, ) + y)))
... return answer
...
>>> partition(4)
set([(1, 3), (2, 2), (1, 1, 2), (1, 1, 1, 1), (4,)])
If you want all permutations(ie (1, 3) and (3, 1)) change answer.add(tuple(sorted((x, ) + y)) to answer.add((x, ) + y)
Be warned that while somewhat elegant, this algorithm is extremely slow compared to efficient algorithms like this one, which sadly sacrificies elegance and readability for speed. My timings show it to be 46 times faster for number=10, 450 times faster for number=15 and 5500 times faster for number=22. At this point your algorithm used 8 seconds to complete, compared to 0.0014 seconds for the efficient version. –
Fourposter
@LauritzV.Thaulow that link redirects to a 404, I think this is the new URL: jeromekelleher.net/generating-integer-partitions.html –
Martinmas
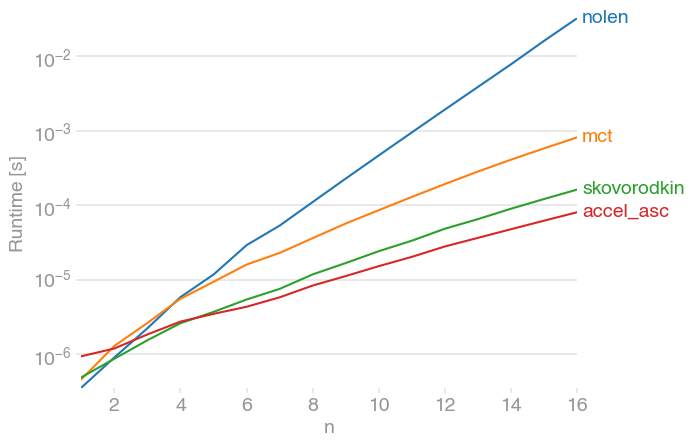
I've compared the solution with perfplot (a little project of mine for such purposes) and found that Nolen's top-voted answer is also the slowest.
Both answers supplied by skovorodkin are much faster. (Note the log-scale.)
To to generate the plot:
import perfplot
import collections
def nolen(number):
answer = set()
answer.add((number,))
for x in range(1, number):
for y in nolen(number - x):
answer.add(tuple(sorted((x,) + y)))
return answer
def skovorodkin(n):
return set(skovorodkin_yield(n))
def skovorodkin_yield(n, I=1):
yield (n,)
for i in range(I, n // 2 + 1):
for p in skovorodkin_yield(n - i, i):
yield (i,) + p
def accel_asc(n):
return set(accel_asc_yield(n))
def accel_asc_yield(n):
a = [0 for i in range(n + 1)]
k = 1
y = n - 1
while k != 0:
x = a[k - 1] + 1
k -= 1
while 2 * x <= y:
a[k] = x
y -= x
k += 1
l = k + 1
while x <= y:
a[k] = x
a[l] = y
yield tuple(a[: k + 2])
x += 1
y -= 1
a[k] = x + y
y = x + y - 1
yield tuple(a[: k + 1])
def mct(n):
partitions_of = []
partitions_of.append([()])
partitions_of.append([(1,)])
for num in range(2, n + 1):
ptitions = set()
for i in range(num):
for partition in partitions_of[i]:
ptitions.add(tuple(sorted((num - i,) + partition)))
partitions_of.append(list(ptitions))
return partitions_of[n]
perfplot.show(
setup=lambda n: n,
kernels=[nolen, mct, skovorodkin, accel_asc],
n_range=range(1, 17),
logy=True,
# https://mcmap.net/q/93625/-how-to-efficiently-compare-two-unordered-lists-not-sets
equality_check=lambda a, b: collections.Counter(set(a))
== collections.Counter(set(b)),
xlabel="n",
)
I needed to solve a similar problem, namely the partition of an integer n into d nonnegative parts, with permutations. For this, there's a simple recursive solution (see here):
def partition(n, d, depth=0):
if d == depth:
return [[]]
return [
item + [i]
for i in range(n+1)
for item in partition(n-i, d, depth=depth+1)
]
# extend with n-sum(entries)
n = 5
d = 3
lst = [[n-sum(p)] + p for p in partition(n, d-1)]
print(lst)
Output:
[
[5, 0, 0], [4, 1, 0], [3, 2, 0], [2, 3, 0], [1, 4, 0],
[0, 5, 0], [4, 0, 1], [3, 1, 1], [2, 2, 1], [1, 3, 1],
[0, 4, 1], [3, 0, 2], [2, 1, 2], [1, 2, 2], [0, 3, 2],
[2, 0, 3], [1, 1, 3], [0, 2, 3], [1, 0, 4], [0, 1, 4],
[0, 0, 5]
]
A related task (where
nonnegative is replaced by positive) is relevant to Nonogram puzzles. May I ask what that was for? –
Piliferous @Piliferous This was for creating multivariate polynomials of a particular order, e.g.,
x^3 y^1 z^4, x^8 y^0 z^0 etc. (The sum of the exponents is always n). –
Responser Much quicker than the accepted response and not bad looking, either. The accepted response does lots of the same work multiple times because it calculates the partitions for lower integers multiple times. For example, when n=22 the difference is 12.7 seconds against 0.0467 seconds.
def partitions_dp(n):
partitions_of = []
partitions_of.append([()])
partitions_of.append([(1,)])
for num in range(2, n+1):
ptitions = set()
for i in range(num):
for partition in partitions_of[i]:
ptitions.add(tuple(sorted((num - i, ) + partition)))
partitions_of.append(list(ptitions))
return partitions_of[n]
The code is essentially the same except we save the partitions of smaller integers so we don't have to calculate them again and again.
I'm a bit late to the game, but I can offer a contribution which might qualify as more elegant in a few senses:
def partitions(n, m = None):
"""Partition n with a maximum part size of m. Yield non-increasing
lists in decreasing lexicographic order. The default for m is
effectively n, so the second argument is not needed to create the
generator unless you do want to limit part sizes.
"""
if m is None or m >= n: yield [n]
for f in range(n-1 if (m is None or m >= n) else m, 0, -1):
for p in partitions(n-f, f): yield [f] + p
Only 3 lines of code. Yields them in lexicographic order. Optionally allows imposition of a maximum part size.
I also have a variation on the above for partitions with a given number of parts:
def sized_partitions(n, k, m = None):
"""Partition n into k parts with a max part of m.
Yield non-increasing lists. m not needed to create generator.
"""
if k == 1:
yield [n]
return
for f in range(n-k+1 if (m is None or m > n-k+1) else m, (n-1)//k, -1):
for p in sized_partitions(n-f, k-1, f): yield [f] + p
After composing the above, I ran across a solution I had created almost 5 years ago, but which I had forgotten about. Besides a maximum part size, this one offers the additional feature that you can impose a maximum length (as opposed to a specific length). FWIW:
def partitions(sum, max_val=100000, max_len=100000):
""" generator of partitions of sum with limits on values and length """
# Yields lists in decreasing lexicographical order.
# To get any length, omit 3rd arg.
# To get all partitions, omit 2nd and 3rd args.
if sum <= max_val: # Can start with a singleton.
yield [sum]
# Must have first*max_len >= sum; i.e. first >= sum/max_len.
for first in range(min(sum-1, max_val), max(0, (sum-1)//max_len), -1):
for p in partitions(sum-first, first, max_len-1):
yield [first]+p
Here's a one-line version of the first one that returns an empty partition when n is 0: def _p(n, m): if not [[(yield (i,)+p) for p in _p(n-i,i)] for i in xrange(min(n,m),0,-1)]: yield () –
Buna
I think the recipe here may qualify as being elegant. It's lean (20 lines long), fast and based upon Kelleher and O'Sullivan's work which is referenced therein:
def aP(n):
"""Generate partitions of n as ordered lists in ascending
lexicographical order.
This highly efficient routine is based on the delightful
work of Kelleher and O'Sullivan.
Examples
========
>>> for i in aP(6): i
...
[1, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 2]
[1, 1, 1, 3]
[1, 1, 2, 2]
[1, 1, 4]
[1, 2, 3]
[1, 5]
[2, 2, 2]
[2, 4]
[3, 3]
[6]
>>> for i in aP(0): i
...
[]
References
==========
.. [1] Generating Integer Partitions, [online],
Available: http://jeromekelleher.net/generating-integer-partitions.html
.. [2] Jerome Kelleher and Barry O'Sullivan, "Generating All
Partitions: A Comparison Of Two Encodings", [online],
Available: http://arxiv.org/pdf/0909.2331v2.pdf
"""
# The list `a`'s leading elements contain the partition in which
# y is the biggest element and x is either the same as y or the
# 2nd largest element; v and w are adjacent element indices
# to which x and y are being assigned, respectively.
a = [1]*n
y = -1
v = n
while v > 0:
v -= 1
x = a[v] + 1
while y >= 2 * x:
a[v] = x
y -= x
v += 1
w = v + 1
while x <= y:
a[v] = x
a[w] = y
yield a[:w + 1]
x += 1
y -= 1
a[v] = x + y
y = a[v] - 1
yield a[:w]
Here is a recursive function, which uses a stack in which we store the numbers of the partitions in increasing order. It is fast enough and very intuitive.
# get the partitions of an integer
Stack = []
def Partitions(remainder, start_number = 1):
if remainder == 0:
print(" + ".join(Stack))
else:
for nb_to_add in range(start_number, remainder+1):
Stack.append(str(nb_to_add))
Partitions(remainder - nb_to_add, nb_to_add)
Stack.pop()
When the stack is full (the sum of the elements of the stack then corresponds to the number we want the partitions), we print it, remove its last value and test the next possible value to be stored in the stack. When all the next values have been tested, we pop the last value of the stack again and we go back to the last calling function. Here is an example of the output (with 8):
Partitions(8)
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1 + 2
1 + 1 + 1 + 1 + 1 + 3
1 + 1 + 1 + 1 + 2 + 2
1 + 1 + 1 + 1 + 4
1 + 1 + 1 + 2 + 3
1 + 1 + 1 + 5
1 + 1 + 2 + 2 + 2
1 + 1 + 2 + 4
1 + 1 + 3 + 3
1 + 1 + 6
1 + 2 + 2 + 3
1 + 2 + 5
1 + 3 + 4
1 + 7
2 + 2 + 2 + 2
2 + 2 + 4
2 + 3 + 3
2 + 6
3 + 5
4 + 4
8
The structure of the recursive function is easy to understand and is illustrated below (for the integer 31):
remainder corresponds to the value of the remaining number we want a partition (31 and 21 in the example above).
start_number corresponds to the first number of the partition, its default value is one (1 and 5 in the example above).
If we wanted to return the result in a list and get the number of partitions, we could do this:
def Partitions2_main(nb):
global counter, PartitionList, Stack
counter, PartitionList, Stack = 0, [], []
Partitions2(nb)
return PartitionList, counter
def Partitions2(remainder, start_number = 1):
global counter, PartitionList, Stack
if remainder == 0:
PartitionList.append(list(Stack))
counter += 1
else:
for nb_to_add in range(start_number, remainder+1):
Stack.append(nb_to_add)
Partitions2(remainder - nb_to_add, nb_to_add)
Stack.pop()
Last, a big advantage of the function Partitions shown above is that it adapts very easily to find all the compositions of a natural number (two compositions can have the same set of numbers, but the order differs in this case):
we just have to drop the variable start_number and set it to 1 in the for loop.
# get the compositions of an integer
Stack = []
def Compositions(remainder):
if remainder == 0:
print(" + ".join(Stack))
else:
for nb_to_add in range(1, remainder+1):
Stack.append(str(nb_to_add))
Compositions(remainder - nb_to_add)
Stack.pop()
Example of output:
Compositions(4)
1 + 1 + 1 + 1
1 + 1 + 2
1 + 2 + 1
1 + 3
2 + 1 + 1
2 + 2
3 + 1
4
# -*- coding: utf-8 -*-
import timeit
ncache = 0
cache = {}
def partition(number):
global cache, ncache
answer = {(number,), }
if number in cache:
ncache += 1
return cache[number]
if number == 1:
cache[number] = answer
return answer
for x in range(1, number):
for y in partition(number - x):
answer.add(tuple(sorted((x, ) + y)))
cache[number] = answer
return answer
print('To 5:')
for r in sorted(partition(5))[::-1]:
print('\t' + ' + '.join(str(i) for i in r))
print(
'Time: {}\nCache used:{}'.format(
timeit.timeit(
"print('To 30: {} possibilities'.format(len(partition(30))))",
setup="from __main__ import partition",
number=1
), ncache
)
)
or https://gist.github.com/sxslex/dd15b13b28c40e695f1e227a200d1646
I don't know if my code is the most elegant, but I've had to solve this many times for research purposes. If you modify the
sub_nums
variable you can restrict what numbers are used in the partition.
def make_partitions(number):
out = []
tmp = []
sub_nums = range(1,number+1)
for num in sub_nums:
if num<=number:
tmp.append([num])
for elm in tmp:
sum_elm = sum(elm)
if sum_elm == number:
out.append(elm)
else:
for num in sub_nums:
if sum_elm + num <= number:
L = [i for i in elm]
L.append(num)
tmp.append(L)
return out
There must be something wrong: I get [1,1], [1, 1], [2], [1, 1] for make_partitions(2). –
Watchdog
F(x,n) = \union_(i>=n) { {i}U g| g in F(x-i,i) }
Just implement this recursion. F(x,n) is the set of all sets that sum to x and their elements are greater than or equal to n.
Interesting; do you generate duplicate samples which the
union combines, and if so, how is the asymptotic perforance for large X? –
Hoffman I do not understand what you are doing. Can you explain it a little bit ? –
Extractive
© 2022 - 2024 — McMap. All rights reserved.