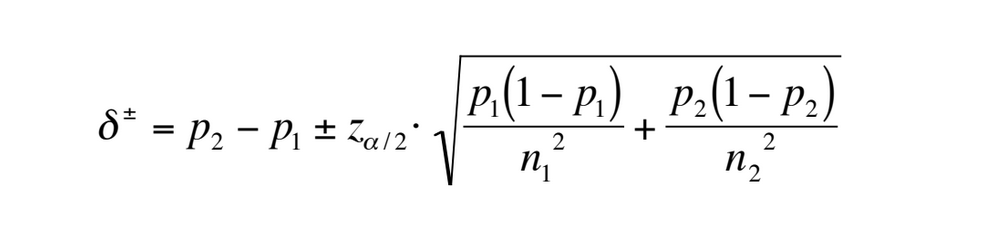Confidence interval for the difference between two proportions in Python

Question

For example, in an AB test the A population could have 1000 data points, of which 100 are successes. While B could have 2000 data points and 220 successes. This gives A a success proportion of 0.1 and B 0.11, the delta of which is 0.01. How can I calculate this confidence interval around this delta in python?

Stats models can do this for one sample, but seemingly does not have a package to deal with the difference between two samples as is necessary for an AB test. (http://www.statsmodels.org/dev/generated/statsmodels.stats.proportion.proportion_confint.html)

Flashboard

docs.scipy.org/doc/scipy-0.14.0/reference/generated/… or #753419 ...? – Polytheism

This is an unusual paradigm. Most often, when two populations are compared the hypothesis would be that their probabilities of success are equal. Following from this confidence intervals would be calculated around p=0. This might be the explanation why you aren't getting any answers here. – Cardiomegaly

Disagree, @BillBell. The confidence interval is build around the point estimate for the difference in the two proportions, which is not a function of the hypothesis, or any of the values related to the hypothesis. The confidence limits are calculated based on how variable that point estimate is. – Respiratory

Answer 1

statsmodels package now has confint_proportions_2indep, which gets the confidence interval for comparing two proportions you can check details in docs https://www.statsmodels.org/stable/generated/statsmodels.stats.proportion.confint_proportions_2indep.html

Angara

Answer 2

I couldn't find a function for this from Statsmodels. However, this website goes over the maths for generating the confidence interval as well as being the source of the below function:

def two_proprotions_confint(success_a, size_a, success_b, size_b, significance = 0.05):
    """
    A/B test for two proportions;
    given a success a trial size of group A and B compute
    its confidence interval;
    resulting confidence interval matches R's prop.test function

    Parameters
    ----------
    success_a, success_b : int
        Number of successes in each group

    size_a, size_b : int
        Size, or number of observations in each group

    significance : float, default 0.05
        Often denoted as alpha. Governs the chance of a false positive.
        A significance level of 0.05 means that there is a 5% chance of
        a false positive. In other words, our confidence level is
        1 - 0.05 = 0.95

    Returns
    -------
    prop_diff : float
        Difference between the two proportion

    confint : 1d ndarray
        Confidence interval of the two proportion test
    """
    prop_a = success_a / size_a
    prop_b = success_b / size_b
    var = prop_a * (1 - prop_a) / size_a + prop_b * (1 - prop_b) / size_b
    se = np.sqrt(var)

    # z critical value
    confidence = 1 - significance
    z = stats.norm(loc = 0, scale = 1).ppf(confidence + significance / 2)

    # standard formula for the confidence interval
    # point-estimtate +- z * standard-error
    prop_diff = prop_b - prop_a
    confint = prop_diff + np.array([-1, 1]) * z * se
    return prop_diff, confint

Flashboard

Answer 3

The sample sizes don't have to be equal. The confidence interval for two proportions is

p1 and p2 are the observed probabilities, computed over their respective samples n1 and n2.

For more please see this white paper.

Blagoveshchensk

I don't think this answers the question. As the authors of that paper say, "Note that we don't make any claims about the magnitude of the difference between p2 and p1 in the entire population — only that it exists." The question is about constructing a confidence interval around a value of 0.11, not zero. – Cardiomegaly

I agree, if that's the question, then what's the null hypothesis? – Blagoveshchensk

I don't think the (ordinary) theory applies. (Not that anyone ever observes such niceties.) You can't take samples, calculate the difference between the sample proportions, and then pretend that you were testing that the difference was 0.11 before you took the samples. It's not sporting. – Cardiomegaly

Would a bootstrap approach solve this problem in some sense? – Worthen

@BillBell You can absolutely start out with the goal of estimating the difference in proportions between two populations, for example, two populations with different treatments. Then, the correct statistical method would be to calculate a confidence interval for the difference in proportions. Not everything has to involve hypothesis tests. If you want, after the confidence interval is calculated, you can note whether it includes certain values of interest, such as some clinically-relevant difference, or zero. – Respiratory