Python: Is there a way to plot a "partial" surface plot with Matplotlib?

Question

I wanted to plot a "partial" surface plot like the following one with Matplotlib

Note that it's not a complete meshgrid on X-Y plane but missing a corner from top view. The following is the code I tried but didn't work.

import numpy as np
from matplotlib import pyplot
from mpl_toolkits.mplot3d import Axes3D

X = np.array([[0,1],
              [0,1,2],
              [0,1,2,3],
             ])
Y = np.array([[0,0],
              [1,1,1],
              [2,2,2,2],
             ])
Z = np.array([[0.5, 0.6],
              [0.7, 0.8, 0.9],
              [1.0, 1.1, 1.2, 1.3],
             ])
fig = pyplot.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X,Y,Z)

The error being:

ValueError: setting an array element with a sequence.

Any pointer would be appreciated! Thanks!

Groundsel

Answer 1

You can do this easily by using np.nan values for Z in the regions you don't want to plot. Here's a modified version of this example but with the cut, as show below:

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.gca(projection='3d')
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(.5*R)

Z[X+Y>4.] = np.nan  # the diagonal slice

surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm,
                       linewidth=0, antialiased=False, vmin=-1, vmax=1)
ax.set_zlim(-1.01, 1.01)

ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))

fig.colorbar(surf, shrink=0.5, aspect=5)

plt.show()

Note here also that I had to use vmin and vmax keywords in the plot command or the color scaling would be thrown by the nans.

Hoenir

Clean solution! I kept trying this, but didn't realize I had to set the limits to deal with the missing values. – Maddock

@Crebit: Thanks. It does seem that matplotlib should be able to ignore the nans in its limit calculations. Maybe there's a way to do it now, or else it might be worth a bug report/feature request. – Hoenir

I found that matplotlib automatically creates partial surface plots now in the presence of nan values in Z, but in order for the color of the surface plot to not be pulled down to the nan temperature, I could simply enforce a feasible range for non-nan values using vmin=0, vmax=1 as you showed here. Thanks! – Stanfordstang

To get the appropriate color range I used vmin=np.nanmin(Z) and vmax=np.nanmax(Z). I'm not sure if this works in general though. – Arteritis

Answer 2

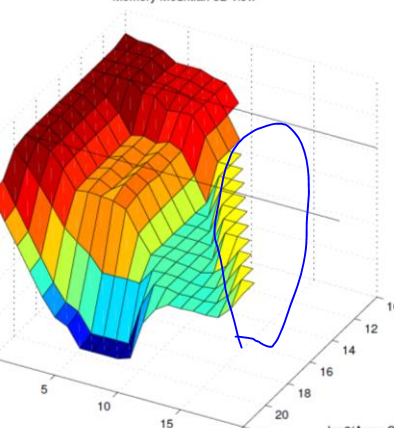
EDIT: Please see tom10's answer. His solution works by setting the values of the excluded part to np.nans.

It looks like matplotlib's plot_surface doesn't accept np.nans as coordinates, so that won't work either. If I understand your question correctly, then I have at least a duct tape solution to offer:

If instead of setting the "cut out" points to zero like MEVIS3000 suggests, you set them to the last value in that dimension, then your 2d arrays will all have same size and the surface will look like it cuts there.

I added some more data points to your example to make it clearer. This is the starting point (where the whole surface is visible):

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


X = np.array([[0, 1, 2, 3, 4, 5],
              [0, 1, 2, 3, 4, 5],
              [0, 1, 2, 3, 4, 5],
             ])
Y = np.array([[0, 0, 0, 0, 0, 0],
              [1, 1, 1, 1, 1, 1],
              [2, 2, 2, 2, 2, 2],
             ])
Z = np.array([[0.5, 0.4, 0.35, 0.32, 0.312, 0.3],
              [0.9, 0.7, 0.60, 0.55, 0.525, 0.5],
              [1.0, 1.1, 1.20, 1.30, 1.400, 1.5],
             ])


fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X,Y,Z)

plt.show()

The resulting surface looks like this (from the upside):

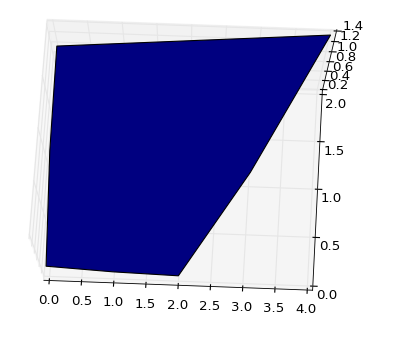
Now, if we adjust the arrays so that we replace the "missing" values with previous values in that row we can leave out a part of the surface:

X = np.array([[0, 1, 2, 2, 2, 2],  # Notice the sequence 0, 1, 2, 2, 2...
              [0, 1, 2, 3, 3, 3],  # Here starting from 3
              [0, 1, 2, 3, 4, 4],  # Here starting from 4
             ])
Y = np.array([[0, 0, 0, 0, 0, 0],  # Here we don't need to do anything
              [1, 1, 1, 1, 1, 1],
              [2, 2, 2, 2, 2, 2],
             ])
Z = np.array([[0.5, 0.4, 0.35, 0.35, 0.35, 0.35],  # Here like in X: repeats from 0.35
              [0.9, 0.7, 0.60, 0.55, 0.55, 0.55],
              [1.0, 1.1, 1.20, 1.30, 1.40, 1.40],
             ])

The resulting chart looks like this (again from the same view):

This is not a pretty fix, but it is one way to do it. I will leave you with the problem of automating the "cutoff" somehow.

Maddock

Answer 3

The sub-arrays must have the same lengths. e.g.:

X = np.array([[0,1,0,0],
              [0,1,2,0],
              [0,1,2,3]
             ])

and so on.

Michelinemichell

Right, currently my solution is to fill those spots with 0s for it to at least work. But the 0s will still appear on the graph. After all 0s are not the same as "nothing". – Groundsel

Ah I see. But I don't think it's generally possible to plot something uncontinuously. And as far as I know, a triangular matrix does consist of zeros, for the "not triangular" part. – Michelinemichell

oh thanks for clarification! I was just trying to describe what it looks like. I'll edit it so that it won't be confusing. – Groundsel