Speed of CPLEX vs CPLEX using SCIP

Question

I am new to LP and have only briefly used PuLP in Python.

1. Why is there a speed difference between SCIP 3.2.1 - CPLEX 12.63 and CPLEX 12.6.3? Doesn't SCIP still use CPLEX for solving?

2. Why will someone use SCIP with CPLEX solver, instead of using CPLEX directly?

Irritating

Some remark: cbc (one of the best open-source MIP-solvers) will be typically the default-solver for pulp. At least within the windows-distribution. – Rivet

Answer 1

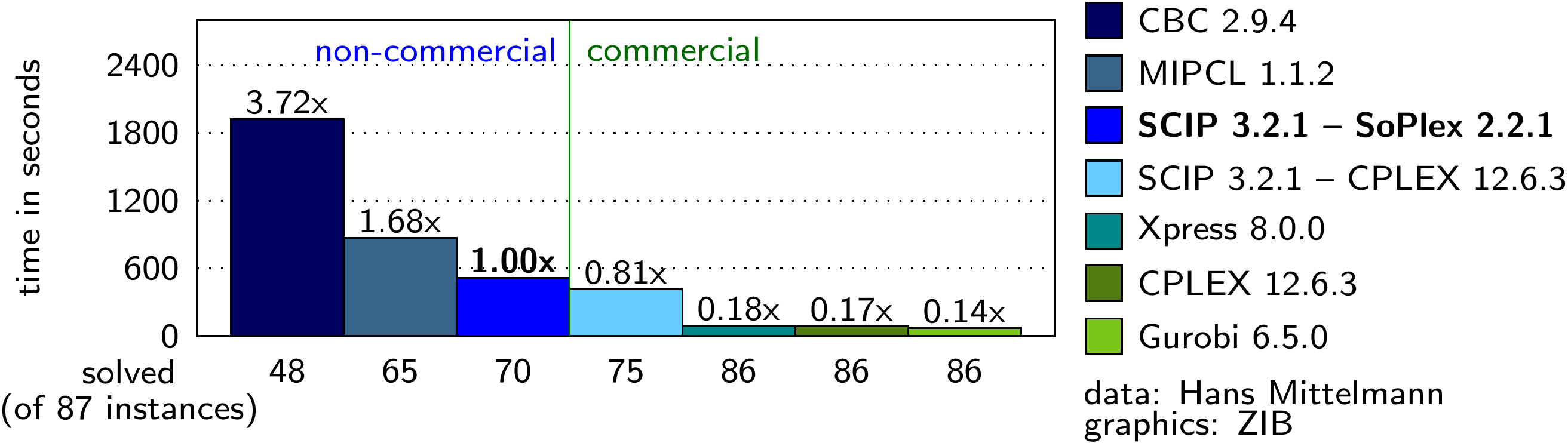
What is this difference about

This plot is not showing a LP-benchmark, but a Mixed-integer programming benchmark.

Mixed-integer programming solvers typically use a branch-and-cut-based algorithm (including heuristics and co.), where a lot of relaxations are solved (in sequence; treating binary-/integer-variables as continuous resulting in an LP-problem).

One decision then is to choose how to solve these relaxed subproblems. The most simple decision (there are many more; e.g. tuning the Simplex-algorithm's parameters; it get's even more complex when solving problems with nonlinear-conic objectives) is to choose the LP-solver.

SoPlex is a LP-solver implementation by the SCIP-team. Meaning:

• SCIP - SoPlex will use SCIP's algorithm for MIP (handling branching, cut-generation and co.) using SoPlex as solver for the internal LP-subproblems
• SCIP - CPLEX will use SCIP's algorithm for MIP using CPLEX as solver for the internal LP-subproblems

Why using SCIP with CPLEX (instead of using a pure CPLEX approach)

The why is not that easy to explain.

• Keep in mind, that all MIP-solvers are heuristics-based and on some problems SCIP will be faster than CPLEX (despite the underlying LP-solver selected).

  Keywords for some theory: NP-hardness (of MIP) and the No free lunch theorem

  • Faster could mean: faster due to the MIP-based strategies, not the speed of the underlying LP-solver so that you may even gain an overall speedup using CPLEX on the subproblems!

• The two solvers (MIP-solvers) are probably also much different in regards to parameters & accessibility (of internal algorithmic components). It's obvious, that you can tune SCIP in a much more general way than CPLEX (because it's open source)

• As mattmilten mentioned in the comments: SCIP and CPLEX are also different in regards to the support of problem-classes which can be solved. One example of this might be the possibility for some special nonlinear-constraints (resulting in a MINLP). Using SCIP for these kind of problems, can still use CPLEX' LP-solver internally (same arguments as above)

Rivet

Worth noting is that SCIP can solve a wide variety of problem classes - more than CPLEX - and sometimes it may be of advantage to still use CPLEX as LP solver while solving a nonconvex MINLP for instance. – Odorous

@Odorous I just added one remark, that sometimes the MIP-based algorithm is faster and an additional speedup could be obtained by using CPLEX' LP-solver for the subproblems. I agree with everything you said. – Rivet