Why doesn't Dijkstra's algorithm work for negative weight edges?

Question

Can somebody tell me why Dijkstra's algorithm for single source shortest path assumes that the edges must be non-negative.

I am talking about only edges not the negative weight cycles.

Playoff

A correct answer with a good example would be: #6799672 – Gadson

Does this answer your question? Negative weights using Dijkstra's Algorithm – Cachexia

Answer 1

Recall that in Dijkstra's algorithm, once a vertex is marked as "closed" (and out of the open set) - the algorithm found the shortest path to it, and will never have to develop this node again - it assumes the path developed to this path is the shortest.

But with negative weights - it might not be true. For example:

       A
      / \
     /   \
    /     \
   5       2
  /         \
  B--(-10)-->C

V={A,B,C} ; E = {(A,C,2), (A,B,5), (B,C,-10)}

Dijkstra from A will first develop C, and will later fail to find A->B->C

---

EDIT a bit deeper explanation:

Note that this is important, because in each relaxation step, the algorithm assumes the "cost" to the "closed" nodes is indeed minimal, and thus the node that will next be selected is also minimal.

The idea of it is: If we have a vertex in open such that its cost is minimal - by adding any positive number to any vertex - the minimality will never change.
Without the constraint on positive numbers - the above assumption is not true.

Since we do "know" each vertex which was "closed" is minimal - we can safely do the relaxation step - without "looking back". If we do need to "look back" - Bellman-Ford offers a recursive-like (DP) solution of doing so.

Displayed

Sorry but I'm not getting any error. First A->B will 5 and A->C will 2. Then B->C will -5. So the value of C will be -5 same as bellman-ford. How is this not giving the right answer? – Woodbury

@tintinmj first, Dijkstra will "close" node A with value of 0. Then, it will look on the minimal valued node, B is 5 and C is 2. The minimal is C, so it will close C with value 2 and will never look back, when later B is closed, it cannot modify the value of C, since it is already "closed". – Displayed

@Displayed How Dijkstra's algorithm won't find the path A -> B -> C? It will first update C's distance to 2, and then B's distance to 5. Assuming that in your graph there are no outgoing edges from C, then we do nothing when visiting C (and its distance is still 2). Then we visit D's adjacent nodes, and the only adjacent node is C, whose new distance is -5. Note that in the Dijkstra's algorithm, we also keep track of the parent from which we reach (and update) the node, and doing it from C, you will get the parent B, and then A, resulting in a correct result. What am I missing? – Overword

@Displayed The problem with your reasoning (I think), and I have seen other people doing it (strangely), is that you think the algorithm will not reconsider nodes whose shortest distance has already been determined (and that we are done with), but this is not correct, and that's why we have the "relaxation" step...We iterate through all nodes of the graph, and, for each of them, we iterate through the adjacent nodes, even if any of the adjacent node might have already been removed from our min-priority queue, for example. – Overword

@Displayed Check this answer to a similar question, where the example actually makes sense: https://mcmap.net/q/129685/-negative-weights-using-dijkstra-39-s-algorithm – Overword

@Axl (1) There is no 'D'. (2) The algorithm does not reconsider nodes whose shortest distance was determined. See the original paper for reference. Dijsktra specicially splits the nodes to the nodes for wbLich the path o{ nrinimum lengti from P is known (set A) and others (sets B,C) . He later specifically satates: Consider all branches z connecting the node just transfeired to set A with nodes R in sets B or C, so he considers relaxing only nodes NOT in A - those who's path is not discovered yet. – Displayed

@Displayed D is a typo, and I meant B. – Overword

@Axl So, tl;dr: Dijkstra's algorithm does NOT recalculate value for any vertex who's distance was already determined. You can think of an algorithm that will - but that's not Dijkstra's Algorithm anymore. – Displayed

@Displayed There are many variants of Dijkstra's algorithm, and the original one only finds the shortest path between 2 nodes, and not between a node and all other ones, which is the algorithm I am talking about, and which is more helpful. – Overword

@Axl This is Dijkstra's Algorithm, by definition. Only difference between this and "one to all shortest path" is - you do not abort when destination is found. Also, please provide a reference for a variant that does re-open already closed nodes. – Displayed

@Displayed For a reference of the algorithm I am talking about, check "Introduction to Algorithms", 3rd edition, by Cormen and friends. – Overword

I think that in that algorithm (it should be on chapter 24), when iterating through the adjacent nodes, it does not care if the adjacent node is still in the min priority queue or not, which is, in my opinion, what the algorithm should do to be useful. – Overword

Prim's algorithm for computing the minimum spanning tree is really similar to that Dijkstra's algorithm, except that it checks if the adjacent node is still on the set, which is logical, since you don't want to create a cycle. – Overword

@Axl I see what your point when referring to this specific variant, but as said- this does not apply to "Dijkstra's Algorithm" as suggested by Dijkstra. You can claim this algorithm is useless, but 15,423 references think otherwise. Both solutions will fail (in different cases though) for negative edges, so I don't really see why one is superior to the other, except for enecdotal cases. – Displayed

@Displayed I don't know well about the original algorithm except for the fact that it computed just the shortest path between 2 nodes, and that's it, but IMO, this algorithm in the book I mentioned before is more useful, even if the running time complexity might be a little bit worse... – Overword

Answer 2

Consider the graph shown below with the source as Vertex A. First try running Dijkstra’s algorithm yourself on it.

When I refer to Dijkstra’s algorithm in my explanation I will be talking about the Dijkstra's Algorithm as implemented below,

So starting out the values (the distance from the source to the vertex) initially assigned to each vertex are,

We first extract the vertex in Q = [A,B,C] which has smallest value, i.e. A, after which Q = [B, C]. Note A has a directed edge to B and C, also both of them are in Q, therefore we update both of those values,

Now we extract C as (2<5), now Q = [B]. Note that C is connected to nothing, so line16 loop doesn't run.

Finally we extract B, after which . Note B has a directed edge to C but C isn't present in Q therefore we again don't enter the for loop in line16,

So we end up with the distances as

Note how this is wrong as the shortest distance from A to C is 5 + -10 = -5, when you go .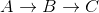

So for this graph Dijkstra's Algorithm wrongly computes the distance from A to C.

This happens because Dijkstra's Algorithm does not try to find a shorter path to vertices which are already extracted from Q.

What the line16 loop is doing is taking the vertex u and saying "hey looks like we can go to v from source via u, is that (alt or alternative) distance any better than the current dist[v] we got? If so lets update dist[v]"

Note that in line16 they check all neighbors v (i.e. a directed edge exists from u to v), of u which are still in Q. In line14 they remove visited notes from Q. So if x is a visited neighbour of u, the path is not even considered as a possible shorter way from source to v.

In our example above, C was a visited neighbour of B, thus the path was not considered, leaving the current shortest path unchanged.

This is actually useful if the edge weights are all positive numbers, because then we wouldn't waste our time considering paths that can't be shorter.

So I say that when running this algorithm if x is extracted from Q before y, then its not possible to find a path - which is shorter. Let me explain this with an example,

As y has just been extracted and x had been extracted before itself, then dist[y] > dist[x] because otherwise y would have been extracted before x. (line 13 min distance first)

And as we already assumed that the edge weights are positive, i.e. length(x,y)>0. So the alternative distance (alt) via y is always sure to be greater, i.e. dist[y] + length(x,y)> dist[x]. So the value of dist[x] would not have been updated even if y was considered as a path to x, thus we conclude that it makes sense to only consider neighbors of y which are still in Q (note comment in line16)

But this thing hinges on our assumption of positive edge length, if length(u,v)<0 then depending on how negative that edge is we might replace the dist[x] after the comparison in line18.

So any dist[x] calculation we make will be incorrect if x is removed before all vertices v - such that x is a neighbour of v with negative edge connecting them - is removed.

Because each of those v vertices is the second last vertex on a potential "better" path from source to x, which is discarded by Dijkstra’s algorithm.

So in the example I gave above, the mistake was because C was removed before B was removed. While that C was a neighbour of B with a negative edge!

Just to clarify, B and C are A's neighbours. B has a single neighbour C and C has no neighbours. length(a,b) is the edge length between the vertices a and b.

Branson

Like you said, the better way to solve this is to use heapq.heappush method after each comparison. We push back the updated distance into the queue. Under this condition, the Dijkstra's can work on negative weights. I tried, and the result came out as 0,5,-5 – Gaitskell

"the path source to x to u is not even considered"; did you mean source to u to x? – Improvised

@slmatrix thanks for catching that, yes, I meant that the path from source to u to x, because x is a neighbor of u. – Branson

Actually, in the 16th line of the code there's no constraint that v should be in Q (the only 'constraint' is in the comment), so your example fails. Specifically, in your explanation the line "Note B has a directed edge to C but C isn't present in Q therefore we again don't enter the for loop in line16" is wrong, and we actually enter the loop once again and update the last edge, so that B = 1. So, the Dijkstra's algorithm runs correctly on your example. – Mozell

Answer 3

Dijkstra's algorithm assumes paths can only become 'heavier', so that if you have a path from A to B with a weight of 3, and a path from A to C with a weight of 3, there's no way you can add an edge and get from A to B through C with a weight of less than 3.

This assumption makes the algorithm faster than algorithms that have to take negative weights into account.

Aten

Answer 4

Correctness of Dijkstra's algorithm:

We have 2 sets of vertices at any step of the algorithm. Set A consists of the vertices to which we have computed the shortest paths. Set B consists of the remaining vertices.

Inductive Hypothesis: At each step we will assume that all previous iterations are correct.

Inductive Step: When we add a vertex V to the set A and set the distance to be dist[V], we must prove that this distance is optimal. If this is not optimal then there must be some other path to the vertex V that is of shorter length.

Suppose this some other path goes through some vertex X.

Now, since dist[V] <= dist[X] , therefore any other path to V will be atleast dist[V] length, unless the graph has negative edge lengths.

Thus for dijkstra's algorithm to work, the edge weights must be non negative.

Acquiescence

Answer 5

Try Dijkstra's algorithm on the following graph, assuming A is the source node and D is the destination, to see what is happening:

Note that you have to follow strictly the algorithm definition and you should not follow your intuition (which tells you the upper path is shorter).

The main insight here is that the algorithm only looks at all directly connected edges and it takes the smallest of these edge. The algorithm does not look ahead. You can modify this behavior , but then it is not the Dijkstra algorithm anymore.

Womanize

Sorry but I'm not getting any error. First A->B will 1 and A->C will 100. Then B->D will 2. Then C->D will -4900. So the value of D will be -4900 same as bellman-ford. How is this not giving the right answer? – Woodbury

@tintinmj If you have an outgoing edge from D, it will get visited before D's distance is decreased and hence not updated after it is. This will then result in an error for sure. If you consider D's 2 as the final distance already after scanning outgoing edges, even this graph results in an error. – Lachance

@Womanize Sorry for asking after such a long time but, am I on the right track here? First A->B will be 1 and A->C will be 100. Then B is explored and sets B->D to 2. Then D is explored because currently it has the shortest path back to the source? Would I be correct in saying that if B->D was 100, C would've been explored first? I understand all other examples people give except yours. – Pampa

@PejmanPoh from my understanding, if B->D was 100, since A->C is higher in the HeapStructure which will be used, the extract min will return A->C first which means the next found shortest path will be the path to C, after that the path from C->D which is with weight -5000 will be the obvious choice, leading us to a conclusion that the shortest path would be from A->C->D and i am pretty sure this would be the normal behaviour. So sometimes when we have negative cycles we still might get the right value for the shortest path, but definitely not always, this is an example where we will not.. – Cyclopentane

Well, if you have a cycle that has in sum a negative weight, then there is strictly speaking no shortest path. Because for each path P that claims to be the shortest path, you can find a path P' that is shorter by including one additional iteration of the cycle. – Womanize

Yes, you can phrase it like that and show it by some trivial examples. However, I would rather say the Dijkstra algorithm cannot be applied for graphs with negative edge weights because the requirements are not met and if you apply it you do not know whether the result is optimal or not. – Womanize

Answer 6

Dijkstra's Algorithm assumes that all edges are positive weighted and this assumption helps the algorithm run faster ( O(E*log(V) ) than others which take into account the possibility of negative edges (e.g bellman ford's algorithm with complexity of O(V^3)).

This algorithm wont give the correct result in the following case (with a -ve edge) where A is the source vertex:

Here, the shortest distance to vertex D from source A should have been 6. But according to Dijkstra's method the shortest distance will be 7 which is incorrect.

Also, Dijkstra's Algorithm may sometimes give correct solution even if there are negative edges. Following is an example of such a case:

However, It will never detect a negative cycle and always produce a result which will always be incorrect if a negative weight cycle is reachable from the source, as in such a case there exists no shortest path in the graph from the source vertex.

Elamitic

Answer 7

You can use dijkstra's algorithm with negative edges not including negative cycle, but you must allow a vertex can be visited multiple times and that version will lose it's fast time complexity.

In that case practically I've seen it's better to use SPFA algorithm which have normal queue and can handle negative edges.

Donell

does anyone know what will be the time complexity of Dijkstra if we remove the checks for visited nodes? – Granados

@Granados Then it is no longer Dijkstra. That is just a standard Ford algorithm. The very definition of Dijkstra is when you do a Ford algorithm, but in such order that you can visit each vertex only once. – Tbilisi

Answer 8

Recall that in Dijkstra's algorithm, once a vertex is marked as "closed" (and out of the open set) -it assumes that any node originating from it will lead to greater distance so, the algorithm found the shortest path to it, and will never have to develop this node again, but this doesn't hold true in case of negative weights.

Annabal

Answer 9

Adding few points to the explanation, on top of the previous answers, for the following simple example,

1. Dijktra's algorithm being greedy, it first finds the minimum distance vertex C from the source vertex A greedily and assigns the distance d[C] (from vertex A) to the weight of the edge AC.
2. The underlying assumption is that since C was picked first, there is no other vertex V in the graph s.t. w(AV) < w(AC), otherwise V would have been picked instead of C, by the algorithm.
3. Since by above logic, w(AC) <= w(AV), for all vertex V different from the vertices A and C. Now, clearly any other path P that starts from A and ends in C, going through V , i.e., the path P = A -> V -> ... -> C, will be longer in length (>= 2) and total cost of the path P will be sum of the edges on it, i.e., cost(P) >= w(AV) >= w(AC), assuming all edges on P have non-negative weights, so that C can be safely removed from the queue Q, since d[C] can never get smaller / relaxed further under this assumption.
4. Obviously, the above assumption does not hold when some.edge on P is negative, in a which case d[C] may decrease further, but the algorithm can't take care of this scenario, since by that time it has removed C from the queue Q.

Hardily

Answer 10

The other answers so far demonstrate pretty well why Dijkstra's algorithm cannot handle negative weights on paths.

But the question itself is maybe based on a wrong understanding of the weight of paths. If negative weights on paths would be allowed in pathfinding algorithms in general, then you would get permanent loops that would not stop.

Consider this:

A  <- 5 ->  B  <- (-1) ->  C <- 5 -> D

What is the optimal path between A and D?

Any pathfinding algorithm would have to continuously loop between B and C because doing so would reduce the weight of the total path. So allowing negative weights for a connection would render any pathfindig algorithm moot, maybe except if you limit each connection to be used only once.

So, to explain this in more detail, consider the following paths and weights:

Path               | Total weight
ABCD               | 9
ABCBCD             | 7
ABCBCBCD           | 5
ABCBCBCBCD         | 3
ABCBCBCBCBCD       | 1
ABCBCBCBCBCBCD     | -1
...

So, what's the perfect path? Any time the algorithm adds a BC step, it reduces the total weight by 2.

So the optimal path is A (BC) D with the BC part being looped forever.

Since Dijkstra's goal is to find the optimal path (not just any path), it, by definition, cannot work with negative weights, since it cannot find the optimal path.

Dijkstra will actually not loop, since it keeps a list of nodes that it has visited. But it will not find a perfect path, but instead just any path.

Paisano

Nope, because the optimal path would continuously jump between B and C. Imagine this: The algorithm already found this path: A B C. The current weight is 4 (5-1). Now at C it could go to D, which would give a total weight of 9. But if it instead goes back to B, it would find the path ABCBCD, which has a weight of 7, which is better. But then again, it could take ABCBCBCD, which has a weight of 5. So intrinsically, there is an endless loop if you want to find the optimal path. The optimal path with negative weights would be A (BC) D with the BC part repeated endlessly. – Paisano

With negative weights, Dijkstra might find A path, but not the optimal path (since an optimal path is not physically possible with negative weights). Thus Dijkstra (as any other pathfinding algo) cannot "work", as in return a perfect path. – Paisano

There can be optimal path if there is a restriction saying that all vertexes can be visited at most 1 time. This assumption is implicit in the OP's question. If you permit visiting the same node twice, then there is essentially a negative cycle. – Cislunar

@TYeung That is true, but then it's not Dijkstra. And the question was about Dijkstra, not about other algos. – Paisano

Answer 11

I'll add my 2 cents here: with a SMALL ADAPTATION Dijkstra's CAN WORK with negative weight edges. Consider this graph:

This is Dijkstra's algorithm adapted in python 3.9:

import heapq

# A graph has nodes, nodes have edges, edges are nodes with weights
graph1 = {
    'A': {'B': 1, 'C': 10},
    'B': {'D': 2},
    'C': {'D': -8},
    'D': {}
}

def dijkstra_with_negative(graph: dict[str, dict[str, int]], source: str, dest: str):
    queue = []
    visited = []
    dist = {node: float('inf') for node in graph}
    previous = {}

    # Improvement for negative graph: a heap doesn't need to be used.
    # Try instead collections.deque, optimized for append and pop
    heapq.heappush(queue, (0, source))
    dist[source] = 0

    while len(queue) > 0:
        (nodeDist, node) = heapq.heappop(queue)
        
        if nodeDist > dist[dest]:
            print('For non negative, would exit now with:')
            print(get_path(dist, previous, dest))
            # break

        if node in visited:
            #avoid revisits and negative cycles that would result in infinite loop
            continue

        visited.append(node)

        for edge, edgeDist in graph[node].items():
            newDist = edgeDist + dist[node]
            if newDist < dist[edge]:
                dist[edge] = newDist
                previous[edge] = node
                heapq.heappush(queue, (newDist, edge))

    # Check for negative weight cycles
    for node in graph:
        for edge, edgeDist in graph[node].items():
            assert dist[node] + edgeDist >= dist[edge], "Negative weight cycle detected!"
    
    # print path with nodes and distances
    print('Final path:')
    print(get_path(dist, previous, dest))

def get_path(dist: list, previous: list, node: str) -> list:
    path = []
    while node is not None:
        path.append((node, dist[node]))
        node = previous.get(node, None)
    
    path.reverse()
    return path

dijkstra_with_negative(graph1, 'A', 'D')

As you can see, the adaptation is very small:

1. You don't break the loop because at any point a negative path can make the path smaller
2. You check for negative cycle to give error if present
3. Optional: you could use a normal list instead of a heap, to avoid extra processing since all nodes will be visited

Folsom

Answer 12

I was just learning this, adding my two cents here because I think the biggest confusion is the difference between implementation detail and the theory. The original algorithm is proof based...so the idea is that you don't look back on something you already deemed shortest. Once it's shortest so far, it's just gone, it doesn't exist anymore to you aside from the fact that the shortest distance is now some number d.

So according to the original THEORY, implementation wise, it would use a heap to keep BOTH the vertex and distance. For example, you have array [(0,S),(inf,A),(inf,B)] as your starting point.

So is a case where you have

remember that you delete the minimum in each iteration, so literally you only have [(3,A),(4,B)] in the first loop, because you popped S. Next you pop A, so the only thing left in your heap is [(4,B)]

Yes you would think, oh, after I expand B, there is an edge to A, I'll just update it. But then you look at the heap, where you keep your distance...it's empty. So it's not because you can't expand B, it's because A can't be updated (you don't look back).

So if you were to use some other structure to keep track of things, then yes, it could handles some negative cases like the one above, but then that wouldn't be the original algorithm's idea because you looked back.

Insulin

Answer 13

In Unweighted graph

Dijkstra can even work without set or priority queue, even if you just use STACK the algorithm will work but with Stack its time of execution will increase

Dijkstra don't repeat a node once its processed becoz it always tooks the minimum route , which means if you come to that node via any other path it will certainly have greater distance

For ex - (0) /
6 5 /
(2) (1) \ / 4 7 \ / (9)

here once you get to node 1 via 0 (as its minimum out of 5 and 6)so now there is no way you can get a minimum value for reaching 1 because all other path will add value to 5 and not decrease it

more over with Negative weights it will fall into infinite loop

Globetrotter

"Dijkstra can even work without set or priority queue, even if you just use STACK" I do not believe that is the case, you need a priority queue to retain the invariant "next popped node has the shortest distance from the start". – Archaism

Answer 14

In Unweighted graph Dijkstra Algo will fall into loop if it has negative weight

In Directed graph Dijkstra Algo will give RIGHT ANSWER except in case of Negative Cycle

Who says Dijkstra never visit a node more than once are 500% wrong also who says Dijkstra can't work with negative weight are wrong

Globetrotter

i.stack.imgur.com/fODnw.png If your algorithm give the shortest path from A to E, then your algorithm is not Dijkstra. No negative cycle here (no cycle at all, actually). Dijkstra's answer is that shortest path A→E is A→B→E, length 2. When A→C→D→B→E is shorter. But when path ACDB have found a path length -1 to B, it is too late: B has already been closed, so no outgoing arc from B will be revisited (or else, it is Ford, no Dijkstra). – Tbilisi