How to use the ccf() method in the statsmodels library?

Question

I am having some trouble with the ccf() method in the (Python) statsmodels library. The equivalent operation works fine in R.

ccf produces a cross-correlation function between two variables, A and B in my example. I am interested to understand the extent to which A is a leading indicator for B.

I am using the following:

import pandas as pd
import numpy as np
import statsmodels.tsa.stattools as smt

I can simulate A and B as follows:

np.random.seed(123)
test = pd.DataFrame(np.random.randint(0,25,size=(79, 2)), columns=list('AB'))

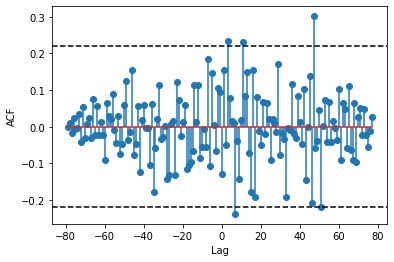
When I run ccf, I get the following:

ccf_output = smt.ccf(test['A'],test['B'], unbiased=False)
ccf_output    
array([ 0.09447372, -0.12810284,  0.15581492, -0.05123683,  0.23403344,
    0.0771812 ,  0.01434263,  0.00986775, -0.23812752, -0.03996113,
   -0.14383829,  0.0178347 ,  0.23224969,  0.0829421 ,  0.14981321,
   -0.07094772, -0.17713121,  0.15377192, -0.19161986,  0.08006699,
   -0.01044449, -0.04913098,  0.06682942, -0.02087582,  0.06453489,
    0.01995989, -0.08961562,  0.02076603,  0.01085041, -0.01357792,
    0.17009109, -0.07586774, -0.0183845 , -0.0327533 , -0.19266634,
   -0.00433252, -0.00915397,  0.11568826, -0.02069836, -0.03110162,
    0.08500599,  0.01171839, -0.04837527,  0.10352341, -0.14512205,
   -0.00203772,  0.13876788, -0.20846099,  0.30174408, -0.05674962,
   -0.03824093,  0.04494932, -0.21788683,  0.00113469,  0.07381456,
   -0.04039815,  0.06661601, -0.04302084,  0.01624429, -0.00399155,
   -0.0359768 ,  0.10264208, -0.09216649,  0.06391548,  0.04904064,
   -0.05930197,  0.11127125, -0.06346119, -0.08973581,  0.06459495,
   -0.09600202,  0.02720553,  0.05152299, -0.0220437 ,  0.04818264,
   -0.02235086, -0.05485135, -0.01077366,  0.02566737])

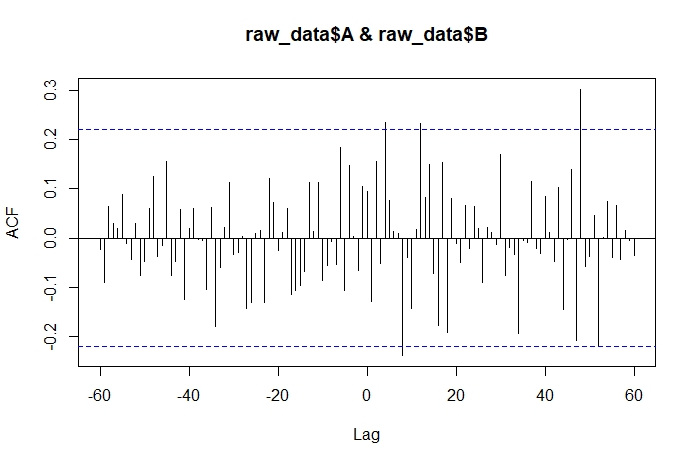
Here is the outcome I am trying to get to (produced in R):

The problem is this: ccf_output is giving me only the correlation values for lag 0 and to the right of Lag 0. Ideally, I would like the full set of lag values (lag -60 to lag 60) so that I can produce something like the above plot.

Is there a way to do this?

Copperplate

Answer 1

The statsmodels ccf function only produces forward lags, i.e. Corr(x_[t+k], y_[t]) for k >= 0. But one way to compute the backwards lags is by reversing the order of the both the input series and the output.

backwards = smt.ccf(test['A'][::-1], test['B'][::-1], adjusted=False)[::-1]
forwards = smt.ccf(test['A'], test['B'], adjusted=False)
ccf_output = np.r_[backwards[:-1], forwards]

Note that both backwards and forwards contained lag 0, so we had to remove that from one of them when combining them.

Edit another alternative is to reverse the order of the arguments and the output:

backwards = sm.tsa.ccf(test['B'], test['A'], adjusted=False)[::-1]

Standoff

That works perfectly. Small note - I believe "adjusted" should be "unbiased".: – Copperplate

in other words . . . backwards = sm.tsa.ccf(test['B'], test['A'], unbiased = False)[::-1] – Copperplate

Good point. However, note that the unbiased argument will be deprecated in the upcoming v0.12 release of statsmodels in favor of the adjusted argument. – Standoff

Answer 2

The desired cross-correlation plot can be obtained as below (from which we can estimate the best lag for CCF by finding the peak):

import matplotlib.pylab as plt
#np.random.seed(123)
#test = pd.DataFrame(np.random.randint(0,25,size=(79, 2)), columns=list('AB'))
#backwards = smt.ccf(test['B'], test['A'], unbiased=False)[::-1]
#forwards = smt.ccf(test['A'], test['B'], unbiased=False)
#ccf_output = np.r_[backwards[:-1], forwards]
plt.stem(range(-len(ccf_output)//2, len(ccf_output)//2), ccf_output)
plt.xlabel('Lag')
plt.ylabel('ACF')
# 95% UCL / LCL
plt.axhline(-1.96/np.sqrt(len(test)), color='k', ls='--') 
plt.axhline(1.96/np.sqrt(len(test)), color='k', ls='--')

Burdock

The best solution available all over the internet on this question! – Primus