Raycasting engine rendering creating slight distortion increasing towards edges of screen

Question

I'm developing a basic raycasting engine for HTML5 canvas, of the variety used in games like Wolfenstein 3D and Doom, as a learning exercise / hobby project. I've got to the point where I have walls rendering on the canvas with texture mapping, which is working pretty well after a fair bit of effort getting the intersection testing functions right.

I am correcting for the "fishbowl" / "fisheye" distortion effect (caused by increasing distances to intersection points as the angle from the centre of the screen increases), but I still have a very slight, but noticeable, curved distortion at the edges of the screen. This can be seen in the following image (I have drawn straight red lines to make the effect more obvious):

Can anyone shed light on what the source of this distortion is? It's not a huge issue but I haven't been able to figure out the cause, so I'm clearly missing something and I'm sure someone must know the answer. I've searched the problem pretty extensively and there isn't much information online, but I did find the following snippet in a forum post:

"The warping caused by using constant angular increments instead of horizon projection is another matter entirely - thats a lateral stretching/bunching effect and although usualy its only a barely noticable effect (for reasonable FOV, although the fact that you can define a 999999 degree FOV should ring bells), there simply isnt any reasonable way at all to compensate besides doing it right to begin with.. the angles are wrong using fixed increments and thats all there is to that."

This sounds like it might be referring to the same distortion I am experiencing, but it doesn't provide much help or insight other than suggesting fixed angle increments are the source of the problem (it's a curved distortion which increases towards the edges of the screen, which seems to fit with what this suggests). The function I am using to correct the distortions is:

function m_CorrectRayLengthDistortion( dist, angleFromCentre ){

    return dist * Math.cos( MOD_Maths.degToRad( angleFromCentre ) );
}

MOD_Maths being a utility module (used in this case to convert the angle from degrees to radians so the cosine function can use it).

Any help on this is greatly appreciated, and if anyone answers this it will hopefully provide a guide to anyone experiencing the issue in future, given the aparrent lack of information on the subject that is available online.

Thanks :)

Porty

That does not resemble ray-casting from Wolfenstein / Doom at all. They used columns multiple pixels wide for walls, but here you seem to have columns 1 pixel wide; that, or your texture mapping is way off. – Reflect

Yes, I am using 1 pixel wide columns, but this is a trivial difference from the games I mentioned (I'm just attempting to get a higher resolution out of the same rendering system). I'm not trying to replicate the retro look of Doom or Wolf3D, that isn't the point. – Porty

Answer 1

I solved this problem properly quite a while ago, but haven't got round to updating the answer until now. I have removed my previous answer which was incorrect (it gave almost correct results but by an indirect method, thanks to my lack of understanding of the root cause of the problem).

As Sam mentioned in his earlier comment, the root cause of the issue is that fixed angle increments are actually not correct if you want to achieve equally-spaced columns (which are necessary for the rendered result to look undistorted). This was mentioned in a forum post here, but although I found this I didn't fully understand why this was the case, or how to remedy the problem, until much later.

To achieve equally spaced columns on the screen, it stands to reason that each ray must travel from the point of view and pass through a pixel which is equally spaced along the projection surface, which means that as the rays move further from the central pixel of the screen, the increment by which the angle from the look direction increases gets gradually smaller. This is illustrated by the following picture (apologies, it isn't exactly a work of art):

With small fields of view the problem is not very noticeable, but becomes more problematic as the field of view increases (in my diagram the field of view is quite large to clearly illustrate the problem). To correctly calculate the ray angle increments, the following process must be used:

Where:

ang = ray angle from the look direction, whose ray passes through the central x coordinate of the screen;
opp = opposite side (equivalent to the distance of the screen X coordinate through which the ray passes from the screen X coordinate of the central pixel);
adj = adjacent side (equivalent to the distance from the point of view to the projection surface, which will be predetermined in code somewhere);

We can use the following formula (derivation included for clarity):

tan( ang ) = opp / adj
ang = atan( opp / adj )
ang = atan( ( pixel x coord - half screen width ) / dist to projection surface )

Javascript code example from my engine:

for( var x = 0; x < canvasSizeX; x++ ){

    var xAng = _atan( ( x - canvasSizeHalfX ) / m_DistToProjSurf );
    xRayAngles.push( xAng );
}

Due to the somewhat scarce nature of information on raycasting engines which is available online, and also due to the fact this particular issue isn't explicitly covered in any of the main tutorials which are out there, I wanted to update this post with the correct information in case anyone else has the same problem I did and doesn't understand why. Hopefully this will help someone.

Porty

There's a good explanation of the issue and a fix here gamedev.net/topic/…. It seems that it happens because increasing the angle linearly assumes that the columns cover constant angles but that's not true; the centre column covers a larger angle than the columns on the left/right. It's not completely intuitive to me, but there you go, that seems to be the reason. – Lanni

Thanks, after some further research I've updated my answer above :) – Porty

Thanks! After I wrote that comment I thought more about it and read and re-read the comments in that post, and finally got it. Your diagram also helps! I'm planning on writing a blog post about raycasting soon too so hopefully there'll be more info about it out there :) – Lanni

Answer 2

Having spent a couple of hours trying to solve this exact problem on a raycasting engine of my own, I would like to give more detailed mathematical background as to why this is the correct answer, since I wasn't entirely convinced at first. Especially since when doing perspective projection, you already have to correct some spherical distortion (fish bowl effect). The effect described here is a completely different effect.

This is what I got in my engine: the camera is in a square room, looking at a corner, at an angle of roughly 45°, with a FOV of 90°. It seems to have a slight spherical distortion. The red lines have been added afterward, it is also much more obvious to see in motion, but making a GIF is a PITA:

Spherical distortion

Here is the same room, same location and angle, but with a FOV of 70°. It is not as noticeable (and again, easier to see in motion):

Same room with FOV=70

The first version of my raycasting engine emitted rays from -FOV/2+camera_angle to FOV/2+camera_angle, with each angle spaced by FOV/SCREEN_WIDTH degrees (in my case SCREEN_WIDTH was 640).

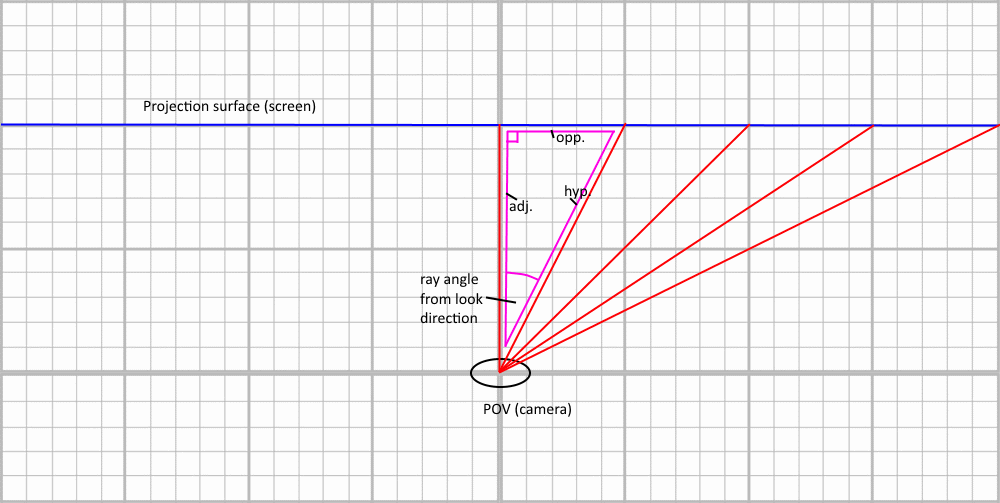
Here is a top-view schema, with SCREEN_WIDTH = 9:

Casting rays

You can see the problem here : when we use a fixed angle, the only thing guaranteed to be constant are those arcs of circle between two rays. But what should be constant are the segments on the projection plane. We can see by using a fixed angle, that the segments get longer the farther from the center.

To solve this, keep in the mind the following parameters :

• FOV = field of view, 90° in this example.
• DIST = distance from camera to projection plane. In my engine I initially choose 50, not knowing better, but it will need to be adjusted depending on the FOV actually.
• SCREEN_WIDTH = width of the screen in pixels, 640 in my example

Knowing this, we can compute what the length of the segments (SEG_LEN) on the projection plane should be, by using some trigonometry in the triangle ABC:

tan(FOV/2) = SCREEN_HALFLEN / DIST

SCREEN_HALFLEN = DIST * tan(FOV/2)

SCREEN_HALFLEN is the length of screen projected on our imaginary plane, to get the SEG_LEN, simply do:

SEG_LEN = SCREEN_HALFLEN / (SCREEN_WIDTH/2)

Knowing the segment length, we can compute the real angles at which rays need to be emitted: given a column x going from 0 to SCREEN_WIDTH-1, the angle should be:

ANGLES[x] = atan(((SEG_LEN * x - SCREEN_HALFLEN) / DIST)

This is the more or less the same formula given by James Hill in his final example. Putting this all together in the engine, it indeed eliminates the spherical distortion:

Spherical distortion corrected

For fun, we can compute what are the differences between a fixed angle raycasting and fixed length raycasting, in the worst case at ray x = 97 where there is a 9 pixels difference:

The angle for the fixed angle raycasting is = 97 * FOV/SCREEN_WIDTH - FOV/2 = -31.359375°

With a fixed length raycasting, the angle is : atan(97 * SEG_LEN / DIST) = -34.871676373193203°

So, up to an 11% error, using given parameters (FOV = 90, DIST = 50, SCREEN_WIDTH = 640).

For reference, I would like to add more detail as to how I implemented this is my engine: for the better or the worse, I wanted to do everything using integer arithmetic (except initialization stuff). First I setup two tables to pre-compute sine and cosine values, using fixed point arithmetic (examples are in C language):

#define FIXEDSHIFT     13
#define FIXEDPRES      (1<<FIXEDSHIFT)
#define DIST           50
#define FOV            90
#define SCREEN_WIDTH   640
#define SCREEN_HEIGHT  480
#define HALF_WIDTH     (SCREEN_WIDTH/2)

int i;
int size = 360.0 / ((double)FOV / SCREEN_WIDTH)));
int16_t * Cos = malloc(size * sizeof *Cos);
int16_t * Sin = malloc(size * sizeof *Sin);

for (i = 0; i < size; i ++)
{
    double angle = i * (2.0*M_PI / size);
    Cos[i] = (int16_t)(cos(angle) * FIXEDPRES);
    Sin[i] = (int16_t)(sin(angle) * FIXEDPRES);
}

I initially used these tables to also cast rays, which resulted in the first 2 screenshots. So I added the ANGLES table, split into cartesian coordinates:

int16_t * XRay = malloc(SCREEN_WIDTH * sizeof *XRay);
int16_t * YRay = malloc(SCREEN_WIDTH * sizeof *YRay);
double    dist = (DIST * tan(FOV*M_PI/360)) / (HALF_WIDTH-1);

for (i = 0; i < HALF_WIDTH; i ++)
{
    #if 0
    /* for fun, this re-enables the spherical distortion */
    double angle = i * (2.0*M_PI / (MAX_TAB));
    #else
    double angle = atan((dist * i) / DIST);
    #endif

    XRay[HALF_WIDTH-i-1] =   XRay[HALF_WIDTH+i] = (int16_t)(cos(angle) * FIXEDPRES);
    YRay[HALF_WIDTH-i-1] = -(YRay[HALF_WIDTH+i] = (int16_t)(sin(angle) * FIXEDPRES));
}

Then in the raycasting engine, to get the correct rays, I used :

int raycasting(int camera_angle)
{
    int i;
    for (i = 0; i < SCREEN_WIDTH; i ++)
    {
        int dx = Cos[camera_angle];
        int dy = Sin[camera_angle];

        /* simply apply a rotation matrix with dx (cos) and dy (sin) */
        int xray = (XRay[i] * dx - YRay[i] * dy) >> FIXEDSHIFT;
        int yray = (XRay[i] * dy + YRay[i] * dx) >> FIXEDSHIFT;

        /* remember that xray and yray are respectively cosine and sine of the current ray */

        /* you will need those values to do perspective projection */

        /* ... */
    }
}

Touristy

Thank you for this answer, after many hours it helped me fix the same issue I had with my raycaster. However I noticed that the fix actually introduces fisheye distortion when using too high FOV (max I can use currently is around 60). Any thoughts on this? Thanks in advance! – Pyrrhonism