Implementing Bron–Kerbosch algorithm in python

Question

for a college project I'm trying to implement the Bron–Kerbosch algorithm, that is, listing all maximal cliques in a given graph.

I'm trying to implement the first algorithm (without pivoting) , but my code doesn't yield all the answers after testing it on the Wikipedia's example , my code so far is :

# dealing with a graph as list of lists 
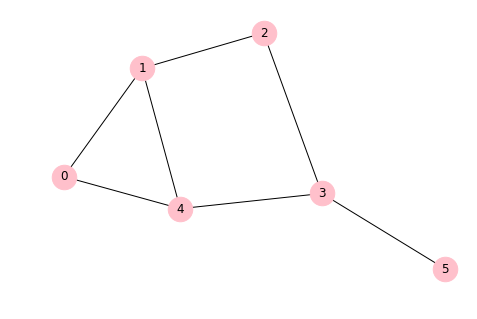
graph = [[0,1,0,0,1,0],[1,0,1,0,1,0],[0,1,0,1,0,0],[0,0,1,0,1,1],[1,1,0,1,0,0],[0,0,0,1,0,0]]


#function determines the neighbors of a given vertex
def N(vertex):
    c = 0
    l = []
    for i in graph[vertex]:
        if i is 1 :
         l.append(c)
        c+=1   
    return l 

#the Bron-Kerbosch recursive algorithm
def bronk(r,p,x):
    if len(p) == 0 and len(x) == 0:
        print r
        return
    for vertex in p:
        r_new = r[::]
        r_new.append(vertex)
        p_new = [val for val in p if val in N(vertex)] # p intersects N(vertex)
        x_new = [val for val in x if val in N(vertex)] # x intersects N(vertex)
        bronk(r_new,p_new,x_new)
        p.remove(vertex)
        x.append(vertex)


    bronk([], [0,1,2,3,4,5], [])

Any help why I'm getting only a part of the answer ?

Aitch

First thing - don't use is for value comparison - that's what == is for – Blowtorch

I would advise against using recursion with side effects (recursion itself is tricky enough to get ones head around!). Also, you could write N using a list comprehension and enumerate. – Manila

Answer 1

Python is getting confused because you are modifying the list that it is iterating over.

Change

for vertex in p:

to

for vertex in p[:]:

this will cause it to iterate over a copy of p instead.

You can read more about this at http://effbot.org/zone/python-list.htm.

Saberio

Thanks very much! that was the problem there. – Aitch

Answer 2

As @VaughnCato correctly points out the error was iterating over P[:]. I thought it worth noting that you can "yield" this result, rather than printing, as follows (in this refactored code):

def bronk2(R, P, X, g):
    if not any((P, X)):
        yield R
    for v in P[:]:
        R_v = R + [v]
        P_v = [v1 for v1 in P if v1 in N(v, g)]
        X_v = [v1 for v1 in X if v1 in N(v, g)]
        for r in bronk2(R_v, P_v, X_v, g):
            yield r
        P.remove(v)
        X.append(v)
def N(v, g):
    return [i for i, n_v in enumerate(g[v]) if n_v]

In [99]: list(bronk2([], range(6), [], graph))
Out[99]: [[0, 1, 4], [1, 2], [2, 3], [3, 4], [3, 5]]

In case someone is looking for a Bron–Kerbosch algorithm implementation in the future...

Manila

I am needing this now. What does enumerate(g[v]) do, can you post your Graph class? – Iphagenia

@DanielDonnelly graph is list of list of 0,1 as in the question. Please ask a new question for more specific questions, I am not sure I can add much to this one. enumerate is in the stdlib. :) – Manila

I think it should be list(bronk2([], [*range(6)], [], graph)) for the function call. – Clare

Answer 3

Implementation of the Bron-Kerbosch Algorithm from Wikipedia:

Without pivoting

algorithm BronKerbosch1(R, P, X) is
    if P and X are both empty then:
        report R as a maximal clique
    for each vertex v in P do
        BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
        P := P \ {v}
        X := X ⋃ {v}

adj_matrix = [
    [0, 1, 0, 0, 1, 0],
    [1, 0, 1, 0, 1, 0],
    [0, 1, 0, 1, 0, 0],
    [0, 0, 1, 0, 1, 1],
    [1, 1, 0, 1, 0, 0],
    [0, 0, 0, 1, 0, 0]]

N = {
    i: set(num for num, j in enumerate(row) if j)
    for i, row in enumerate(adj_matrix)
}

print(N)
# {0: {1, 4}, 1: {0, 2, 4}, 2: {1, 3}, 3: {2, 4, 5}, 4: {0, 1, 3}, 5: {3}}

def BronKerbosch1(P, R=None, X=None):
    P = set(P)
    R = set() if R is None else R
    X = set() if X is None else X
    if not P and not X:
        yield R
    while P:
        v = P.pop()
        yield from BronKerbosch1(
            P=P.intersection(N[v]), R=R.union([v]), X=X.intersection(N[v]))
        X.add(v)

P = N.keys()
print(list(BronKerbosch1(P)))
# [{0, 1, 4}, {1, 2}, {2, 3}, {3, 4}, {3, 5}]

With pivoting

algorithm BronKerbosch2(R, P, X) is
    if P and X are both empty then
        report R as a maximal clique
    choose a pivot vertex u in P ⋃ X
    for each vertex v in P \ N(u):
        BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
        P := P \ {v}
        X := X ⋃ {v}

---

import random  

def BronKerbosch2(P, R=None, X=None):
    P = set(P)
    R = set() if R is None else R
    X = set() if X is None else X
    if not P and not X:
        yield R
    try:
        u = random.choice(list(P.union(X)))
        S = P.difference(N[u])
    # if union of P and X is empty
    except IndexError:
        S = P
    for v in S:
        yield from BronKerbosch2(
            P=P.intersection(N[v]), R=R.union([v]), X=X.intersection(N[v]))
        P.remove(v)
        X.add(v)
  
print(list(BronKerbosch2(P)))
# [{0, 1, 4}, {1, 2}, {2, 3}, {3, 4}, {3, 5}]

Cibis

This set based implementation is both orders of magnitude faster than the list based version and clearer to relate back to the wikipedia pseudocode – Dandiprat