Gaussian smoothing is a common image processing function, and for an introduction of Gaussian filtering, please refer to here. As we can see, one parameter: standard derivation will determine the shape of Gaussian function. However, when we perform convolution with Gaussian filtering, another parameter: the window size of Gaussian filter should also be determined at the same time. For example, when we use fspecial function provided by MATLAB, not only the standard derivation but also the window size must be provided. Intuitively, the larger the Gaussian standard derivation is the bigger the Gaussian kernel window should. However, there is no general rule about how to set the right window size. Any ideas? Thanks!
The size of the mask drives the filter amount. A larger size, corresponding to a larger convolution mask, will generally result in a greater degree of filtering. As a kinda trade-off for greater amounts of noise reduction, larger filters also affect the details quality of the image.
That's as milestone. Now coming to the Gaussian filter, the standard deviation is the main parameter. If you use a 2D filter, at the edge of the mask you will probably desire the weights to approximate 0.
To this respect, as I already said, you can choose a mask with a size which is generally three times the standard deviation. This way, almost the whole Gaussian bell is taken into account and at the mask's edges your weights will asymptotically tend to zero.
I hope this helps.
Given sigma and the minimal weight epsilon in the filter you can solve for the necessary radius of the filter x:
For example if sigma = 1 then the gaussian is greater than epsilon = 0.01 when x <= 2.715 so a filter radius = 3 (width = 2*3 + 1 = 7) is sufficient.
- sigma = 0.5, x <= 1.48, use radius 2
- sigma = 1, x <= 2.715, use radius 3
- sigma = 1.5, x <= 3.84, use radius 4
- sigma = 2, x <= 4.89, use radius 5
- sigma = 2.5, x <= 5.88, use radius 6
If you reduce/increase epsilon then you will need a larger/smaller radius.
Here is a good reference.
After discretizing, pixel with distance greater than 3 sigma have negligible weights. See this
As already pointed, 6sigma, implies 3sigma both ways
Size of convolution matrix to be used for filtering would inadvertently be 6sigma by 6sigma, because of points 1 and 2 above.
Here how you can obtain the discrete Gaussian.
Finally, the size of the standard deviation(and therefore the Kernel used) depends on how much noise you suspect to be in the image. Clearly, a larger convolution kernel implies farther pixels get to contribute to the new value of the centre pixel as opposed to a smaller kernel.
© 2022 - 2024 — McMap. All rights reserved.

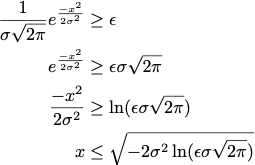
sizewhich is at least 3 times the selectedstandard deviationof your Gaussianbell. – Discriminating