The interpolate method expects arrays of pairs (here called x and y) and returns a function (psf) that fits these values as best as possible.
This function is then used to interpolate the yi-value of a given xi-value (which is normally not contained in the x/y array used to define the function).
So you have pairs containing of x- and y-values defining a function and use this function to interpolate missing values.
See the userguide on Apache Commons (Chapter 4.4: Interpolation).
Example:
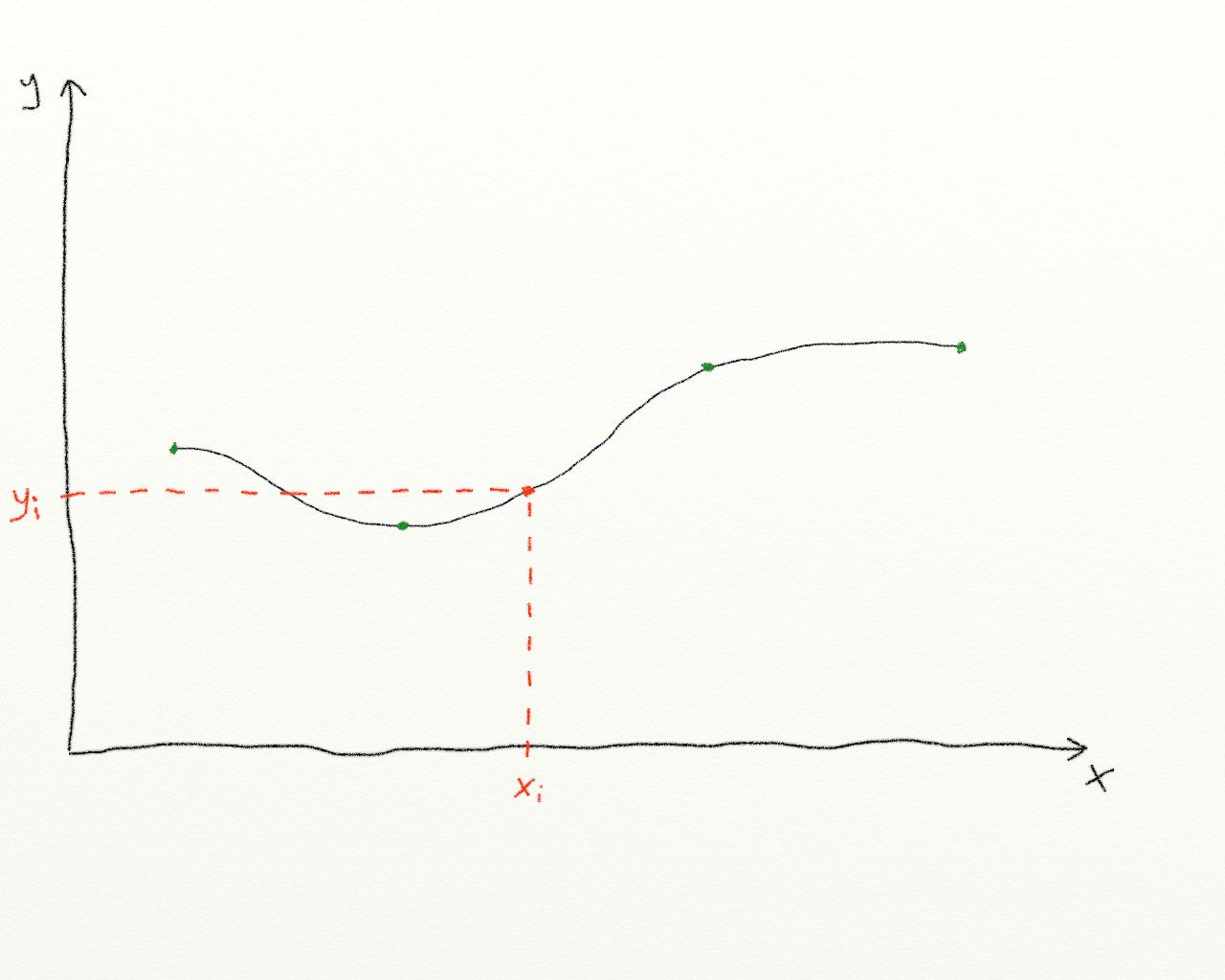
![badly drawn example of a spline interpolation]()
The green dots are known value pairs. These are defined by the x and y value arrays.
When calling interpolate, the returned PolynomialSplineFunction returns the function that is approximated using the known value pairs. The shape of the funtion is defined by the type of UnivariateInterpolator that is used. In the question example, a LinearInterpolator is used. The drawing shows the function returned by a spline interpolator.
The red dot symbolizes a value with an unknown y-value on the interpolated function (this would be the value with an x-value of xi in the question example).
If you need to calculate more than one extra value, use a function like this
public double[] linearInterp(double[] x, double[] y, double[] xi) {
LinearInterpolator li = new LinearInterpolator(); // or other interpolator
PolynomialSplineFunction psf = li.interpolate(x, y);
double[] yi = new double[xi.length];
for (int i = 0; i < xi.length; i++) {
yi[i] = psf.value(xi[i]);
}
return yi;
}
A calculation example:
public class Interpolate {
public static void main(String[] args) {
double[] x = { 0, 50, 100 };
double[] y = { 0, 50, 200 };
LinearInterpolator interp = new LinearInterpolator();
PolynomialSplineFunction f = interp.interpolate(x, y);
System.out.println("Piecewise functions:");
Arrays.stream(f.getPolynomials()).forEach(System.out::println);
double value = f.value(70);
System.out.println("y for xi = 70: " + value);
}
}
Three known value pairs are given:
(0, 0)
(50, 50)
(100, 200)
One value is unknown:
(70, ?)
The LinearInterpolator interpolates the given values and generates a function with two piecewise, linear polynomials:
y = x (for x values < 50)
y = 50 + 3 * x (for x-values >= 50)
The value of the interpolated xi (here: 70) is
y = 50 + 3 * (70 - 50) = 110

highchart.jsto plot the data. My ultimate goal is to have an extrapolation function to plot points in the future using the using my set of X/Y points. maybe using something like this: https://mcmap.net/q/1322911/-extrapolation-in-java But I've been led to believe if I have an interpolation function, I can use that function to extrapolate. – Changeable