Why does MATLAB's element-wise exponentiation speed up for 512 elements?

Question

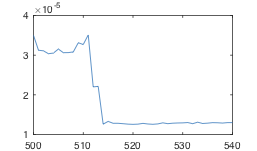
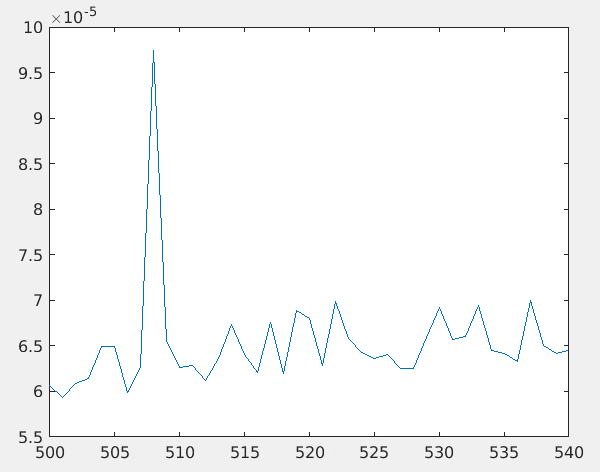
MATLAB's power function to calculate element-wise exponential for a constant base and an array of exponents becomes noticeably faster when the size of the array becomes 512. I expected to see the computation time increase with the input size, however, there is a noticeable drop when there are 512 elements in the array of exponents. Here is a sample code

x_list = 510:514;
for i = 1:numel(x_list)
    x = x_list(i);
    tic
    for j = 1:10000
        y = power(2,1:x); 
    end
    toc
end

The output of the code is

Elapsed time is 0.397649 seconds.
Elapsed time is 0.403687 seconds.
Elapsed time is 0.318293 seconds.
Elapsed time is 0.238875 seconds.
Elapsed time is 0.175525 seconds.

What is happening here?

Caputo

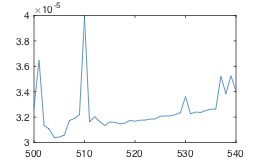
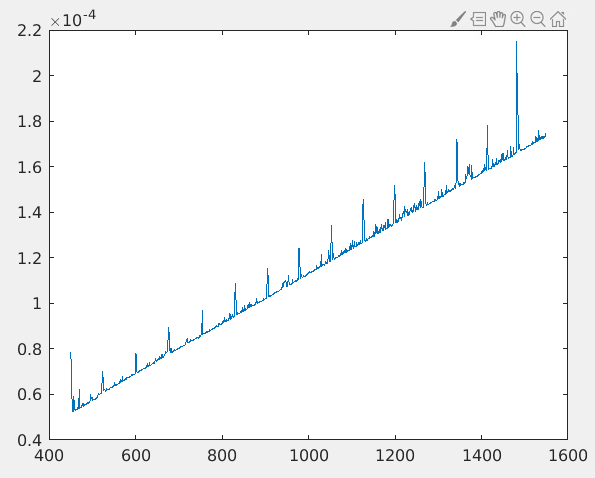
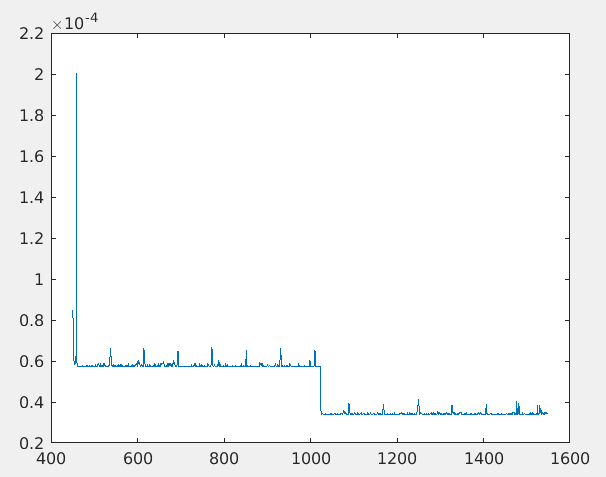
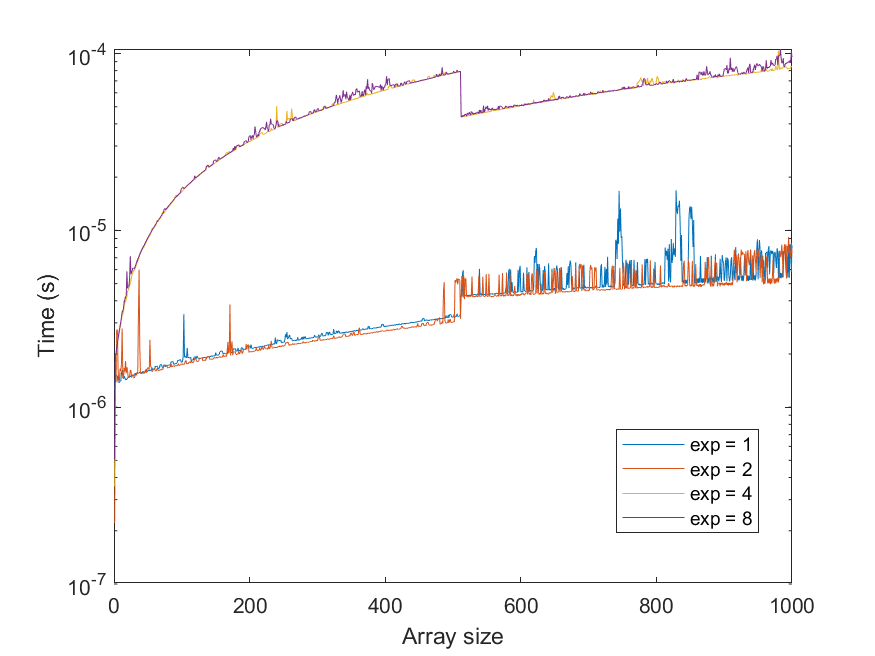
Note that tic/toc is not recommended when doing accurate timings; instead, use timeit(), which has been designed to accurately assess performance. Otherwise, I think this has to do with the implementation of FFTW, which also uses a trick to compute very fast on sizes of 2^n, although I'd expect a speed-up for 1024 and 2048 elments then as well. – Livelihood

@Livelihood I was able to reproduce the graph with timeit. – Sayed

I've timed the function for arrays of exponents of size up to 2^16 but it does not show any speedup around powers of 2 the way it does around an array of exponents with 2^9 elements. – Caputo

Answer 1

I see the same effect using random numbers for the exponent, as I see using integers in the range 1:n:

x = 500:540;
t = zeros(size(x));
for ii = 1:numel(x)
    %m = 1:x(ii);
    m = 500*rand(1,x(ii));
    t(ii) = timeit(@()power(2,m));
end
plot(x,t)

When forcing MATLAB to use a single thread with maxNumCompThreads(1), and running the code above again, I see this graph instead (note the y-axis, the peaks are just noise):

It looks to me that MATLAB uses a single core to compute the exponent of 511 values, and fires up all cores if the matrix is larger. There is an overhead in using multithreading, it is not worth while to do so for small arrays. The exact point where the overhead is balanced by the time savings depends on many factors, and so hard-coding a fixed threshold for when to switch to multithreaded computation leads to a jump in execution time on systems with different characteristics to those of the system where the threshold was determined.

Note that @norok2 is not seeing this same jump because on their system MATLAB was limited to a single thread.

Delija

[Completely untested suggestion] - maybe you could use explicit multithreading to test this theory: undocumentedmatlab.com/blog/… – Raynold

Nice one :) Makes sense to me! – Raynold

@CrisLuengo The reason why I was not able to reproduce this graph was that the admin set it up to have single thread computations. Upvoted. – Rawson

Answer 2

This is related to size of the number for which the power is computed rather than the size of the container.

If you use random numbers, for varying container size, one does not observe a jump in the timings:

x = 450:1550;
y = zeros(numel(x), 1);
X = rand(1, 10000);
for i = 1:length(x)
    f = @() 2 .^ X(1:x(i));
    y(i) = timeit(f);
end

figure()
plot(x, y)

Therefore the issue must be with the computation for very large numbers. I first I thought that this might be related to overflow, but the overflow happens at 2 ^ 1024 == inf as dictated by the IEEE standards which MATLAB follows, and I thought that for inf this is would have been much faster than computing a number for real.

This is supported by the following benchmark where the size of the array is kept constant:

x = 450:1550;
y = zeros(numel(x), 1);
X = rand(1, 10000);
for i = 1:length(x)
    f = @() 2 .^ (ones(1, 500) * x(i));
    y(i) = timeit(f);
end

figure()
plot(x, y)

Why exactly this may be relevant for your setup when 2 ^ 512 instead of 2 ^ 1024, I do not really understand.

(Note that I used 2 .^ ... instead of power(2, ...) but the results are the same.)

---

Also, running @CrisLuengo's code in my system does not really reproduce any jump.

x = 500:540;
t = zeros(size(x));
for ii = 1:numel(x)
    %m = 1:x(ii);
    m = 500*rand(1,x(ii));
    t(ii) = timeit(@()power(2,m));
end
plot(x,t)

all the evidence so far indicate that spike being a related to JIT latency/warm-up.

Rawson

So nobody can reproduce my graphs? I must have a very special version of MATLAB... – Rawson

Strange that you cannot reproduce the jump. I'm reversing my downvote. I'm going to try to reproduce your graphs, but earlier I didn't notice any difference with the magnitude of the exponent. What OS are you using? What version of MATLAB? How many cores do you have? I used a 4-core iMac and R2017a. – Delija

I am running on a HPC. I have reserved 4 cores from an Intel Xeon E5-2680 v4 cluster, 3 GB of memory, MATLAB R2018b. – Rawson

OK, I can reproduce your jump at 1024. And actually, you not seeing the jump at 512 makes me think that my proposed reason might be right: your system has similar properties to the one that the guys at MathWorks used to determine the threshold, whereas mine and OP's don't. – Delija

To add my 2c, I get exactly the same plot as your first test (step down at 1024), but I also get a significant step down after 512 in the 2nd plot (after a similar spike at 512). The plot thickens. – Raynold

@CrisLuengo as far as I understand, you are proposing the jump to happen for some array size, but my benchmarks suggest the jumps happening depending on the values of the array, not their size. – Rawson

@CrisLuengo OP graph goes up to 10000. Yet, I think you are right that the effect may be dominated by multithreading kicking in. I double-checked and the sysadmin limited MATLAB to run in single-thread mode, so I am out of help to further test your hypothesis. – Rawson

Yes, you're right, OP's graph goes way up. I guess there's no jump there to be seen there because that code doesn't make all exponents the same, it adds values above the limit. So your answer explains why the graph flattens out above 1024. – Delija

Answer 3

Here's some confirmation of what Cris found, using a 4-core Windows machine running MATLAB R2018a. I first tested the following code to show that the specific value of the exponent wasn't the culprit for the jump:

t = zeros(4, 1000);
for p = 1:size(t, 1)
  for n = 1:size(t, 2)
    t(p, n) = timeit(@() power(2, (2.^(p-1)).*ones(1, n)));
  end
end

And here are the results:

For degenerate edge cases where the exponent is 1 (return the same value) or 2 (return the value times itself) the computation runs faster, as expected. However, the jump at an array size of 512 or above indicates overhead is added to these edge cases, compared to a reduction in computation time for exponents of 4 and 8 when the array size exceeds 512. Larger exponent values simply reproduce the upper curves.

I then ran two more tests: one with array size between 1 and 511, and a second with array size between 512 and 1024. Here's what the processor load looked like:

Processor 3 shows a large load spike during the first test, while all 4 processors show load spikes during the second test. This confirms that multithreading is employed for array sizes of 512 or above. This also explains the slower computation for edge cases of larger sizes, since the overhead from multithreading outweighs the speedup provided by splitting up the simpler calculations.

Sayed