create cosine similarity matrix numpy

Question

Suppose I have a numpy matrix like the following:

array([array([ 0.0072427 ,  0.00669255,  0.00785213,  0.00845336,  0.01042869]),
   array([ 0.00710799,  0.00668831,  0.00772334,  0.00777796,  0.01049965]),
   array([ 0.00741872,  0.00650899,  0.00772273,  0.00729002,  0.00919407]),
   array([ 0.00717589,  0.00627021,  0.0069514 ,  0.0079332 ,  0.01069545]),
   array([ 0.00617369,  0.00590539,  0.00738468,  0.00761699,  0.00886915])], dtype=object)

How can I generate a 5 x 5 matrix where each index of the matrix is the cosine similarity of two corresponding rows in my original matrix?

e.g. row 0 column 2's value would be the cosine similarity between row 1 and row 3 in the original matrix.

Here's what I've tried:

from sklearn.metrics import pairwise_distances
from scipy.spatial.distance import cosine
import numpy as np

#features is a column in my artist_meta data frame
#where each value is a numpy array of 5 floating point values, similar to the
#form of the matrix referenced above but larger in volume

items_mat = np.array(artist_meta['features'].values)

dist_out = 1-pairwise_distances(items_mat, metric="cosine")

The above code gives me the following error:

ValueError: setting an array element with a sequence.

Not sure why I'm getting this because each array is of the same length (5), which I've verified.

Arsonist

What did you try? Show us your code. – Lewallen

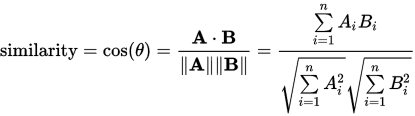
1-pairwise_distances(f,metric="cosine") is doing just what you need, assuming that f is the original array at the top of your post. There may be an issue with the content of items_mat. Can you show the first, say, 5x5 elements of it? – Lewallen

Sure - the matrix in the original post has been updated to reflect the first five rows of the one I am computing. Even on computing the cosine similarity of the first five rows I run into the error. – Arsonist

So, as I said before, assuming that f is your matrix, 1-pairwise_distances(f,metric="cosine") gives no errors whatsoever. – Lewallen

Make sure the array dtype is float and not object – Hemminger

The issue turned out to be that it was an object type - casting the matrix as a list and then back to a matrix fixed it for me! – Arsonist

Answer 1

let m be the array

m = np.array([
        [ 0.0072427 ,  0.00669255,  0.00785213,  0.00845336,  0.01042869],
        [ 0.00710799,  0.00668831,  0.00772334,  0.00777796,  0.01049965],
        [ 0.00741872,  0.00650899,  0.00772273,  0.00729002,  0.00919407],
        [ 0.00717589,  0.00627021,  0.0069514 ,  0.0079332 ,  0.01069545],
        [ 0.00617369,  0.00590539,  0.00738468,  0.00761699,  0.00886915]
    ])

---

per wikipedia: Cosine_Similarity

We can calculate our numerator with

d = m.T @ m

Our ‖A‖ is

norm = (m * m).sum(0, keepdims=True) ** .5

Then the similarities are

d / norm / norm.T

[[ 1.      0.9994  0.9979  0.9973  0.9977]
 [ 0.9994  1.      0.9993  0.9985  0.9981]
 [ 0.9979  0.9993  1.      0.998   0.9958]
 [ 0.9973  0.9985  0.998   1.      0.9985]
 [ 0.9977  0.9981  0.9958  0.9985  1.    ]]

The distances are

1 - d / norm / norm.T

[[ 0.      0.0006  0.0021  0.0027  0.0023]
 [ 0.0006  0.      0.0007  0.0015  0.0019]
 [ 0.0021  0.0007  0.      0.002   0.0042]
 [ 0.0027  0.0015  0.002   0.      0.0015]
 [ 0.0023  0.0019  0.0042  0.0015  0.    ]]

Malia

To optimize your code, you can divide m by norm once before doing m.T @ m. It saves the division by norm.T. – Ape

I agree with @IsmaelELATIFI. The optimized code is: norm = (m * m).sum(0, keepdims=True) ** .5; m_norm = m/norm; similarity_matrix = m_norm.T @ m_norm – Cynic

Just to add ^^. When you have unit vectors, the cosine distance is the same as just the dot product. – Valora

Shouldn't it be m @ m.T ? If I have an M x N matrix, so M vectors each of it N-dimensional, I want to have an M x M distance matrix. [M x N] @ [N x M] = [M x M]. – Teacher

per formulae, d / (norm * norm.T) ? – Charmainecharmane

Right. It should be Norm @ Norm.T. Also, technically the sum should use axis=1 so that it sums across each row (not column). I've added all of this together into a one, tested answer against existing implementations. Of course, the pairwise version also works fine. – Uncompromising

Answer 2

Let x be your array

from scipy.spatial.distance import cosine

m, n = x.shape
distances = np.zeros((m,n))
for i in range(m):
    for j in range(n):
        distances[i,j] = cosine(x[i,:],x[:,j])

Melanymelaphyre

Answer 3

As mentioned, you can use the pairwise function from sklearn. Here is a full implementation as well as verification that it matches the sklearn and scipy versions. I use rounding to 4 decimal places for this example.

import numpy as np
from scipy.spatial.distance import cosine
from sklearn.metrics import pairwise_distances

def cosine_distance_matrix(column: pd.Series, decimals: int = 4):
    """
    Calculate cosine distance of column against itself (pairwise)
    
    Args:
        column:
            pandas series containing np.array values
        decimals:
            how many places to round the output
            
    Returns:
        distance matrix of shape (len(column), len(column))
    """
    M = np.vstack(column.values)
    
    # Perform division by magnitude of pairs first
    # M / (||A|| * ||B||)
    M_norm = M / np.sqrt(np.square(M).sum(1, keepdims=True))
    
    # Perform dot product
    similarity = M_norm @ M_norm.T
    
    # Convert from similarity to distance
    return (1 - similarity).round(decimals)

# Example for testing
sample_column = pd.Series([
    np.array([3, 4]),
    np.array([7, 24]),
    np.array([1, 1])
])

# Try our own fast implementation
custom_version = cosine_distance_matrix(sample_column, decimals=4)

# Use pairwise function from sklearn
pairwise_version = pairwise_distances(
    np.vstack(sample_column.values),
    metric="cosine"
).round(4)

# Equals pairwise version
assert (custom_version == pairwise_version).all()

# Check single element
assert custom_version[0, 1] == cosine(sample_column[0], sample_column[1]).round(4)

Uncompromising