Parallel running of Racket code for N-Queens problem

To start, before even parallelizing anything, you can improve your original program quite a bit. Here are some changes you can make:

Use for/or instead of mutating a binding and using #:break.
Use for*/or instead of nesting for/or loops inside of each other.
Use in-range where possible to ensure for loops specialize to simple loops upon expansion.
Use square brackets instead of parentheses in the relevant places to make your code more readable to Racketeers (especially since this code isn’t remotely portable Scheme, anyway).

With those changes, the code looks like this:

#lang racket

; following returns true if queens are on diagonals:  
(define (check-diagonals bd) 
  (for*/or ([r1 (in-range (length bd))]
            [r2 (in-range (add1 r1) (length bd))])
    (= (abs (- r1 r2))
       (abs (- (list-ref bd r1)
               (list-ref bd r2))))))

; set board size: 
(define N 8)
; start searching: 
(for ([brd (in-permutations (range N))])
  (unless (check-diagonals brd)
    (displayln brd)))

Now we can turn to parallelizing. Here’s the thing: parallelizing things tends to be tricky. Scheduling work in parallel tends to have overhead, and that overhead can outweigh the benefits more often than you might think. I spent a long time trying to parallelize this code, and ultimately, I was not able to produce a program that ran faster than the original, sequential program.

Still, you are likely interested what I did. Maybe you (or someone else) will be able to come up with something better than I can. The relevant tool for the job here is Racket’s futures, designed for fine-grained parallelism. Futures are fairly restrictive due to the way Racket’s runtime is designed (which is essentially the way it is for historical reasons), so not just anything can be parallelized, and a fairly large number of operations can cause futures to block. Fortunately, Racket also ships with the Future Visualizer, a graphical tool for understanding the runtime behavior of futures.

Before we can begin, I ran the sequential version of the program with N=11 and recorded the results.

$ time racket n-queens.rkt
[program output elided]
       14.44 real        13.92 user         0.32 sys

I will use these numbers as a point of comparison for the remainder of this answer.

To start, we can try replacing the primary for loop with for/asnyc, which runs all its bodies in parallel. This is an extremely simple transformation, and it leaves us with the following loop:

(for/async ([brd (in-permutations (range N))])
  (unless (check-diagonals brd)
    (displayln brd)))

However, making that change does not improve performance at all; in fact, it significantly reduces it. Merely running this version with N=9 takes ~6.5 seconds; with N=10, it takes ~55.

This is, however, not too surprising. Running the code with the futures visualizer (using N=7) indicates that displayln is not legal from within a future, preventing any parallel execution from ever actually taking place. Presumably, we can fix this by creating futures that just compute the results, then print them serially:

(define results-futures
  (for/list ([brd (in-permutations (range N))])
    (future (λ () (cons (check-diagonals brd) brd)))))

(for ([result-future (in-list results-futures)])
  (let ([result (touch result-future)])
    (unless (car result)
      (displayln (cdr result)))))

With this change, we get a small speedup over the naïve attempt with for/async, but we’re still far slower than the sequential version. Now, with N=9, it takes ~4.58 seconds, and with N=10, it takes ~44.

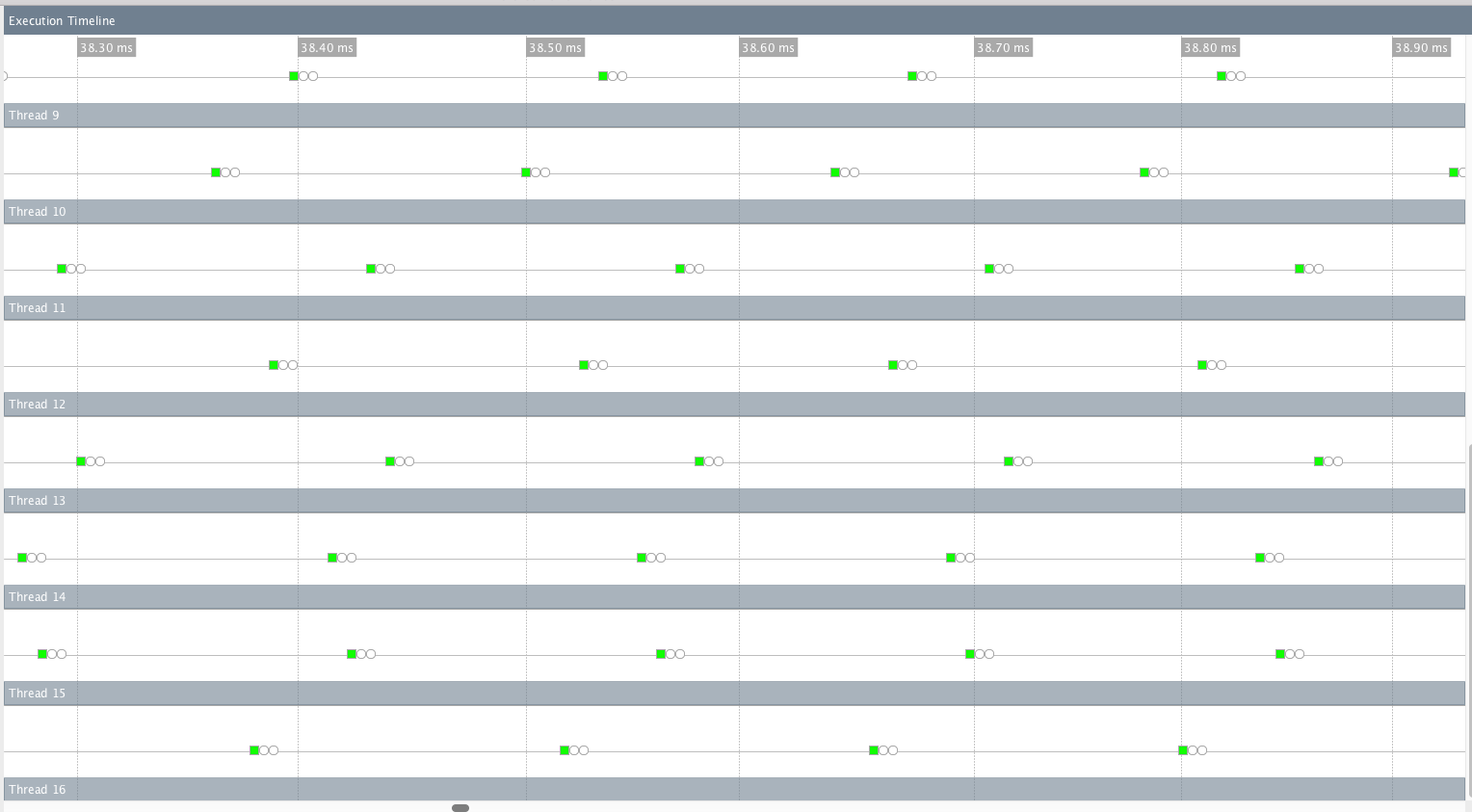
Taking a look at the futures visualizer for this program (again, with N=7), there are now no blocks, but there are some syncs (on jit_on_demand and allocate memory). However, after some time spent jitting, execution seems to get going, and it actually runs a lot of futures in parallel!

After a little bit of that, however, the parallel execution seems to run out of steam, and things seem to start running relatively sequentially again.

I wasn’t really sure what was going on here, but I thought maybe it was because some of the futures are just too small. It seems possible that the overhead of scheduling thousands of futures (or, in the case of N=10, millions) was far outweighing the actual runtime of the work being done in the futures. Fortunately, this seems like something that could be solved by just grouping the work into chunks, something that’s relatively doable using in-slice:

(define results-futures
  (for/list ([brds (in-slice 10000 (in-permutations (range N)))])
    (future
     (λ ()
       (for/list ([brd (in-list brds)])
         (cons (check-diagonals brd) brd))))))

(for* ([results-future (in-list results-futures)]
       [result (in-list (touch results-future))])
  (unless (car result)
    (displayln (cdr result))))

It seems that my suspicion was correct, because that change helps a whole lot. Now, running the parallel version of the program only takes ~3.9 seconds for N=10, a speedup of more than a factor of 10 over the previous version using futures. However, unfortunately, that’s still slower than the completely sequential version, which only takes ~1.4 seconds. Increasing N to 11 makes the parallel version take ~44 seconds, and if the chunk size provided to in-slice is increased to 100,000, it takes even longer, ~55 seconds.

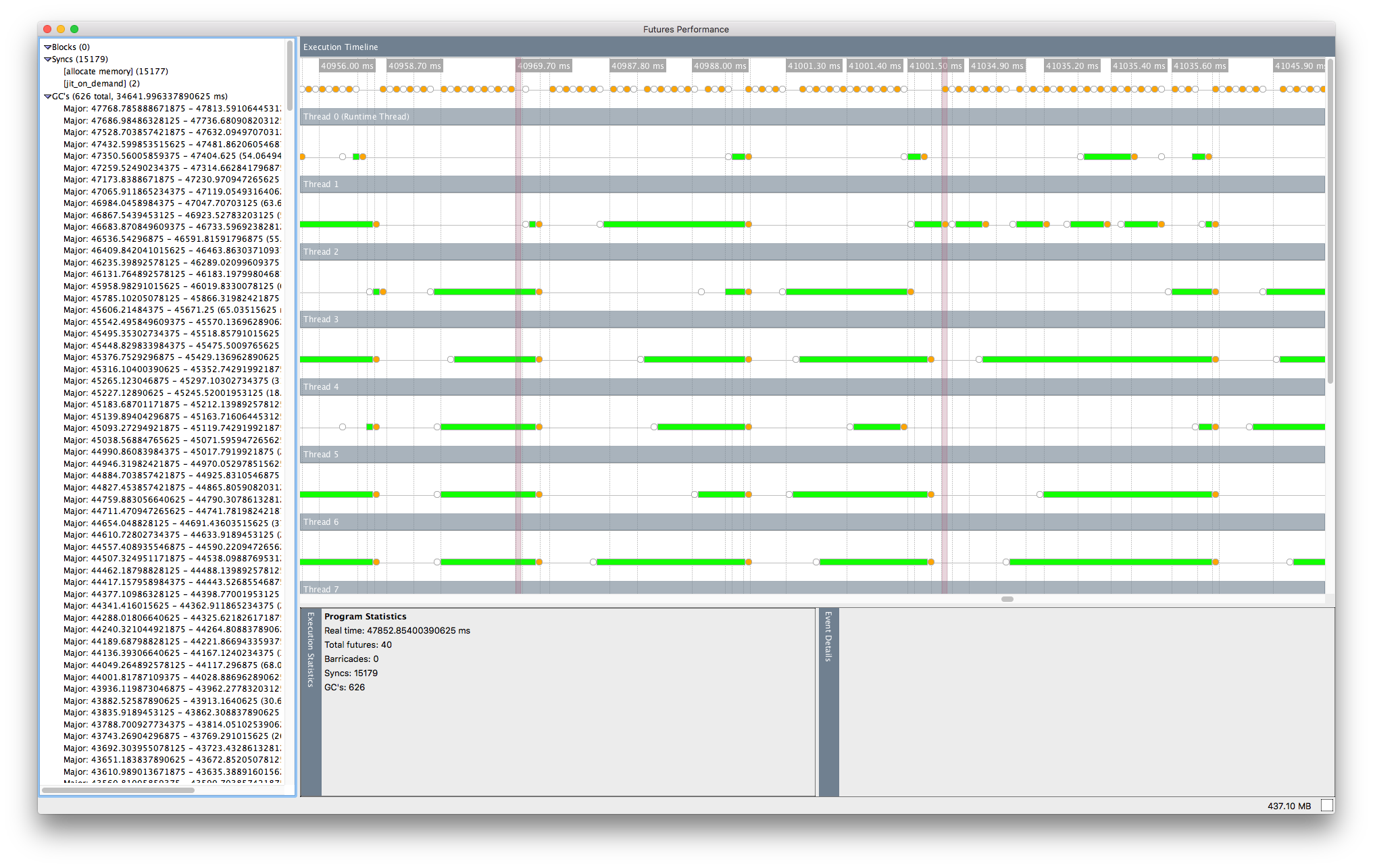
Taking a look at the future visualizer for that version of the program, with N=11 and a chunk size of 1,000,000, I see that there seem to be some periods of extended parallelism, but the futures get blocked a lot on memory allocation:

This makes sense, since now each future is handling much more work, but it means the futures are synchronizing constantly, likely leading to the significant performance overhead I’m seeing.

At this point, I’m not sure there’s much else I know how to tweak to improve future performance. I tried cutting down allocation by using vectors instead of lists and specialized fixnum operations, but for whatever reason, that seemed to completely destroy parallelism. I thought that maybe that was because the futures were never starting up in parallel, so I replaced future with would-be-future, but the results were confusing to me, and I didn’t really understand what they meant.

My conclusion is that Racket’s futures are simply too fragile to work with this problem, simple as it may be. I give up.

Now, as a little bonus, I decided to try and emulate the same thing in Haskell, since Haskell has a particularly robust story for fine-grained parallel evaluation. If I couldn’t get a performance boost in Haskell, I wouldn’t expect to be able to get one in Racket, either.

I’ll skip all the details about the different things I tried, but eventually, I ended up with the following program:

import Data.List (permutations)
import Data.Maybe (catMaybes)

checkDiagonals :: [Int] -> Bool
checkDiagonals bd =
  or $ flip map [0 .. length bd - 1] $ \r1 ->
    or $ flip map [r1 + 1 .. length bd - 1] $ \r2 ->
      abs (r1 - r2) == abs ((bd !! r1) - (bd !! r2))

n :: Int
n = 11

main :: IO ()
main =
  let results = flip map (permutations [0 .. n-1]) $ \brd ->
        if checkDiagonals brd then Nothing else Just brd
  in mapM_ print (catMaybes results)

I was able to easily add some parallelism using the Control.Parallel.Strategies library. I added a line to the main function that introduced some parallel evaluation:

import Control.Parallel.Strategies
import Data.List.Split (chunksOf)

main :: IO ()
main =
  let results =
        concat . withStrategy (parBuffer 10 rdeepseq) . chunksOf 100 $
        flip map (permutations [0 .. n-1]) $ \brd ->
          if checkDiagonals brd then Nothing else Just brd
  in mapM_ print (catMaybes results)

It took some time to figure out the right chunk and rolling buffer sizes, but these values gave me a consistent 30-40% speedup over the original, sequential program.

Now, obviously, Haskell’s runtime is considerably more suited for parallel programming than Racket’s, so this comparison is hardly fair. But it helped me to see for myself that, despite having 4 cores (8 with hyperthreading) at my disposal, I wasn’t able to get even a 50% speedup. Keep that in mind.

As Matthias noted in a mailing list thread I wrote on this subject:

A word of caution on parallelism in general. Not too long ago, someone in CS at an Ivy League school studied the use of parallelism across different uses and applications. The goal was to find out how much the ‘hype’ about parallelism affected people. My recollection is that they found close to 20 projects where professors (in CE, EE, CS, Bio, Econ, etc) told their grad students/PhDs to use parallelism to run programs faster. They checked all of them and for N - 1 or 2, the projects ran faster once the parallelism was removed. Significantly faster.

People routinely underestimate the communication cost that parallelism introduces.

Be careful not to make the same mistake.

Recommended topics

Hot tags