`Optimal` variable initialization and learning rate in Tensorflow for matrix factorization

Question

I'm trying a very simple optimization in Tensorflow- the problem of matrix factorization. Given a matrix V (m X n), decompose it into W (m X r) and H (r X n). I'm borrowing a gradient descent based tensorflow based implementation for matrix factorization from here.

Details about the matrix V. In its original form, the histogram of entries would be as follows:

To bring the entries on a scale of [0, 1], I perform the following preprocessing.

f(x) = f(x)-min(V)/(max(V)-min(V))

After normalization, the histogram of data would look like the following:

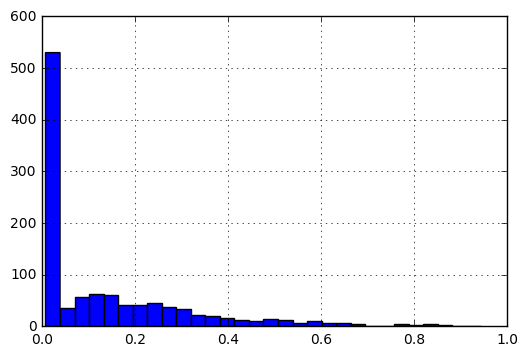
My questions are:

1. Given the nature of data: between 0 and 1 and most entries closer to 0 than 1, what would be the optimal initialisation for W and H?
2. How should the learning rates be defined based on different cost function: |A-WH|_F and |(A-WH)/A|?

The minimal working example would be as follows:

import tensorflow as tf
import numpy as np
import pandas as pd

V_df = pd.DataFrame([[3, 4, 5, 2],
               [4, 4, 3, 3],
               [5, 5, 4, 4]], dtype=np.float32).T

Thus, V_df looks like:

    0   1   2
0   3.0 4.0 5.0
1   4.0 4.0 5.0
2   5.0 3.0 4.0
3   2.0 3.0 4.0

Now, the code defining W, H

V = tf.constant(V_df.values)
shape = V_df.shape
rank = 2 #latent factors

initializer = tf.random_normal_initializer(mean=V_df.mean().mean()/5,stddev=0.1 )
#initializer = tf.random_uniform_initializer(maxval=V_df.max().max())

H =  tf.get_variable("H", [rank, shape[1]],
                                 initializer=initializer)
W =  tf.get_variable(name="W", shape=[shape[0], rank],
                                 initializer=initializer)
WH = tf.matmul(W, H)

Defining the cost and optimizer:

f_norm = tf.reduce_sum(tf.pow(V - WH, 2))
lr = 0.01
optimize = tf.train.AdagradOptimizer(lr).minimize(f_norm)

Running the session:

max_iter=10000
display_step = 50

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())

    for i in xrange(max_iter):

        loss, _ = sess.run([f_norm, optimize])
        if i%display_step==0:
            print loss, i
    W_out = sess.run(W)
    H_out = sess.run(H)
    WH_out = sess.run(WH)

I realized that when I used something like initializer = tf.random_uniform_initializer(maxval=V_df.max().max()), I got matrices W and H such that their product was much greater than V. I also realised that keeping learning rate (lr) to be .0001 was probably too slow.

I was wondering if there are any rules of thumb for defining good initializations and learning rate for the problem of matrix factorization.

Gothic

The question is very well exposed, but I.M.O. this is off-topic. Tuning parameters, like learning rate and initialization matrices, typically depends on the problem being addressed, and you will not get better opinions than those provided in the optimizer documentation. – Nankeen

@rll: I understand your point. I have thus edited the question and provided more details about the exact nature of data involved in this problem. I think such settings can be fairly common (data normalised between 0 and 1) – Gothic

I agree with rll - optimal learning rates and initialization matrices greatly depend on your data/problem statement and often require manual tuning to get the best performance out of your model. By the way, in the code example you linked, they are solving non-negative matrix factorization. Do you also have this constraint on W and/or H or can W and H be arbitrary matrices? – Disproportion

@kaufmanu both W and H also need to be non-negative – Gothic

Answer 1

I think the choice of learning rate is an empirical issue of trial and error, unless you device a second algorithm to find optimal values. It is also a practical concern depending on how much time you have for the computation to finish - given the computing resources that you have available.

However, one should be careful when setting initialization and learning rates as some values will never converge, depending on the machine learning problem. One rule of thumb is to manually change the magnitude in steps of 3 and not 10 (according to Andrew Ng): instead of moving from 0.1 to 1.0, you would go from 0.1 to 0.3.

For your specific data which features multiple values near 0, it is possible to find optimal initialization values given the specific "hypothesis"/model. However, you need to define "optimal". Should the method be as fast as possible, as accurate as possible, or some midpoint between these extremes? (Accuracy is not always a problem when seeking exact solutions. When it is, however, the choice of stopping rule and the criteria for reducing errors can affect the outcome.)

Even if you do find optimal parameters for this set of data, you might have problems using the same formula for other data sets. If you wish to use the same parameters for a different problem, you will loose generalizability, unless you have strong reasons to expect other data sets to follow a similar distribution.

For the specific algorithm at hand, which uses a stochastic gradient decent there appears to be no simple answers*. The TensorFlow documentation refers to two sources:

• The AdaGrad algorithm (includes evaluation of its performance)

  http://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf

• An introduction to convex optimization

  http://cs.stanford.edu/~ppasupat/a9online/uploads/proximal_notes.pdf

_{* "It is hopefully clear that choosing a good matrix B in the update ... can substantially improve the standard gradient method ... Often, however, such a choice is not obvious, and in stochastic settings... it is highly non-obvious how to choose this matrix. Moreover, in many stochastic settings, we do not even know the true function we are minimizing, since data simply arrives in a stream, so pre-computing a good distance-generating matrix is impossible." Duchi & Singer, 2013, p. 5}

Scourge